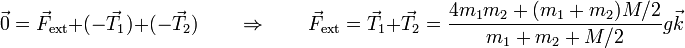Máquina de Atwood con polea pesada

De Laplace

Contenido

1 Enunciado
2 Aceleración
3 Tensiones
4 Fuerza en el soporte

1 Enunciado

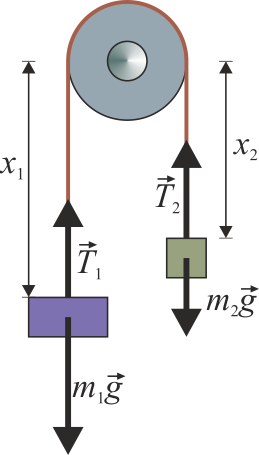
Dos masas $m 1$ y $m 2$ están unidas por una cuerda ideal, inextensible y sin masa. Esta cuerda pasa por una polea de masa $M$ , que se puede modelar como un cilindro de radio $R$ . La polea no tiene rozamiento que le impida girar en torno a su eje. Determine la aceleración con la que se mueven las masas, las tensiones en cada tramo de la cuerda, así como la fuerza en el punto de anclaje de la polea.

2 Aceleración

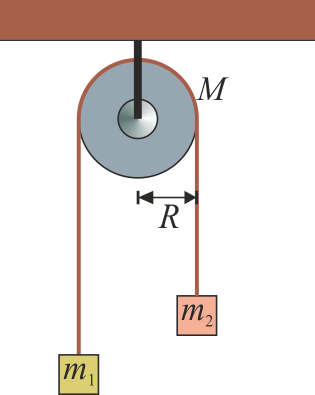
Usando la misma notación que en el tema de dinámica de la partícula consideramos que cada masa se mueve verticalmente, por lo que podemos usar cantidades escalares.

En este caso, la ecuación de movimiento para cada una de las masas queda

$m_1a = -m_1g+T_1\qquad\qquad -m_2a = -m_2 g + T_2$

Sigue siendo cierto que la aceleración con la que sube la masa 1 coincide con la que baja la masa 2, pero ya no es cierto que la tensión de la cuerda sea la misma en el lado de la masa 1 que en el de la masa 2. La razón es que es la diferencia entre esas dos tensiones la que hace girar la polea. Si las dos tensiones fueran iguales su par se cancelaría y no habría rotación alguna.

La ecuación de movimiento para la rotación de la polea es, por tratarse de una rotación en torno a un eje de simetría que pasa por el CM del sólido

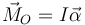
$\vec{M}_O = I\vec{\alpha}$

donde el momento de las fuerzas vale

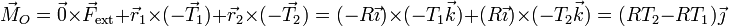
$\vec{M}_O = \vec{0}\times\vec{F}_\mathrm{ext}+\vec{r}_1\times(-\vec{T}_1)+\vec{r}_2\times(-\vec{T}_2) =(-R\vec{\imath})\times(-T_1\vec{k})+(R\vec{\imath})\times(-T_2\vec{k})=(RT_2-RT_1)\vec{\jmath}$

el momento de inercia es

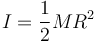
$I = \frac{1}{2}MR^2$

y la aceleración angular, teniendo en cuenta que la polea gira en contacto con la cuerda

$\alpha = \frac{a}{R}\qquad\qquad \vec{\alpha}=\frac{a}{R}\vec{\jmath}$

Sustituyendo esto nos queda la ecuación escalar

$RT_2-RT_1 = \frac{1}{2}MR^2\frac{a}{R}\qquad\Rightarrow\qquad T_2 - T_1 = \frac{Ma}{2}$

Despejando las tensiones de las ecuaciones de movimiento para las masas y sustituyendo aquí

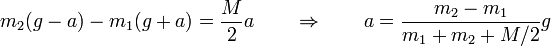
$m_2(g-a) -m_1(g+a) = \frac{M}{2}a\qquad \Rightarrow\qquad a = \frac{m_2-m_1}{m_1+m_2+M/2}g$

Vemos que como en el caso de polea ideal el signo de la aceleración depende de la diferencia entre masas, pero que la presencia de la polea reduce su valor. Vemos también que el valor del radio de la polea es indiferente (aunque el hecho de que se trata de un cilindro permanece en el factor 1/2).

3 Tensiones

Una vez que conocemos la aceleración es inmediato hallar la tensión de la cuerda a cada lado.

$T_1 = m_1(g+a) = \frac{2m_1m_2+m_1M/2}{m_1+m_2+M/2}g\qquad\qquad T_2 = m_2(g-a) = \frac{2m_1m_2+m_2M/2}{m_1+m_2+M/2}g$

4 Fuerza en el soporte

La polea se ve sometida también a una fuerza externa en su soporte, ya que su centro de masas no se está acelerando, lo que nos dice que la fuerza neta sobre la polea es nula

$\vec{0}=\vec{F}_\mathrm{ext}+(-\vec{T}_1)+(-\vec{T}_2) \qquad\Rightarrow\qquad \vec{F}_\mathrm{ext}=\vec{T}_1+\vec{T}_2 = \frac{4m_1m_2+(m_1+m_2)M/2}{m_1+m_2+M/2}g\vec{k}$

Máquina de Atwood con polea pesada

De Laplace

Contenido

1 Enunciado

2 Aceleración

3 Tensiones

4 Fuerza en el soporte

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES