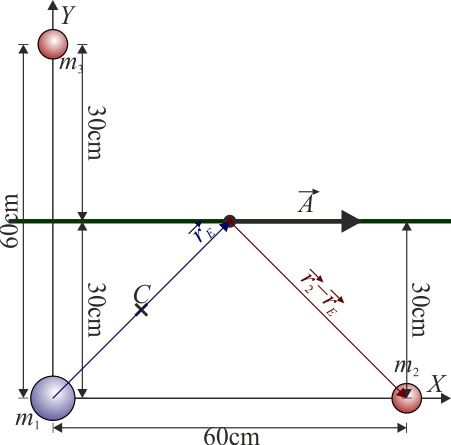
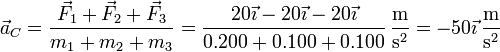Sólido formado por tres partículas

De Laplace

Contenido

1 Enunciado
2 Centro de masas
3 Momento de inercia
4 Aceleración del CM

1 Enunciado

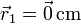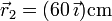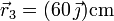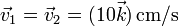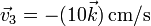Un sólido está formado por tres partículas, una de masa 200 g situada en $\vec{r}_1=\vec{0}\,\mathrm{cm}$ y dos de 100 g que se encuentran en $\vec{r}_2=(60\,\vec{\imath})\mathrm{cm}$ y $\vec{r}_3=(60\,\vec{\jmath})\mathrm{cm}$ , respectivamente. Las velocidades de las masas valen cada una $\vec{v}_1 = \vec{v}_2=(10\vec{k})\,\mathrm{cm}/\mathrm{s}$ y $\vec{v}_3=-(10\vec{k})\,\mathrm{cm}/\mathrm{s}$ .

¿Cuál es la posición del centro de masas del sistema?
¿Cuánto vale el momento de inercia de este sólido respecto a un eje que pasa por 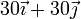$30\vec{\imath}+30\vec{\jmath}$ (cm) y tiene la dirección del vector $\vec{\imath}$ ?
Si en este sólido se aplica sobre la masa de 200 g una fuerza 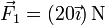$\vec{F}_1 = (20\vec{\imath})\,\mathrm{N}$ y sobre las masas de 100 g una fuerza $\vec{F}_2 =\vec{F}_3 = (-20\vec{\imath})\,\mathrm{N}$ . ¿Cuánto vale la aceleración del centro de masas del sólido?

2 Centro de masas

La posición del centro de masas es una media ponderada de las posiciones de las tres partículas

$\vec{r}_C = \frac{m_1\vec{r}_1+m_2\vec{r}_2+m_3\vec{r}_3}{m_1+m_2+m_3}=\frac{200(\vec{0})+100(60\vec{\imath})+100(60\vec{\jmath})}{200+100+100}\,\mathrm{cm}=\left(15\vec{\imath}+15\vec{\jmath}\right)\mathrm{cm}$

3 Momento de inercia

El momento de inercia de un sólido respecto a un eje es una suma de las masas multiplicadas por las distancias al eje elevadas al cuadrado

$I = m_1R_1^2+m_2R_2^2+m_3R_3^2\,$

En este caso, el eje es uno tangente al plano del triángulo que forman las masas y paralelo a uno de los lados pasando por el centro del otro. Las tres distancias a este eje son iguales entre sí y a

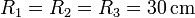
$R_1 = R_2=R_3 = 30\,\mathrm{cm}$

lo que nos da el momento de inercia

$I = (200\cdot 30^2 + 100\cdot 30^2+100\cdot 30^2)\mathrm{g}\cdot\mathrm{cm}^2 = 360\,000\,\mathrm{g}\cdot\mathrm{cm}^2=0.036\,\mathrm{kg}\cdot\mathrm{m}^2$

Caso de no verse geométricamente, las distancias pueden hallarse analíticamente mediante la fórmula

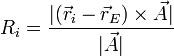
$R_i = \frac{|(\vec{r}_i-\vec{r}_E)\times\vec{A}|}{|\vec{A}|}$

siendo 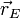$\vec{r}_E$ un punto del eje y $\vec{A}$ un vector director de éste. Así, por ejemplo, para la segunda masa tenemos que midiendo las distancias en centímetros

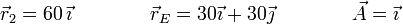
$\vec{r}_2 = 60\,\vec{\imath}\qquad\qquad \vec{r}_E = 30\vec{\imath}+30\vec{\jmath}\qquad\qquad \vec{A} = \vec{\imath}$

lo que da

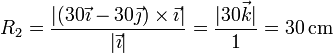
$R_2 = \frac{|(30\vec{\imath}-30\vec{\jmath})\times\vec{\imath}|}{|\vec{\imath}|} = \frac{|30\vec{k}|}{1} = 30\,\mathrm{cm}$

y de manera análoga para las otras dos masas.

4 Aceleración del CM

La aceleración del centro de masas de un sólido es igual a la resultante de las fuerzas aplicadas dividida por la masa total del sólido

$\vec{a}_C=\frac{\vec{F}_1+\vec{F}_2+\vec{F}_3}{m_1+m_2+m_3} = \frac{20\vec{\imath}-20\vec{\imath}-20\vec{\imath}}{0.200+0.100+0.100}\,\frac{\mathrm{m}}{\mathrm{s}^2} = -50\vec{\imath}\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Sólido formado por tres partículas

De Laplace

Contenido

1 Enunciado

2 Centro de masas

3 Momento de inercia

4 Aceleración del CM

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES