Vuelco de un camión

De Laplace

Contenido

1 Enunciado
2 Solución
3 Condición de vuelco
4 Condición de derrape
5 Análisis usando resultante y momento

1 Enunciado

Un camión de mudanzas va cargado de forma que su centro de gravedad se encuentra a 3.0 m del suelo. Si la distancia entre ruedas del camión es de 2.40 m, ¿cuál es la máxima velocidad con la que puede tomar una rotonda de 20 m de radio sin volcar? ¿Cuál es el valor mínimo que debe tener el coeficiente de rozamiento estático con el suelo para que el camión no derrape?

2 Solución

En este estudio se va a tratar el problema del vuelco en una situación dinámica, usando un modelo muy simplificado del problema. Una versión realista debería tener en cuenta efectos como la suspensión del camión, los sistemas de control de que dispone y el que un camión no es un único sólido rígido, sino un conjunto de ellos.

Modelaremos el camión como un bloque de anchura 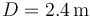$D = 2.4\,\mathrm{m}$ tal que su CM se encuentra situado en un punto intermedio entre las dos ruedas y a una altura 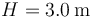$H = 3.0\,\mathrm{m}$ (la altura real del camión es irrelevante).

Cuando el camión toma una curva, adquiere una aceleración normal, radial y hacia adentro.

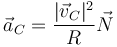
$\vec{a}_C = \frac{|\vec{v}_C|^2}{R}\vec{N}$

En esta expresión $R$ es el radio de giro del CM del camión. Suponemos que en los 20 m ya va incluida la mitad de la anchura del camión.

Según la segunda ley de Newton, debe haber una fuerza radial y hacia adentro causante de esta aceleración. Esta fuerza es la que ejerce el suelo de la carretera sobre las ruedas del camión (a su vez reacción de la que las ruedas ejercen sobre el suelo).

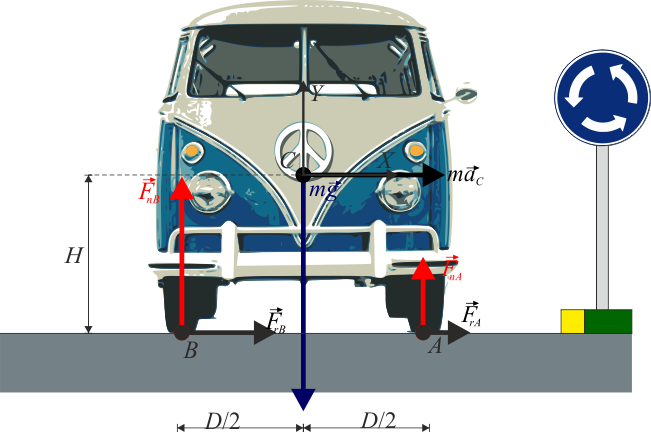
Considerando solo una sección del sólido, podemos describirlo como sometido a tres fuerzas:

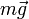
Su peso, $m\vec{g}$
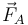
La fuerza de reacción sobre las ruedas interiores $\vec{F}_A$
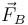
La fuerza de reacción sobre las ruedas exteriores $\vec{F}_B$

Las fuerzas sobre las ruedas se componen de una parte normal y hacia arriba, y de una tangente, radial y hacia adentro. Esta última es debida al rozamiento lateral. Puesto que este es usualmente muy intenso para un neumático, podemos suponer por ahora que la fuerza de rozamiento puede alcanzar el valor que sea necesario.

La ecuación para el movimiento del centro de masas nos da

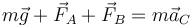
$m\vec{g}+\vec{F}_A+\vec{F}_B = m\vec{a}_C$

Suponiendo un sistema de ejes centrado en el punto de contacto de la rueda exterior con el suelo, con el eje Y en la vertical y el eje X radial y hacia adentro de la rotonda, esta ecuación vectorial se descompone en

$\left\{\begin{array}{rcl}F_{rA} + F_{rB} & = & \displaystyle m\frac{|\vec{v}_C|^2}{R} \\ && \\ F_{nA}+F_{nB}-mg & = & 0 \end{array}\right.$

A esta ecuación debemos añadir la ecuación para el momento de las fuerzas. Tomando el momento respecto al CM nos queda

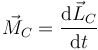
$\vec{M}_C = \frac{\mathrm{d}\vec{L}_C}{\mathrm{d}t}$

El último término representa el giro del camión alrededor de sí mismo. En este modelo sencillo podemos suponer que este término es despreciable y que el movimiento del camión es esencialmente uno de traslación. Según esto

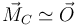
$\vec{M}_C \simeq \vec{O}$

Respecto a este punto, el momento del peso es nulo, por estar aplicado en el propio centro de masas. Para el resto de las fuerzas tenemos

$\vec{M}_C=\left(-\frac{D}{2}F_{nB}+HF_{rB}+HF_{rA}+\frac{D}{2}F_{nA}\right)\vec{k}$

Vemos que la reacción sobre la rueda exterior debe compensar el momento debido a las otras tres. se cumple

$F_{nB}-F_{nA}=\frac{2H}{D}\left(F_{rA}+F_{rB}\right)=\frac{2mH|\vec{v}_C|^2}{DR}$

Combinando esto con la ecuación para la fuerza normal

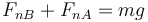
$F_{nB}+F_{nA}=mg\,$

obtenemos

$F_{nB}=\frac{mg}{2}+\frac{mH|\vec{v}|^2}{RD}\qquad\qquad F_{nA}=\frac{mg}{2}-\frac{mH|\vec{v}_C|^2}{RD}$

3 Condición de vuelco

El vínculo que ejerce el suelo sobre las ruedas es unilateral. Las ruedas están apoyadas en el suelo, pero no pegadas a él. Por ello, $F n A$ (y $F n B$ ) debe ser siempre positivo. Si en la ecuación anterior se hiciera negativo querría decir que el suelo no es capaz de retener al camión y éste vuelca.

Esto nos da la condición para la velocidad máxima

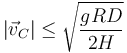
$|\vec{v}_C|\leq \sqrt{\frac{gRD}{2H}}$

El resultado nos informa de que cuanto mayor sea la altura del CM menor debe ser la rapidez máxima si no desea que vuelque (dicho de otra forma, que hay que bajar el CM para evitar el vuelco). Una mayor anchura de ejes, en cambio, estabiliza el camión. También aumenta la rapidez máxima si la rotonda tiene gran radio. El resultado es independiente de la masa del camión (esto se podía haber deducido por análisis dimensional).

Para los datos del enunciado, esta rapidez máxima es

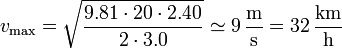
$v_\mathrm{max}=\sqrt{\frac{9.81\cdot 20\cdot 2.40}{2\cdot 3.0}}\simeq 9\,\frac{\mathrm{m}}{\mathrm{s}}= 32\,\frac{\mathrm{km}}{\mathrm{h}}$

El resultado es una rapidez muy reducida para lo habitual en el tráfico. En realidad, existe un margen mayor gracias a los sistemas de control de estabilidad de los vehículos. Hay que destacar que si la altura del CM se baja a 1m, esta velocidad límite supera los 55km/h.

Puesto que la reacción sobre las ruedas exteriores es mayor que sobre las interiores se produce un mayor desgaste en las exteriores. Este efecto es importante en un vehículo de carreras, ya que en un circuito la mayoría de las curvas son en uno de los sentidos.

Nótese también que carecemos de información suficiente para determinar cada una de las fuerzas de rozamiento; solo podemos determinar su suma. Esto es un ejemplo de problema indeterminado, en el que tenemos más incógnitas que ecuaciones.

4 Condición de derrape

En el análisis anterior se ha supuesto que las fuerzas de rozamiento con el suelo podían tener cualquier valor, por grande que fuera. Sin embargo, esto no es cierto. Existe un límite dado por el agarre de las ruedas, es decir por el coeficiente de rozamiento estático. Debe cumplirse que

$|F_{rA}| \leq \mu |F_{nA}|\qquad\qquad |F_{rB}| \leq \mu |F_{nB}|$

Sumando estos dos límites

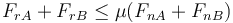
$F_{rA}+F_{rB} \leq \mu(F_{nA}+F_{nB})$

y por el teorema de la cantidad de movimiento, esto equivale a

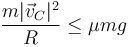
$\frac{m|\vec{v}_C|^2}{R}\leq \mu mg$

lo que nos da una nueva cota para la rapidez

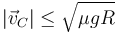
$|\vec{v}_C| \leq \sqrt{\mu g R}$

Esta condición nos dice que si la velocidad supera esta cota, las fuerzas de rozamiento no son capaces de producir la aceleración normal deseada. Esto implica una menor aceleración normal y un mayor radio de curvatura

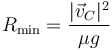
$R_\mathrm{min}=\frac{|\vec{v}_C|^2}{\mu g}$

El resultado es que el camión se sale de la curva prevista, desviándose hacia el exterior de la curva, patinando lateralmente sus ruedas. Esto es lo que se conoce como derrape.

La condición de vuelco y la de derrape no son incompatibles. Tenemos las cuatro posibilidades:

Si la velocidad es moderada y el centro de masas es bajo, ni vuelca ni derrapa.
Si la velocidad es alta y el centro de masas bajo, lo más probable es que derrape. Esto es lo que le ocurriría a un coche.
Si la velocidad es moderada, pero el centro de masas está muy alto, es más probable que vuelque. Esto es lo que le ocurriría a un camión muy cargado.
Si la velocidad es muy elevada y el centro de masas está muy alto, el vuelco iría acompañado de derrape.

5 Análisis usando resultante y momento

El estudio anterior se ha realizado considerando la fuerza de reacción (tangencial y normal) en cada uno de los dos puntos.

Una forma alternativa de estudiar este problema es considerar un sistema equivalente. Todo sistema de fuerzas se puede sustituir por una sola fuerza (la resultante de todas las aplicadas) y un momento respecto a un punto.

Cuando se tienen solo dos fuerzas aplicadas no hay gran ventaja entre usar éstas o emplear la resultante y el momento. Cuando son más de dos las fuerzas aplicadas, ya el uso de la resultante y el momento es ventajoso.

Veamos como sería.

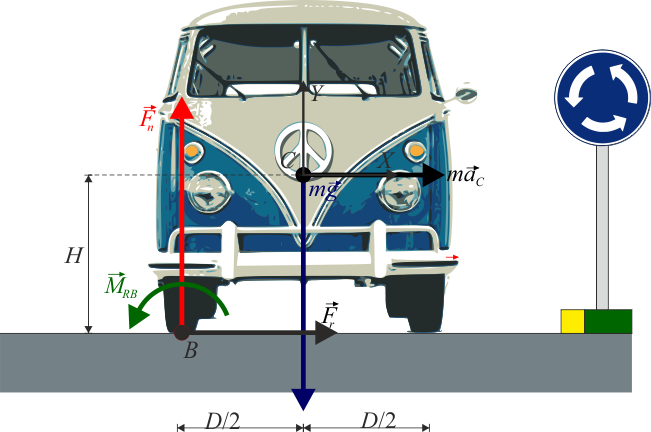
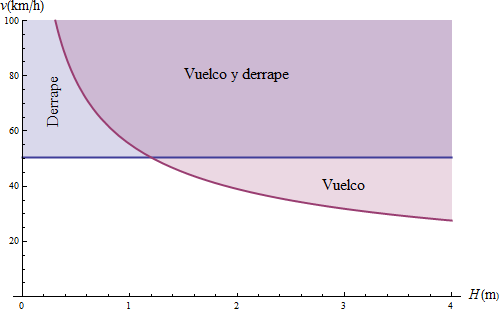
Sabemos que si vuelca lo hará apoyándose en el punto B, por lo que elegimos este punto como centro de reducción. Consideramos entonces que el conjunto de todas las fuerzas de reacción es equivalente a una fuerza aplicada en B

$\vec{F}_R = F_r\vec{\imath}+F_n\vec{\jmath}$

y a un momento alrededor de un eje que pasa por B

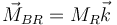
$\vec{M}_{BR}=M_R\vec{k}$

Nótese que no decimos que no haya fuerza aplicada en A, o que esta $\vec{F}_R$ sea la fuerza que realmente se ejerce en B. No, lo que hacemos es sustituir el verdadero sistema de dos fuerzas por uno equivalente.

La ecuación de movimiento para el CM del sólido queda entonces

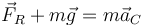
$\vec{F}_R+m\vec{g}=m\vec{a}_C$

que desarrollada en componentes da

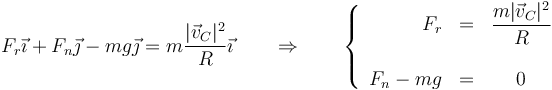
$F_r\vec{\imath}+F_n\vec{\jmath}-mg\vec{\jmath}=m\frac{|\vec{v}_C|^2}{R}\vec{\imath}\qquad\Rightarrow\qquad \left\{\begin{array}{rlc} F_r & = & \displaystyle \frac{m|\vec{v}_C|^2}{R}\\ && \\ F_n - mg & = & 0 \end{array}\right.$

A la hora de aplicar la ecuación para los momentos hay que tener cuidado. Estamos considerando la condición de vuelco inminente, es decir que el camión está a punto de volcar, pero aun no se le aplica fuerza suficiente para hacerlo. En ese caso, se anula el momento de las fuerzas respecto al CM

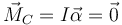
$\vec{M}_C = I\vec{\alpha}=\vec{0}$

Esta anulación vale respecto al CM o respecto a un punto fijo, pero no respecto a un punto acelerado como B. Para este tenemos que

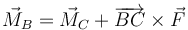
$\vec{M}_B = \vec{M}_C+\overrightarrow{BC}\times \vec{F}$

El primer miembro de esta ecuación es igual a

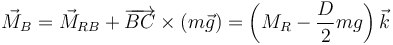
$\vec{M}_B= \vec{M}_{RB}+\overrightarrow{BC}\times(m\vec{g}) = \left(M_R - \frac{D}{2}mg\right)\vec{k}$

La fuerza de reacción en B no tiene momento por estar aplicada en el propio punto (o dicho de otra forma, el momento de todas las fuerzas de reacción ya está incluido en 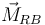$\vec{M}_{RB}$ ).

El segundo miembro vale

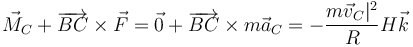
$\vec{M}_C+\overrightarrow{BC}\times \vec{F}=\vec{0}+\overrightarrow{BC}\times m\vec{a}_C = -\frac{m\vec{v}_C|^2}{R}H\vec{k}$

Igualando nos queda la ecuación

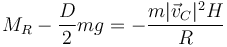
$M_R - \frac{D}{2}mg = -\frac{m|\vec{v}_C|^2H}{R}$

Tenemos entonces ya toda la información para hallar la fuerza y el momento de reacción

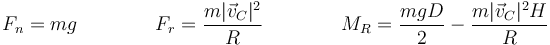
$F_n = mg \qquad\qquad F_r = \frac{m|\vec{v}_C|^2}{R}\qquad\qquad M_R = \frac{mgD}{2}-\frac{m|\vec{v}_C|^2H}{R}$

Condición de vuelco: Las fuerzas de reacción pueden impedir que el camión gire alrededor de B hundiéndose en el suelo (lo que sería un giro en sentido horario), pero no que el camión vuelque, separándose del suelo. Por tanto, el momento de las fuerzas de reacción va en sentido antihorario, es decir, es positivo

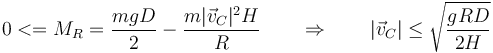
$0 <= M_R = \frac{mgD}{2}-\frac{m|\vec{v}_C|^2H}{R}\qquad\Rightarrow\qquad |\vec{v}_C|\leq \sqrt{\frac{gRD}{2H}}$

Condición de derrape: La fuerza de rozamiento no puede superar el límite del rozamiento estático, por lo que

$F_r\leq \mu F_n\qquad\Rightarrow\qquad |\vec{v}_C| \leq \sqrt{\mu g R}$

Vemos que, como cabía esperar, las condiciones son las mismas que las obtenidas por el otro método.

Vuelco de un camión

De Laplace

Contenido

1 Enunciado

2 Solución

3 Condición de vuelco

4 Condición de derrape

5 Análisis usando resultante y momento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES