Equilibrio de una barra apoyada
De Laplace
Contenido |
1 Enunciado
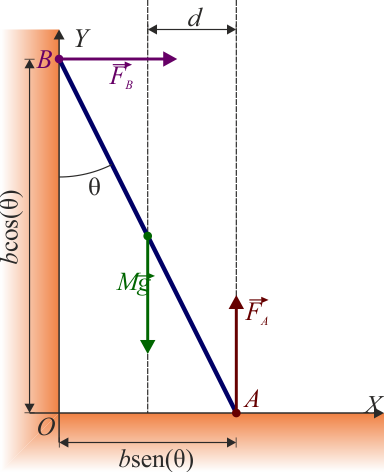
Supongamos que tenemos una barra de masa M y longitud b apoyada en el suelo y en una pared vertical.
- Suponga primero que no hay rozamiento con las superficies y que la barra forma un ángulo θ con la vertical. ¿Puede quedarse en equilibrio la barra para algún valor de θ?
- Suponga ahora que la barra posee un coeficiente de rozamiento estático μ con el suelo. ¿Para qué ángulos puede alcanzarse entonces el equilibrio?
2 Sin rozamiento
La condición para que un sólido esté en equilibrio es que la fuerza resultante y el momento resultante (respecto de cualquier punto) sean nulos.

En este sistema tenemos tres fuerzas actuando sobre la barra
- Su peso,
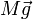
- La reacción del suelo, aplicada en el punto A,
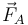
- La reacción de la pared, aplicada en el punto B,
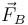
En principio, el peso de la barra no es una sola fuerza, sino una infinitud de ellas (cada trocito de barra tiene su propio peso). Lo que ocurre es que este sistema de infinitas fuerzas diferenciales es equivalente a una sola fuerza de valor el peso total y aplicada en el centro de gravedad del sólido.
Si situamos el origen de coordenadas en la esquina, el valor del peso y su punto de aplicación son
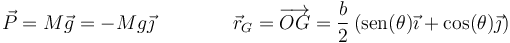
La reacción del suelo se aplica en el punto A de contacto de la barra con él. Por ser una superficie sin rozamiento, su dirección es puramente normal al suelo. Por ser un vínculo unilateral, su sentido es necesariamente hacia afuera del suelo
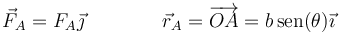
La reacción de la pared se aplica en el punto de apoyo en ella, B, su dirección es también perpendicular y su sentido es hacia afuera

La condición de equilibrio es, en primer lugar, que la suma de fuerzas sea igual a cero
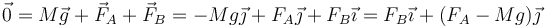
lo cual implica, separando por componentes,

es decir, la reacción del suelo debe compensar al peso, mientras que la de la pared no tiene que compensar a nadie, por lo que es nula.
No basta con que la resultante sea nula, también debe serlo el momento resultante. Para que se anule el momento, podemos tomar cualquier punto como referencia. Considerando el momento respecto al punto O, la esquina de la pared con el suelo, debe ser
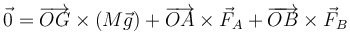
Del equilibrio de fuerzas, ya establecimos que la fuerza ejercida por la pared es nula, mientras que la ejercida por el suelo es opuesta al peso. Esto quiere decir que este sistema de fuerzas es equivalente a un par formado por el peso y la reacción del suelo. El brazo de este par no es nulo, ya que la recta de acción del peso no es la misma que la de la reacción del suelo. El brazo del par vale
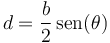
Por lo que el módulo del momento vale, para cualquier punto,
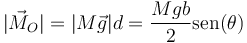
Solo para el caso θ = 0, es decir, para una barra completamente vertical, es posible conseguir un equilibrio (y en ese caso, será inestable, pues se trata de un péndulo invertido). Por lo tanto, no existe ningún ángulo, aparte del trivial, para el cual se pueda conseguir el equilibrio si no hay rozamiento. Para conseguir que una escalera se quede quieta al apoyarla en una pared es necesario calzarla.
3 Con rozamiento
Cuando existe rozamiento entre el suelo y la barra, ya la fuerza de reacción del suelo no es puramente normal, sino que posee una componente tangente a la superficie y que se opone al posible movimiento
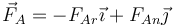
cumpliéndose, en una situación de equilibrio estático
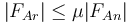
La reacción de la pared sigue siendo puramente normal, aunque ya no tiene por qué ser nula. Llevando esto a la ecuación de equilibrio de fuerzas queda

lo que nos da las ecuaciones escalares

Los valores de las componentes horizontales aun no están determinados, aunque sí sabemos que deben cumplir
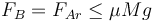
Aplicando ahora la anulación de los momentos respecto al punto O obtenemos
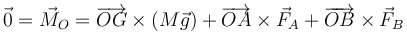
Sustituyendo cada fuerza y cada posición respecto al punto O de la esquina
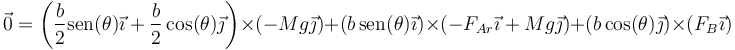
Esta expresión se simplifica mucho porque varios productos vectoriales se anulan y queda finalmente la ecuación
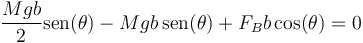
Alternativamente, es más simple si elegimos un centro de reducción adecuado. En este caso, tomamos el punto de apoyo A, conseguimos que se anule el momento de la fuerza de rozamiento y el de la normal en ese punto y la condición de equilibrio se reduce a
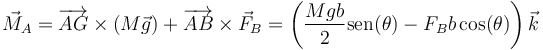
De cualquiera de las dos formas obtenemos el valor de FB
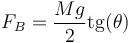
y, por ser iguales, el de la fuerza de rozamiento
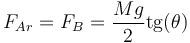
La condición para que sea posible el equilibrio es que esta fuerza de rozamiento sea menor que su valor límite
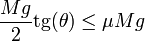
lo que nos da la condición para el ángulo θ
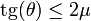
Por tanto, es posible el equilibrio para un rango de ángulos que será mayor cuanto mayor sea el coeficiente de rozamiento con el suelo.
Otra forma de ver esta solución es considerar que la barra está sometida a dos pares de fuerzas:
- El formado por el peso y la componente normal de la reacción del suelo, calculado en el primer apartado, cuyo momento es
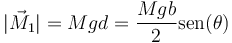
- El formado por la reacción de la pared y la fuerza de rozamiento, cuyo brazo mide bcos(θ) y cuyo par es
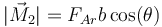
Uno de los pares intenta girar la barra hacia un lado y el otro en el sentido opuesto. El equilibrio se dará cuando ambos pares se anulen mutuamente, esto es, si
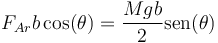
lo cual nos da de nuevo la condición que ya conocemos
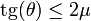
Gráficamente puede demostrarse que para que se produzca el equilibrio en un sólido sometido a tres fuerzas debe existir algún punto (en la figura, el punto P) en el que se corten las tres rectas de acción de las fuerzas (y que además estas se anulen entre sí). Puesto que la fuerza de rozamiento no puede superar un cierto valor, esto limita el rango de valores posibles de la fuerza de reacción en el suelo y define cuándo existe este punto y cuando no.