Problemas de electrostática en presencia de conductores

De Laplace

Contenido 1 Capacidad de una esfera 2 Conductores esféricos concéntricos 3 Conductores cilíndricos coaxiales 4 Campo entre dos placas planas y paralelas 5 Dos placas conductoras y una densidad de carga intermedia 6 Una esfera conductora rellena de una densidad de carga 7 Esfera conductora con dos huecos esféricos 8 Sistema de cuatro conductores prismáticos 9 Sistema simétrico de cuatro conductores 10 Cuatro planos conductores paralelos 11 Dos planos y tres superficies esféricas 12 Distribución de carga dentro de esferas conductoras 13 Dos hemisferios y una corteza esférica 14 Dos cargas en sendos lados de un plano conductor 15 Una nube frente al plano de tierra 16 Carga puntual frente a una esfera conductora con potencial fijado 17 Carga puntual frente a una esfera conductora con carga fijada 18 Carga en un hueco conductor esférico 19 Bloque entre dos placas conductoras 20 Cubo entre cuatro placas conductoras 21 Prisma entre placas conductoras 22 Fuerza sobre una partícula semiesférica

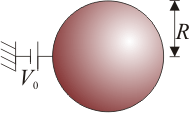
1 Capacidad de una esfera

Una esfera metálica de radio a se encuentra a potencial V₀ respecto al infinito. No hay más conductores en el sistema. Determine el potencial y el campo eléctrico en todos los puntos del espacio, así como la carga almacenada en la esfera conductora.

Solución

2 Conductores esféricos concéntricos

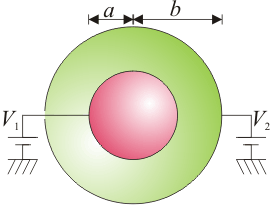
Se tiene un sistema de dos conductores. Uno de ellos es una esfera metálica maciza de radio a. El otro es una fina corteza esférica metálica, de radio b, concéntrica con la anterior. Calcule el potencial en todos los puntos del espacio en los casos siguientes.

1. La esfera interior se encuentra a potencial V₁ y la exterior a potencial V₂.
2. La esfera interior almacena una carga Q₁ y la exterior una carga Q₂.
3. La esfera interior almacenada una carga Q₁ y la exterior se encuentra a un potencial V₂.
4. Calcule asimismo la energía almacenada en el sistema de dos esferas, para las tres situaciones indicadas.

3 Conductores cilíndricos coaxiales

Un cilindro macizo de gran longitud h y radio a se encuentra rodeado de una corteza cilíndrica concéntrica, la misma longitud L, radio interior b y exterior c, también metálica.

La corteza exterior se encuentra permanentemente a tierra.

Determine la distribución de potencial y de campo eléctrico entre los dos cilindros cuando el cilindro interior se encuentra a potencial V₁. Calcule la carga almacenada en el cilindro interior.

Desprecie los efectos de borde.

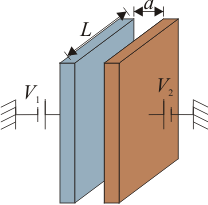
4 Campo entre dos placas planas y paralelas

Dos placas conductoras cuadradas de lado L se sitúan paralelamente a una distancia a la una de la otra (). Los

potenciales de ambas placas son V₁ y V₂, respectivamente. Calcule el valor aproximado de

1. El potencial en los puntos entre ambas placas.
2. El campo eléctrico en el espacio intermedio.
3. La carga almacenada en la caras de las placas enfrentadas a la otra placa.

Desprecie los efectos de borde.

5 Dos placas conductoras y una densidad de carga intermedia

Dos placas metálicas, planas y paralelas, de sección S, se encuentran situadas a una distancia a la una de la otra. La placa inferior se pone a una tensión V₁, mientras que la superior se encuentra a tensión V₂. El espacio entre las placas está ocupado por una capa de un material cargado con una densidad uniforme ρ₀.

1. Determine el potencial y el campo eléctrico en todos los puntos entre las placas.
2. Calcule la energía eléctrica almacenada en el sistema.
3. Halle la fuerza sobre las placas y sobre el material intermedio.

Solución

6 Una esfera conductora rellena de una densidad de carga

Una superficie esférica conductora de radio R, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma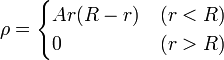

1. Calcule el campo eléctrico en todos los puntos del espacio.
2. Calcule el valor de la carga almacenada en la esfera conductora.
3. Halle el potencial eléctrico en el centro de la esfera.
   1. A partir del campo eléctrico.
   2. Por integración directa a partir de las densidades de carga.
4. Halle la energía electrostática almacenada en el sistema.

Solución

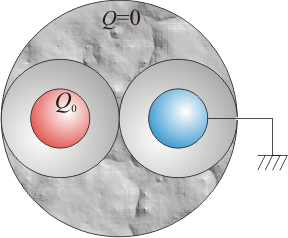
7 Esfera conductora con dos huecos esféricos

En una esfera metálica de radio R se han hecho dos cavidades, también esféricas, de radio R / 2. Concéntricas con cada una de estos huecos se hallan sendas esferas metálicas de radio R / 4. No hay más conductores en el sistema. Suponga que la esfera exterior se encuentra aislada y descargada; una de las esferas interiores almacena una carga Q₀ y la otra se encuentra a tierra. ¿Cuál es la carga en cada conductor? ¿Y el potencial?

Halle la energía almacenada en el sistema.

8 Sistema de cuatro conductores prismáticos

Se tiene un sistema de cuatro conductores tal como se indica en la figura. Uno de ellos (conductor “4”) es un prisma cuadrado hueco de lado 43 mm y longitud 50 mm. Este conductor se encuentra siempre a tierra.

En su interior se encuentran tres conductores. El conductor “1” es un paralelepípedo de lados 41 mm, 20 mm y 50 mm. Los conductores “2” y “3” son sendos prismas cuadrados de lado 20 mm y altura 50 mm. la distancia entre superficies conductoras vecinas es de 1 mm.

1. Teniendo en cuenta la pequeñez relativa de las diferentes distancias calcule, aproximadamente, las cargas que almacenan los conductores 1, 2 y 3, cuando sus tensiones son 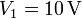, 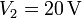y .
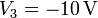2. Para la configuración anterior, calcule la energía electrostática almacenada en el sistema.
3. Si el conductor 1 se encuentra a tensión 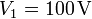, el 2 aislado y descargado y el 3 a tierra, ¿cuáles son las cargas y los potenciales de los tres conductores? ¿Y la energía electrostática almacenada en el sistema?

9 Sistema simétrico de cuatro conductores

Considere el sistema de cuatro conductores de la figura. Está formado por cuatro superficies esféricas situadas dos dentro de las otras dos (no concéntricamente). En este sistema, los conductores 1 y el 2 son simétricos con el 4 y el 3, respectivamente.

Para este sistema, ¿qué coeficientes de capacidad e inducción son nulos? ¿Cuáles positivos? ¿Cuáles negativos? ¿Cuáles iguales entre sí? ¿Qué

Suponga que mediante finos hilos conductores se conecta el conductor 1 con el 3, y el 2 con el 4 (estos cables atraviesan, sin hacer contacto, los conductores 2 y 3). ¿Cómo queda la nueva matriz de capacidades a partir de la matriz del sistema original?

10 Cuatro planos conductores paralelos

Se tiene un sistema formado por cuatro placas conductoras, todas ellas cuadradas y de lado L, situadas paralelamente. Las distancias entre placas consecutivas son, respectivamente, a, 3a y 2a ().

Las placas exteriores se encuentran a tierra en todo instante.

1. Inicialmente la segunda placa almacena una carga Q, mientras que la tercera está aislada y descargada. determine el potencial al que se encuentra cada placa, así como la carga que almacena cada una.
2. Para el caso anterior, determine el campo eléctrico en todos los puntos entre las placas.
3. Si ahora se conectan las dos placas intermedias, ¿cómo cambian las cargas y los potenciales de las distintas placas? ¿Y los campos eléctricos entre las placas?
4. Determine la variación de energía entre el estado anterior y el posterior a la conexión.

Solución

11 Dos planos y tres superficies esféricas

Dos discos conductores de radio 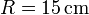, paralelos y separados una distancia 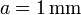están conectados a sendas esferas conductoras, también de radio R, mediante unos hilos conductores muy largos. Una de las esferas está completamente rodeada por una carcasa conductora esférica, conectada a tierra, de radio 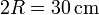, espesor despreciable, y concéntrica con la esfera. El sistema de conductores se encuentra en el vacío.

1. Determine la matriz de coeficientes de capacidad del sistema en función de sus parámetros geométricos. Justifique las aproximaciones que haga.
2. Estando el sistema inicialmente descargado, se conecta la esfera sin carcasa a una fuente de potencial fijo 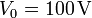. Determine la carga eléctrica en cada una de las superficies conductoras (esferas, discos y carcasa esférica) cuando el sistema ha alcanzado el equilibrio electrostático.
3. Para la situación anterior, determine la energía almacenada en el sistema.

12 Distribución de carga dentro de esferas conductoras

Una esfera de radio R posee una carga Q₁ distribuida en su volumen de modo que la densidad volumétrica es ρ(r) = Ar. A su alrededor se disponen dos superficies esféricas metálicas concéntricas, de radios 2R y 4R, respectivamente. Estas esferas están aisladas y descargadas.

1. Calcule la constante A en función de la carga de la esfera y de su radio.
2. Calcule el campo eléctrico en todo el espacio y el potencial al que se encuentran las esferas conductoras.
3. Se conectan las dos esferas conductoras entre sí. ¿Cuál es el nuevo potencial y la nueva carga de cada esfera?

Solución

13 Dos hemisferios y una corteza esférica

Suponga el sistema de la figura, formada por una corteza esférica (conductor “1”) de radio interior b y exterior c. En su interior hay dos conductores prácticamente semiesféricos (“2” y “3”), de radio a y separados una pequeña distancia w. Despreciando los efectos de borde,

Halle los coeficientes de capacidad e inducción del sistema.

14 Dos cargas en sendos lados de un plano conductor

Dos cargas, + q y − q, se sitúan en los puntos 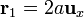y 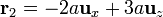, respectivamente.

1. Calcule la fuerza que experimenta cada carga y el trabajo necesario para traerlas desde el infinito hasta su posición final.
2. Suponga que se introduce un plano conductor, puesto a tierra, en x = 0. Halle la nueva fuerza que experimenta cada carga, así como la que sufre el plano conductor.
3. Calcule el trabajo necesario para introducir el plano.

15 Una nube frente al plano de tierra

Una nube de tormenta puede modelarse como un conjunto de dos cargas puntuales, 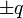, estando la carga positiva en su parte superior y la negativa en la inferior. La altura media de la nube es h₀ y el espesor de la nube Δh. Puede suponerse que .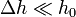

Para medir el momento dipolar de la nube, se coloca una carga q₁ sujeta a un dinamómetro en un punto sobre el plano de tierra (la carga puede suponerse en $z=0^+$), situado a una distancia x de la vertical de la nube.

1. Halle la fuerza que se mide, para una distancia x dada.
2. La nube, en su movimiento, modifica la distancia del observador a la vertical de la nube. Describa como varía la fuerza con x y halle para que valor de x es máxima la fuerza, así como este valor máximo.
3. Si 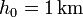, , 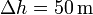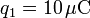y la fuerza máxima medida es de 0.2mN, calcule la carga almacenada en cada extremo de la nube.

16 Carga puntual frente a una esfera conductora con potencial fijado

Sea una superficie esférica, de radio R, de material conductor, puesta a potencial V₀, conocido, frente a la cual se encuentra una carga puntual q, situada en el punto (siendo 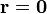el centro de la esfera).

1. Determine el potencial en todos los puntos del espacio, interiores y exteriores a la esfera.
2. Halle la fuerza que sufre la carga puntual.

17 Carga puntual frente a una esfera conductora con carga fijada

¿Cómo cambian los resultados del problema de una carga frente a una esfera si en lugar de estar fijado el potencial de la esfera, se sabe que ésta está aislada y almacena una carga Q?

¿Cuánto vale la fuerza sobre la carga q si la esfera está descargada?

¿Cómo varía con la distancia la fuerza que la esfera ejerce sobre la carga si Q es del mismo signo que q?

18 Carga en un hueco conductor esférico

¿Cómo cambian los resultados de los dos problemas de una carga frente a una superficie esférica, con potencial fijado y con carga fijada, si la carga puntual se encuentra en el interior de un hueco esférico?

19 Bloque entre dos placas conductoras

Dos placas conductoras planas y paralelas cuadradas, de lado L, se encuentran separadas una distancia 2b (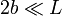). Entre ellas, y equidistante de ambas se encuentra un prisma conductor de anchura 2a, también de sección cuadrada de lado L.

El bloque posee una carga total Q₀. Entre las placas se establece una diferencia de potencial V₀

1. Calcule la carga en cada uno de los condensadores que forma el bloque con las placas.
2. Halle la energía almacenada en el sistema.
3. Calcule el valor del campo en cada uno de los espacios intermedios entre bloque y placas.
4. Halle la presión electrostática sobre las caras del bloque, así como la fuerza total sobre éste.
5. Calcule los valores numéricos de los resultados anteriores para , , , , .

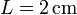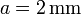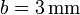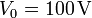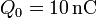20 Cubo entre cuatro placas conductoras

Cuatro placas cuadradas de lado 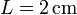, conductoras, se encuentran en la disposición cuadrada indicada en la figura.

Entre las cuatro placas, centrado, se encuentra un cubo conductor, de arista 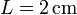, situado a una distancia 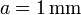de cada placa. El cubo está descargado en todo momento.

Si las cuatro placas se conectan a sendos generadores que fijan tensiones , , ,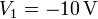

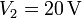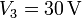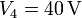
1. Halle la carga almacenada en cada una de las placas cuadradas.
2. Calcule la energía electrostática del sistema.
3. Calcule el valor del campo en cada uno de los condensadores que se forman.
4. Halle la presión electrostática en cada cara del cubo enfrentada a una placa, así como la fuerza electrostática total sobre el cubo.

Despréciense los efectos de borde y los debidos a las caras del cubo no enfrentadas a una placa.

Solución

21 Prisma entre placas conductoras

Se tiene el sistema de la figura, formado por un prisma triangular (“4”), cuya base es un triángulo equilátero de lado L, y cuya altura es también L. Este prisma está conectado a tierra. Frente a él se encuentran tres placas cuadradas de lado L situadas a distancia a, 2a y 3a (), respectivamente. Las placas “1” y “3” se conectan a un voltaje V₀, mientras que la “2” almacena una carga Q₀

1. Halle la matriz de coeficientes de capacidad en este sistema de cuatro conductores. Desprecie los efectos de borde.
2. Calcule la carga y el potencial de cada placa, así como la energía total del sistema.
3. Calcule la presión electrostática en cada cara del prisma. A partir de la presión, halle la fuerza neta sobre el prisma.

22 Fuerza sobre una partícula semiesférica

Se trata de hallar el campo eléctrico necesario para elevar en el aire una partícula metálica que reposa sobre un plano a tierra. La partícula conductora la podemos modelar como un hemisferio de radio a. Existe un campo eléctrico impuesto que, en puntos alejados de la semiesfera, es uniforme y perpendicular al plano conductor, .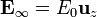

El potencial en todos los puntos por encima del plano y la partícula es de la forma

        

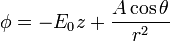
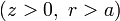
siendo r la distancia al centro de la semiesfera.

1. Determine el valor de A que hace que se satisfagan todas las ecuaciones y condiciones de contorno.
2. Halle la densidad de carga en la superficie de la semiesfera.
3. Calcule la presión electrostática en la superficie de la partícula. A partir de esta presión, halle la fuerza eléctrica sobre la partícula, empleando la relación .
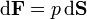4. Si la partícula es de aluminio y su radio vale 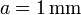, ¿qué campo es preciso para levantar esta partícula?