Problemas de Cinemática del punto (G.I.A.)
De Laplace
Contenido |
1 Ecuaciones de curvas
Expresa en forma parámetrica e implícita las siguientes curvas
- El eje OY
- Una circunferencia de radio a, contenida en el plano XY y con centro en el origen.
- Una parábola contenida en el plano YZ y con ecuación z = y2.
2 Trayectoria de una partícula
La trayectoria de una partícula viene dada por la ley horaria
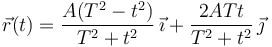
Determina la velocidad y aceleración de la partícula, los vectores del triedro intrínseco, así como la ecuación de la trayectoria. Calcula también las componentes intrínsecas de la velocidad y la aceleración ¿Cual es la expresión de un desplazamiento elemental 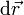 ? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula.
? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula.
3 Tiro oblicuo
Determina el movimiento de un proyectil disparado con una velocidad inicial v0 y un ángulo α con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria.
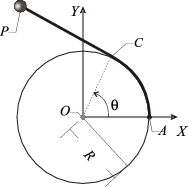
4 Cuerda enrollándose
Una partícula se mueve en el plano OXY mientras permanece
conectada a uno de los extremos de un hilo inextensible de longitud
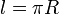 . El otro extremo está unido a un punto fijo A de una
circunferencia de radio R y centro O, cuyas coordenadas en el
sistema cartesiano OXY son
. El otro extremo está unido a un punto fijo A de una
circunferencia de radio R y centro O, cuyas coordenadas en el
sistema cartesiano OXY son 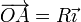 . Partiendo
de la posición inicial
. Partiendo
de la posición inicial 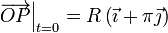 , el movimiento de la partícula con velocidad de módulo
constante v0 da lugar a que el hilo, que permanece siempre tenso,
se enrolle en dicha circunferencia. Utilizando como parámetro el
ángulo θ correspondiente al punto C donde desaparece el
contacto hilo--circunferencia, calcula:
, el movimiento de la partícula con velocidad de módulo
constante v0 da lugar a que el hilo, que permanece siempre tenso,
se enrolle en dicha circunferencia. Utilizando como parámetro el
ángulo θ correspondiente al punto C donde desaparece el
contacto hilo--circunferencia, calcula:
- Las ecuaciones paramétricas de la trayectoria seguida por la partícula.
- La ley horaria del movimiento θ = θ(t) y tiempo que tarda el hilo en enrollarse completamente sobre la circunferencia.
- La aceleración de la partícula.
- El triedro intrínseco de la trayectoria seguida por la partícula
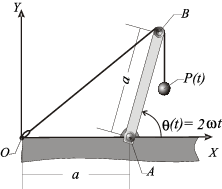
5 Barra girando en un plano
Una barra rígida AB de longitud 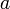 se mueve en un plano
vertical OXY, manteniendo su extremo A articulado en un punto
del eje horizontal de coordenadas
se mueve en un plano
vertical OXY, manteniendo su extremo A articulado en un punto
del eje horizontal de coordenadas 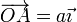 , y
verificando la ley horaria θ(t) = 2ωt, con
, y
verificando la ley horaria θ(t) = 2ωt, con 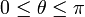 y siendo ω = cte. Un hilo inextensible de
longitud 2a tiene uno de sus extremos conectado al origen del
sistema de referencia (punto O), mientras que del otro cuelga
una partícula P que mantiene al hilo siempre tenso. El hilo se
apoya sobre una pequeña polea de radio despreciable situada en el
extremo B de la barra, de forma que el tramo
y siendo ω = cte. Un hilo inextensible de
longitud 2a tiene uno de sus extremos conectado al origen del
sistema de referencia (punto O), mientras que del otro cuelga
una partícula P que mantiene al hilo siempre tenso. El hilo se
apoya sobre una pequeña polea de radio despreciable situada en el
extremo B de la barra, de forma que el tramo 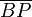 permanece siempre paralelo al eje OY (ver figura). Se pide:
permanece siempre paralelo al eje OY (ver figura). Se pide:
- Ecuaciones horarias del punto
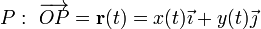 .
.
- Instante del tiempo tM en que la partícula alcanza su altura máxima.
- Radio de curvatura de la trayectoria seguida por P, en el instante considerado en el apartado anterior.
6 Velocidad de un punto en la superficie de la Tierra
La Tierra rota uniformemente con respecto a su eje con velocidad angular ω constante. Encuentra en función de
la latitud λ, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: 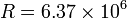 m.)
m.)
7 Punto moviéndose sobre una parábola
Un punto inicialmente en reposo en la posición x = a, y = b,
describe la parábola 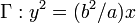 . Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
. Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
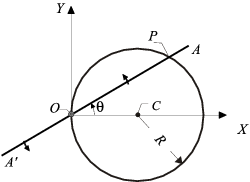
8 Barra deslizando sobre una circunferencia
En un plano OXY, se define el sistema cinemático formado por los dos siguientes elementos geométricos:
- una circunferencia fija, de radio R y centrada en el punto C de coordenadas
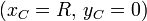 ;
;
- un segmento rectilíneo móvil A'A, de longitud superior a 4R, el cual gira con velocidad angular constante ω (en sentido antihorario) alrededor de un eje fijo que pasa por su punto medio O y es normal al plano OXY (eje OZ).
Sabiendo que el ángulo θ ( que forman OA y OX) es nulo en el instante inicial (t = 0); y considerando como móvil problema el punto P en el que se cortan el segmento A'A y la circunferencia , se pide:
- item Determinar las ecuaciones horarias,
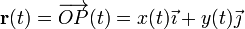 , del punto P, así como sus vectores velocidad,
, del punto P, así como sus vectores velocidad, 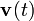 , y aceleración,
, y aceleración, 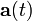 .
.
- Calcular las aceleraciones tangencial y normal de dicho punto P.
9 Parámetro arco de una hélice
Sea la hélice Γ descrita en un sistema de referencia cartesiano OXYZ por las siguientes ecuaciones paramétricas:
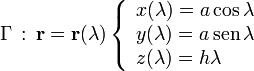
donde a y h son constantes conocidas.
- Determina la longitud recorrida sobre la hélice (parámetro arco) en función del parámetro λ
- Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
- Calcula su radio de curvatura.