Problemas de Inducción electromagnética
De Laplace
| Línea 21: | Línea 21: | ||
# Calcule la corriente que circula por el sistema en cada instante. Desprecie el efecto de la autoinducción. | # Calcule la corriente que circula por el sistema en cada instante. Desprecie el efecto de la autoinducción. | ||
| - | # Halle la fuerza que se ejerce sobre el conductor móvil | + | # Halle la fuerza que se ejerce sobre el conductor móvil |
| - | + | ||
| - | + | ||
===[[Barra deslizante sobre raíles]]=== | ===[[Barra deslizante sobre raíles]]=== | ||
Revisión de 09:57 19 may 2009
1 Barra que se mueve en un campo uniforme
Una barra metálica de longitud se mueve en el interior de un campo magnético uniforme
se mueve en el interior de un campo magnético uniforme  (
(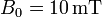 ) con velocidad constante
) con velocidad constante  , siendo
, siendo  perpendicular tanto al eje de la varilla como al campo magnético y de módulo
perpendicular tanto al eje de la varilla como al campo magnético y de módulo 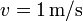 .
.
- Calcule la fuerza magnética sobre una carga
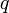 de la varilla. ¿Hacia donde se mueven las cargas positivas y negativas de la varilla?
de la varilla. ¿Hacia donde se mueven las cargas positivas y negativas de la varilla?
- La separación de carga alcanza el equilibrio cuando la fuerza eléctrica debido a dicha separación compensa exactamente la fuerza magnética. Usando esto, halle el campo eléctrico en el interior de la varilla.
- Calcule el voltaje entre los extremos de la varilla.
- Calcule la f.e.m. inducida, de acuerdo con la ley de Faraday, a lo largo de una curva formada por la varilla y un cierre por el exterior del campo magnético. Compruebe que coincide con el voltaje calculado en el apartado anterior.
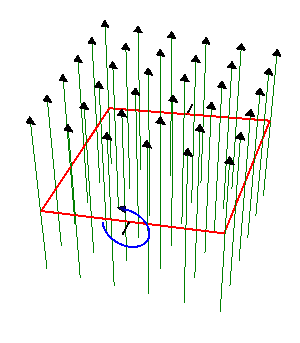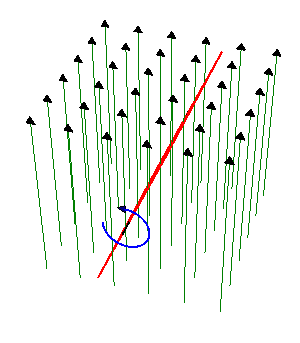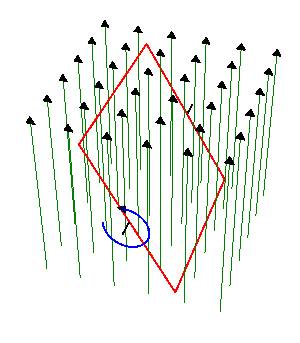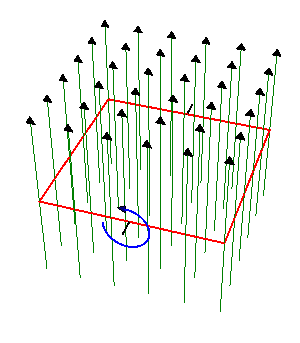
2 Espira cuadrada rotante en un campo B
Una espira cuadrada de lado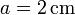 , de hilo de cobre de sección
, de hilo de cobre de sección 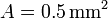 gira con frecuencia
gira con frecuencia 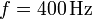 en el interior de un campo magnético uniforme de módulo
en el interior de un campo magnético uniforme de módulo 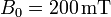 . El eje de giro es perpendicular al campo magnético.
. El eje de giro es perpendicular al campo magnético.
- Determine la corriente que se induce en la espira.
- Calcule la potencia instantánea disipada en la espira y la energía total disipada en un periodo de giro.
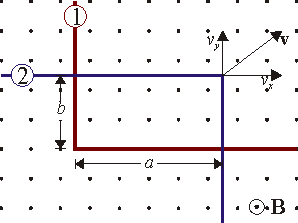
3 Conductor que se desplaza sobre otro
Se construye un sistema con dos hilos metálicos doblados en forma de L. Ambos hilos son de un material de conductividad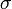 y sección
y sección  . Uno de los conductores ("1") es fijo, mientras que el segundo ("2") puede deslizarse manteniendo el contacto con el primero y su orientación, de forma que entre ambos conductores definen un rectángulo de base
. Uno de los conductores ("1") es fijo, mientras que el segundo ("2") puede deslizarse manteniendo el contacto con el primero y su orientación, de forma que entre ambos conductores definen un rectángulo de base  y altura
y altura 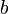 , siendo x = 0, y = 0 la esquina del conductor fijo. El conductor móvil se desplaza con velocidad constante, de forma que
, siendo x = 0, y = 0 la esquina del conductor fijo. El conductor móvil se desplaza con velocidad constante, de forma que

Todo el sistema está sometido a un campo magnético no uniforme 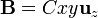 , perpendicular al plano de los conductores.
, perpendicular al plano de los conductores.
- Calcule la corriente que circula por el sistema en cada instante. Desprecie el efecto de la autoinducción.
- Halle la fuerza que se ejerce sobre el conductor móvil
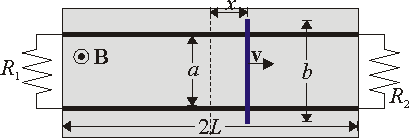
4 Barra deslizante sobre raíles
Se tienen dos raíles paralelos, perfectamente conductores, de longitud 2L separados una distancia a, tal como se indica en la figura. Los extremos de los raíles están conectados por sendas resistencias R1 y R2. Sobre ellos se desliza una barra también perfectamente conductora de longitud $b$. La barra se desplaza con velocidad constante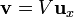 . En el espacio entre los raíles hay aplicado un campo magnético uniforme perpendicular al plano de los raíles,
. En el espacio entre los raíles hay aplicado un campo magnético uniforme perpendicular al plano de los raíles, 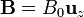 .
.
- Calcule la corriente que circula por la barra.
- Calcule la fuerza ejercida sobre la barra por el campo magnético.
- Halle la potencia disipada por efecto Joule.
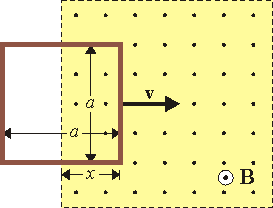
5 Frenado de espira cuadrada
Una espira cuadrada de lado , hecha de un hilo de cobre de sección
, hecha de un hilo de cobre de sección 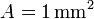 penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo
penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo 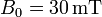 . La espira se mueve inicialmente con velocidad
. La espira se mueve inicialmente con velocidad 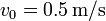 tangente a uno de sus lados y perpendicular al campo magnético. En t = 0 la espira entra en el campo.
tangente a uno de sus lados y perpendicular al campo magnético. En t = 0 la espira entra en el campo.
- Calcule la corriente que se induce en la espira cuando la espira ha avanzado una distancia
 y se está moviendo con velocidad
y se está moviendo con velocidad  .
.
- Halle la fuerza que el campo magnético ejerce con la espira.
- Si la velocidad de la espira se mantiene constante, halle la potencia disipada en la espira por efecto Joule. ¿De dónde proviene la energía disipada?
- Si se deja que la espira frene por acción del campo magnético, determine la evolución en el tiempo de la velocidad, así como la energía total disipada por efecto Joule.
6 Espira doble rotante
Se construye una espira doble, soldando una barra a una espira cuadrada de lado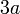 . La barra une dos lados opuestos y está situada a una distancia
. La barra une dos lados opuestos y está situada a una distancia  de uno de los lados. Tanto la barra como la espira
de uno de los lados. Tanto la barra como la espira
cuadrada están hechas de un alambre metálico de sección A y conductividad σ.
La espira gira en torno de la barra con velocidad angular ω, en el seno de un campo magnético uniforme  , perpendicular a la barra. En t = 0 el plano de la espira es perpendicular al campo magnético.
, perpendicular a la barra. En t = 0 el plano de la espira es perpendicular al campo magnético.
- Calcule la corriente que circula en cada alambre como función del tiempo.
- Halle la energía disipada en un periodo de revolución. ¿En qué se va esta energía? ¿De donde procede?
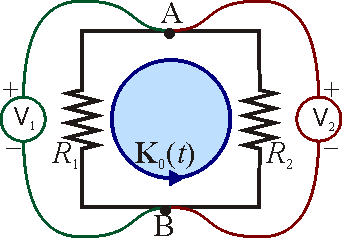
7 Circuito en torno a un solenoide
Se tiene un solenoide largo de sección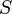 , por el cual circula una corriente variable en el tiempo K0(t). Dos voltímetros miden el voltaje entre dos puntos
, por el cual circula una corriente variable en el tiempo K0(t). Dos voltímetros miden el voltaje entre dos puntos  y
y  , diametralmente opuestos, de un circuito formado por dos resistencias
, diametralmente opuestos, de un circuito formado por dos resistencias 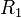 y
y 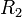 , tal como se ve en la figura. Halle las lecturas de los voltímetros. ¿Coincidirán éstas? ¿Por qué?
, tal como se ve en la figura. Halle las lecturas de los voltímetros. ¿Coincidirán éstas? ¿Por qué?
8 Espira cuadrada en torno a solenoide
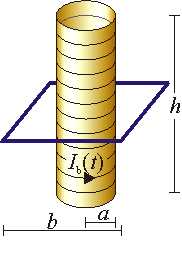
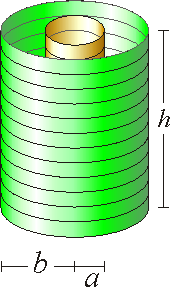
Una espira cuadrada de lado b, de resistencia R y autoinducción despreciable rodea concéntricamente a un solenoide circular largo, de radio a, de longitud h (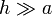 ) y N espiras. Por el solenoide circula una corriente constante Ib0, que a partir de t = 0 comienza a decaer exponencialmente como
) y N espiras. Por el solenoide circula una corriente constante Ib0, que a partir de t = 0 comienza a decaer exponencialmente como
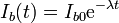
- Sabiendo que el campo magnético en el interior del solenoide es aproximadamente uniforme, calcule la corriente que circula por la espira cuadrada como función del tiempo.
- Halle la carga que pasa por un punto de la espira durante todo el periodo t > 0.
- Halle la potencia instantánea disipada por efecto Joule en la espira, así como la energía total disipada en el periodo t > 0.
- Suponga ahora la misma situación descrita anteriormente, pero considere que la espira posee una autoinducción no despreciable L y que inicialmente no circula corriente por ella. Para t > 0 la corriente que pasa por la espira es de la forma
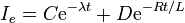
- Calcule las constantes C y D, así como la carga que pasa por un punto de la espira en el periodo t > 0 y la energía total disipada en el mismo periodo.
9 Pequeña espira junto a hilo
Un conductor cilíndrico de radio muy pequeño a y longitud indefinida es recorrido por una corriente continua I0. Una espira cuadrada muy pequeña, de lado b, resistencia R y autoinducción despreciable, es coplanaria con el hilo y se encuentra situada a una distancia y de éste (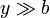 ).
).
- Calcule, detallando los pasos, el campo magnético producido por el hilo en su exterior
- Si por la espira circula una corriente I1, ¿qué fuerza ejerce el hilo sobre ella?
- Suponga que la espira se aleja del hilo, sin cambiar su orientación, de modo que y = y0 + v0t, ¿cuánto vale la corriente I1 inducida en la espira en un instante t? ¿Y la fuerza que el hilo ejerce sobre ella?
10 Espira circular en un campo variable
Una espira circular de radio  , con autoinducción
, con autoinducción  y resistencia
y resistencia  , se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
, se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
Calcule la corriente que circula por la espira si el campo magnético varía en el tiempo, durante un largo intervalo, como
11 Inducción mutua de dos anillos
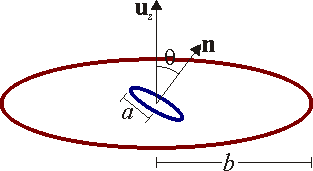
Se tienen dos anillos metálicos. Ambos anillos están centrados en el origen de coordenadas. Uno de ellos posee radio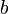 y está situado en el plano XY. El otro, de radio
y está situado en el plano XY. El otro, de radio  , está inclinado, de forma que su normal forma un ángulo
, está inclinado, de forma que su normal forma un ángulo  con el eje
con el eje  . El radio
. El radio 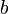 es mucho mayor que
es mucho mayor que  .
.
- Determine el coeficiente de inducción mutua entre los dos anillos a partir del flujo del campo del anillo exterior a través del anillo interior (tenga en cuenta que éste es muy pequeño) cuando por el anillo exterior circula una corriente I1.
- Halle el coeficiente de inducción mutua a partir del flujo del campo del anillo interior (que es prácticamente un dipolo) a través del anillo exterior cuando por el anillo interior circula una corriente I2. ¿Son iguales los dos coeficientes?
12 Generador de CA de dos anillos
Suponga la misma configuración geométrica del problema anterior Por el anillo exterior se hace circular una corriente constante I0. El anillo interior se hace girar en torno al diámetro común, de forma que el ángulo θ varía con velocidad constante ω.
- Despreciando los efectos de la autoinducción, halle la corriente que circula por el anillo interior.
- Calcule la energía disipada en este anillo durante un periodo de revolución.
13 Inducción mutua de dos solenoides cilíndricos
Dos solenoides cilíndricos muy largos se disponen concntricamente. Dichos solenoides poseen la misma longitud y número de espiras N1 y N2, respectivamente, las cuales están arrolladas en el mismo sentido. Los radios de las bobinas son, respectivamente, a y b (a < b).
y número de espiras N1 y N2, respectivamente, las cuales están arrolladas en el mismo sentido. Los radios de las bobinas son, respectivamente, a y b (a < b).
- Determine la matriz de inducciones mutuas del sistema.
- Calcule la constante de acoplamiento entre las bobinas.
- Suponga que se conectan el extremo superior de la bobina interior con el extremo superior de la exterior. ¿Cuál es la autoinducción equivalente de la asociación?
- Suponga que se conectan en paralelo, ¿cuál es la autoinducción equivalente de la asociación?
14 Inducción mutua de dos solenoides cuadrados
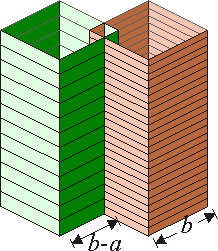
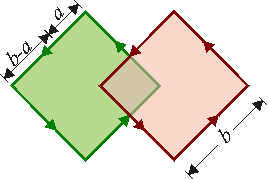
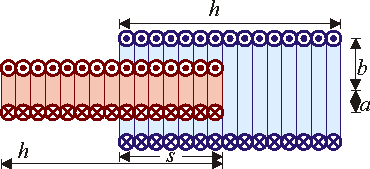
Se tienen dos solenoides de sección cuadrada de lado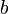 de un hilo ideal sin resistencia. La longitud de ambos solenoides es
de un hilo ideal sin resistencia. La longitud de ambos solenoides es  (
(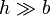 ) y el número de vueltas es N1 = N y N2 = 2N, respectivamente. Ambos solenoides se colocan de forma que intersecan en una sección cuadrada de lado a, tal como muestra la figura.
) y el número de vueltas es N1 = N y N2 = 2N, respectivamente. Ambos solenoides se colocan de forma que intersecan en una sección cuadrada de lado a, tal como muestra la figura.
- Halle los coeficientes de autoinducción, de inducción mutua y de acoplamiento.
- Sin mover los solenoides de sitio, el sistema se conecta a un circuito. Para el caso a = b / 3, halle todas las posibles autoinducciones equivalentes que se pueden obtener con este sistema, teniendo en cuenta que los solenoides pueden conectarse entre sí, cortocircuitarse con un hilo ideal o dejarse en circuito abierto.
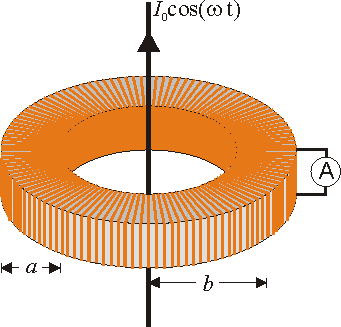
15 Amperímetro de inducción
Un amperímetro de inducción consiste en un solenoide toroidal (de resistencia despreciable y autoinducción ), que se sitúa en torno a la corriente que se pretende medir.
), que se sitúa en torno a la corriente que se pretende medir.
- Suponga un toroide de radio medio b y sección cuadrada pequeña de lado a (
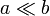 ), con N espiras arrolladas sobre un núcleo de permeabilidad μ (en este problema, ello solo supone cambiar μ0 por μ). Calcule el coeficiente de autoinducción de este solenoide, a partir del campo que se crea en su interior cuando por el solenoide circula una corriente I. Suponga que dentro del solenoide
), con N espiras arrolladas sobre un núcleo de permeabilidad μ (en este problema, ello solo supone cambiar μ0 por μ). Calcule el coeficiente de autoinducción de este solenoide, a partir del campo que se crea en su interior cuando por el solenoide circula una corriente I. Suponga que dentro del solenoide  es de la forma
es de la forma 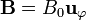 con B0 uniforme.
con B0 uniforme.
- El solenoide anterior se coloca concéntricamente con un hilo rectilíneo por el cual circula una corriente I0cos(ωt). Calcule la fuerza electromotriz que el hilo induce en el solenoide.
- Despreciando la resistencia del solenoide (pero no su autoinducción), hállese la amplitud de la corriente que circula por el solenoide.
- Esta amplitud es proporcional a la de la corriente del hilo, ¿cuánto vale la constante de proporcionalidad para un toroide de radio medio 2cm, y lado 2mm, con 300 espiras y con un núcleo de permeabilidad
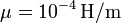 ?
?
16 Barra que cae en un campo magnético
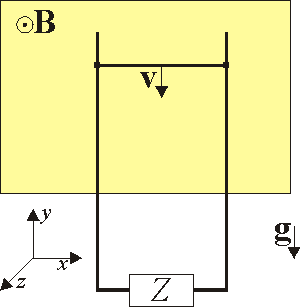
La figura representa un carril metálico superconductor por el cual puede deslizarse una varilla horizontal, también superconductora. Esta varilla está inmersa en un campo uniforme y cae por la acción de la gravedad.
y cae por la acción de la gravedad.
Inicialmente se encuentra en reposo y no circula intensidad por el circuito. En este momento se suelta. Determine la ecuación de movimiento y la posición de la varilla en función del tiempo si el circuito está cerrado por:
- Una resistencia

- Un condensador

- Una autoinducción
 .
.
Estudie en cada caso el balance energético del sistema.
17 Solenoide que se mueve en el interior de otro
Dos estrechas bobinas cilíndricas de la misma longitud , tienen radios
, tienen radios  y
y 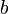 , mucho menores que su longitud
, mucho menores que su longitud  ); las bobinas son coaxiales pero se hallan desplazadas una longitud
); las bobinas son coaxiales pero se hallan desplazadas una longitud  , y están formadas por la misma cantidad de espiras compactas
, y están formadas por la misma cantidad de espiras compactas 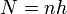 , enrolladas en el mismo sentido. Las resistencias eléctricas de las bobinas son
, enrolladas en el mismo sentido. Las resistencias eléctricas de las bobinas son 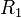 para la bobina interior y
para la bobina interior y 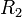 para la exterior.
para la exterior.
- Despreciando los efectos de borde, determine sus respectivos coeficientes de autoinducción L1 y L2, así como el de inducción mutua M y el de acoplamiento k.
- La bobina exterior se halla conectada a un generador de fuerza electromotriz en rampa
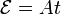 , mientras que la bobina interna se mantiene en circuito abierto. Obtenga el comportamiento en el tiempo de la intensidad I2(t) en la bobina exterior (suponga una expresión de la forma I2 = kt + c).
, mientras que la bobina interna se mantiene en circuito abierto. Obtenga el comportamiento en el tiempo de la intensidad I2(t) en la bobina exterior (suponga una expresión de la forma I2 = kt + c).
- Al mismo tiempo, la bobina interior se extrae con velocidad constante v0, de forma que s = v0t. Calcule la tensión V1(t) entre los extremos de esta bobina para t > 0.