Espira doble rotatoria
De Laplace
1 Enunciado
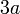. La barra une dos lados opuestos y está situada a una distancia 
de uno de los lados. Tanto la barra como la espira
cuadrada están hechas de un alambre metálico de sección A y conductividad σ.
La espira gira en torno de la barra con velocidad angular ω, en el seno de un campo magnético uniforme 
, perpendicular a la barra. En t = 0 el plano de la espira es perpendicular al campo magnético.
- Calcule la corriente que circula en cada alambre como función del tiempo.
- Halle la energía disipada en un periodo de revolución. ¿En qué se va esta energía? ¿De donde procede?
2 Corrientes en la espira
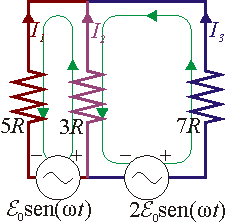
Podemos modelar este sistema como un circuito con dos mallas. Se trata de hallar la resistencia de cada rama y la fuerza electromotriz en cada malla. La aplicación de las leyes de Kirchhoff nos da la corriente en cada alambre.
Si llamamos 
a la resistencia de un tramo de longitud
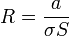
entonces el circuito está formado por tres conductores filiformes, con resistencias proporcionales a .
Para el rectángulo de anchura , la resistencia del tramo exterior es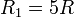 
, la de la barra común es 
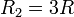. La resistencia del tramo exterior de la otra malla es 
.
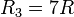La fuerza electromotriz en cada malla se obtiene aplicando la ley de Faraday.
Considerando en ambas mallas el sentido de recorrido indicado en la figura, la f.e.m. es, en cada caso
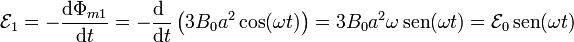
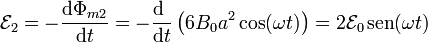
Al estar rotando el sistema en un campo uniforme, el resultado es la generación de corriente alterna en cada malla.
Aplicando ahora las leyes de Kirchhoff en cada malla obtenemos el sistema de ecuaciones
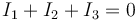
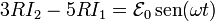
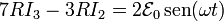
con solución
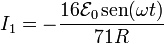
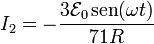
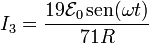
3 Energía disipada
La energía disipada en el circuito se va en forma de calor por efecto Joule, siendo la potencia disipada instantáneamente
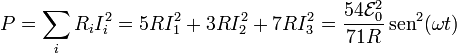
Para hallar la energía disipada en un periodo calculamos la integral
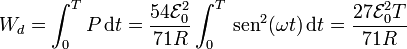
Sustituyendo el valor de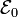 
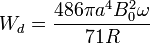
Esta energía se va en forma de calor. Es introducida en el sistema por el agente mecánico que hace girar la espira, ya que éste debe vencer las fuerzas magnéticas que el campo ejerce sobre las corrientes inducidas.
