Problemas de procesos en gases ideales (GIA)
De Laplace
| Línea 2: | Línea 2: | ||
==[[Incremento_de_energía_interna_y_trabajo_en_proceso_isóbaro_(F2GIA)|Incremento de energía interna y trabajo en proceso isóbaro]]== | ==[[Incremento_de_energía_interna_y_trabajo_en_proceso_isóbaro_(F2GIA)|Incremento de energía interna y trabajo en proceso isóbaro]]== | ||
Una cantidad fija de <math>n</math> moles de gas ideal sufre una transformación cuasiestática a presión constante <math>P_0</math>, entre el estado inicial <math>A(V_A; T_A)</math>, y el final <math>B(V_B; T_B)</math>. ¿Cuál es la variación de energía interna experimentada por el gas en el proceso? ¿Qué cantidad de trabajo se ha transferido al sistema? | Una cantidad fija de <math>n</math> moles de gas ideal sufre una transformación cuasiestática a presión constante <math>P_0</math>, entre el estado inicial <math>A(V_A; T_A)</math>, y el final <math>B(V_B; T_B)</math>. ¿Cuál es la variación de energía interna experimentada por el gas en el proceso? ¿Qué cantidad de trabajo se ha transferido al sistema? | ||
| + | |||
| + | ==[[ Comparación_de_un_proceso_isotérmico_y_uno_adiabático | Expansión isoterma y adiabática ]]== | ||
| + | Un gas ideal monoatómico ocupa un volumen de <math>4\,\mathrm{m^3}</math> | ||
| + | a la presión de <math>8\,\mathrm{atm}</math> y a la temperatura de | ||
| + | <math>400\,\mathrm{K}</math>. El gas se expande hasta la presión final de | ||
| + | <math>1\,\mathrm{atm}</math> mediante un proceso cuasiestático. Calcule el | ||
| + | trabajo realizado, el calor absorbido y la variación de energía interna en | ||
| + | los siguientes casos: | ||
| + | |||
| + | #Expansión isoterma. | ||
| + | #Expansión adiabática. | ||
== [[ Trabajo_en_un_ciclo | Trabajo en un ciclo de un gas perfecto ]] == | == [[ Trabajo_en_un_ciclo | Trabajo en un ciclo de un gas perfecto ]] == | ||
| Línea 13: | Línea 24: | ||
#Calcula el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos. | #Calcula el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| + | = Otros ejercicios = | ||
== [[ Proceso_isotermo_y_adiabático_consecutivos | Proceso isotérmico y adiabático en un gas perfecto ]] == | == [[ Proceso_isotermo_y_adiabático_consecutivos | Proceso isotérmico y adiabático en un gas perfecto ]] == | ||
Revisión de 23:43 24 may 2013
Contenido |
1 Problemas del boletín
1.1 Incremento de energía interna y trabajo en proceso isóbaro
Una cantidad fija de n moles de gas ideal sufre una transformación cuasiestática a presión constante P0, entre el estado inicial A(VA;TA), y el final B(VB;TB). ¿Cuál es la variación de energía interna experimentada por el gas en el proceso? ¿Qué cantidad de trabajo se ha transferido al sistema?
1.2 Expansión isoterma y adiabática
Un gas ideal monoatómico ocupa un volumen de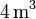 
a la presión de 
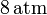y a la temperatura de
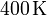. El gas se expande hasta la presión final de
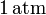mediante un proceso cuasiestático. Calcule el
trabajo realizado, el calor absorbido y la variación de energía interna en
los siguientes casos:
- Expansión isoterma.
- Expansión adiabática.
1.3 Trabajo en un ciclo de un gas perfecto
Las condiciones iniciales del estado de un gas perfecto son: V=4.00 l, P=2.00 atm, t = 27.0o C. Se dilata el gas a presión constante hasta duplicar su volumen. A continuación se comprime isotérmicamente hasta recuperar el volumen inicial. Finalmente se enfría a volumen constante hasta su presión inicial.
- Dibuja el ciclo en un diagrama PV.
- Calcula el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos.
2 Otros ejercicios
2.1 Proceso isotérmico y adiabático en un gas perfecto
Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar su presión inicial. Ambos procesos son cuasiestáticos. Halle
- La temperatura final
- El trabajo total realizado por el gas
- El calor total absorbido por el gas
- La variación de energía interna
2.2 Expansión adiabática no cuasiestática de un gas ideal
4 moles de nitrógeno están a 25 oC y 30 atm. Se pasa bruscamente la presión hasta un valor de 10 atm mediante una expansión adiabática del gas contra una presión exterior constante de 10 atm. El proceso no es cuasiestático. Calcule
- La temperatura final del gas suponiendo que la ecuación de estado de los gases ideales es aplicable a los estados inicial y final.
- La variación de energía interna.
- El trabajo realizado sobre el gas.
- Compare con las mismas magnitudes en un proceso adiabático cuasiestático que expanda el gas hasta la misma presión final de 10 atm.
