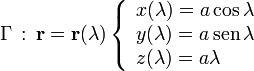|
|
| (103 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| - | = Problemas del boletín (2017/18)=
| |
| | ==[[Ecuaciones de curvas (G.I.A.)|Ecuaciones de curvas]]== | | ==[[Ecuaciones de curvas (G.I.A.)|Ecuaciones de curvas]]== |
| | Expresa en forma parámetrica e implícita las siguientes curvas | | Expresa en forma parámetrica e implícita las siguientes curvas |
| Línea 5: |
Línea 4: |
| | #Una circunferencia de radio <math>a</math>, contenida en el plano <math>XY</math> y con centro en el origen. | | #Una circunferencia de radio <math>a</math>, contenida en el plano <math>XY</math> y con centro en el origen. |
| | #Una parábola contenida en el plano <math>YZ</math> y con ecuación <math>z=y^2</math>. | | #Una parábola contenida en el plano <math>YZ</math> y con ecuación <math>z=y^2</math>. |
| - |
| |
| - | == [[Movimiento de una partícula con ecuaciones horarias dadas ]]==
| |
| - | Un cuerpo material puntual <math>P</math>, se mueve respecto de un sistema de referencia cartesiano fijo <math>OXYZ</math>. A partir del instante inicial <math>t=0</math>, dicho movimiento está descrito por las ecuaciones horarias
| |
| - | <center>
| |
| - | <math>
| |
| - | \overrightarrow{OP}(t) = \vec{r}(t) = v_0\left(t\,\vec{\imath} + \dfrac{4}{3}\dfrac{t^{3/2}}{\sqrt{T}}\,\vec{\jmath} - \sqrt{3}t\,\vec{k}\right)
| |
| - | </math>
| |
| - | </center>
| |
| - | donde <math>t</math> es el tiempo, y <math>v_0</math> y <math>T</math>, parámetros de valor conocido.
| |
| - | #Obtenga las ecuaciones de la trayectoria.
| |
| - | #Calcule los vectores velocidad y aceleración instantánea, <math>\vec{v}(t)</math> y <math>\vec{a}(t)</math>.
| |
| - | #Obtenga las expresiones intrínsecas de dichos vectores. Determine la ley horaria <math>s(t)</math> para la distancia recorrida por la partícula sobre su trayectoria, desde la posición que ocupaba en el instante inicial: es decir <math>s(t=0)=0</math>.
| |
| - | #Calcule los valores de las magnitudes cinemáticas indicadas en el apartado anterior en el instante inicial <math>t=0</math>. Discuta los resultados obtenidos.
| |
| - |
| |
| - |
| |
| - |
| |
| - | ==[[Cuestión_de_Cinemática_del_Punto,_F1_GIA_(Sept,_2012)|Cuestión sobre cinemática de la partícula]]==
| |
| - |
| |
| - | Una partícula se mueve con velocidad y aceleración instantáneas, <math>\mathbf{v}(t)</math> y <math>\mathbf{a}(t)</math>, tales que su producto escalar tiene un valor <math>k^2</math>, constante en el tiempo, y su producto vectorial es un vector <math>\mathbf{c}</math>, también constante. Considerando que el móvil parte del reposo, determine las siguientes magnitudes:
| |
| - |
| |
| - | #Ángulo que forman en cada instante las direcciones de la velocidad y la aceleración.
| |
| - | #Ley horaria <math>v(t)</math> que verifica el módulo de la velocidad instantánea (celeridad).
| |
| - | #Radio de curvatura de la trayectoria en función de la distancia <math>s</math> recorrida por la partícula, <math>R_\kappa(s)</math>.
| |
| - |
| |
| - | ==[[Parámetro arco de una hélice (G.I.A.) | Parámetro arco y triedro intrínseco de una hélice ]] ==
| |
| - | Sea la hélice <math>\Gamma</math> descrita en un sistema de referencia cartesiano <math>OXYZ</math> por las siguientes ecuaciones paramétricas:
| |
| - | <center>
| |
| - | <math>
| |
| - | \Gamma\,:\,\mathbf{r} = \mathbf{r}(\lambda)
| |
| - | \left\{
| |
| - | \begin{array}{l}
| |
| - | x(\lambda) = a \cos\lambda\\
| |
| - | y(\lambda) = a \,\mathrm{sen}\,\lambda\\
| |
| - | z(\lambda) = h \lambda
| |
| - | \end{array}
| |
| - | \right.
| |
| - | </math>
| |
| - | </center>
| |
| - | donde <math>a</math> y <math>h</math> son constantes conocidas.
| |
| - | #Determina la longitud recorrida sobre la hélice (parámetro arco) en función del parámetro <math>\lambda</math>
| |
| - | #Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
| |
| - | #Calcula su radio de curvatura.
| |
| - |
| |
| - |
| |
| - | ==[[Cuestión de cinemática del punto, Noviembre 2012 (F1 GIA) |Movimiento instantáneo de una partícula]]==
| |
| - | Una partícula <math>P</math> se mueve respecto de un sistema de referencia cartesiano <math>OXYZ</math> de manera que en un cierto instante <math>t_0</math>, su velocidad <math>\vec{v}</math> y su aceleración <math>\vec{a}</math> están descritas por los vectores
| |
| - |
| |
| - | <center><math>\vec{v}=\vec{\imath}+\sqrt{3}\!\ \vec{k}\quad\mathrm{y}\quad\vec{a}=\vec{\imath}+\sqrt{5}\vec{\jmath}-\sqrt{3}\!\ \vec{k}\mathrm{,}</math></center>
| |
| - |
| |
| - | con sus componentes medidas en <math>\mathrm{m}/\mathrm{s}</math> y <math>\mathrm{m}/\mathrm{s}^2</math>, respectivamente. Determine, en el instante considerado, las siguientes magnitudes cinemáticas:
| |
| - |
| |
| - | #Módulo de la velocidad (celeridad) y su derivada.
| |
| - | #Componente normal de la aceleración y radio de curvatura de la trayectoria.
| |
| - | #Vector aceleración normal.
| |
| - |
| |
| - | ==[[Velocidad de un punto en la superficie de la Tierra (G.I.A.) | Velocidad de un punto en la superficie de la Tierra ]]==
| |
| - | La Tierra rota uniformemente con respecto a su eje con velocidad angular <math>\omega</math> constante. Encuentra en función de
| |
| - | la latitud <math>\lambda</math>, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: <math>R = 6.37 \times 10^6</math> m.)
| |
| - |
| |
| - | ==[[F1 GIA PPC 2013, Punto moviéndose en una circunferencia sobre un plano | Partícula describiendo una circunferencia en plano]]==
| |
| - | [[Imagen:F1_GIA_PPC_2013_circulo_sobre_plano_girado.png|right]]
| |
| - | Un punto material <math>P</math> se mueve recorriendo la circunferencia <math>\Gamma</math> contenida en un plano fijo <math>\Pi</math> y cuyo centro es el punto <math>C</math>, dado por el segmento orientado <math>\overrightarrow{OC} = \vec{\jmath} + \vec{k}</math>, cuyas componentes se miden en metros (m) y están referidas a un sistema cartesiano <math>OXYZ</math>. En el instante inicial <math>(t = 0)</math>, el punto móvil <math>P</math> ocupa la posición determinada por el segmento orientado <math>\overrightarrow{OP}_0 = 2\,\vec{\jmath}</math>. A partir de ́esta, la partícula realiza un movimiento circular caracterizado por un vector rotación instantánea o velocidad angular, cuyas componentes
| |
| - | medidas en radianes por segundo son:
| |
| - | <center>
| |
| - | <math>
| |
| - | \vec{\omega}(t) = \cos(\omega_0t)\left(\vec{\imath} + 2\,\vec{\jmath} + 2\vec{k}\right) \,\mathrm{(rad/s)}; \quad \mathrm{con}\quad
| |
| - | \omega_0 = \dfrac{3}{2\pi}\,\mathrm{rad/s}
| |
| - | </math>
| |
| - | </center>
| |
| - | El movimiento se verifica en el intervalo de tiempo <math>0 \leq t \leq \pi/2\omega_0</math> , de manera que la partícula recorre la circunferencia una sola vez, y siempre en sentido antihorario.
| |
| - | #¿Cómo es la ley horaria <math>\theta(t)</math> que describe el ́angulo recorrido por el segmento orientado <math>\overrightarrow{CP} </math>, desde el instante inicial hasta el instante <math>t </math>?
| |
| - | #¿Cómo es el vector binormal del triedro intrínseco a la trayectoria, en función de la posición de la partícula?
| |
| - | #¿Cómo es la curvatura de la trayectoria durante el movimiento?
| |
| - | #¿Cómo es la velocidad instantánea de la partícula en <math>t=0 </math>?
| |
| - | #Calcule las componentes tangencial y normal de la velocidad en el instante inicial
| |
| - |
| |
| - | ==[[Movimiento oscilatorio armónico unidimensional | Movimiento oscilatorio armónico unidimensional]]==
| |
| - | Un punto inicialmente en reposo en la posición <math>x=L</math> describe un movimiento rectilíneo sobre el eje <math>OX</math>, de modo que su aceleración es de la forma <math>a = -k^2x</math>. Determina en función del tiempo su posición y velocidad. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?
| |
| - |
| |
| - | = Otros problemas resueltos=
| |
| | | | |
| | ==[[Trayectoria de una partícula (G.I.A.)|Trayectoria de una partícula]]== | | ==[[Trayectoria de una partícula (G.I.A.)|Trayectoria de una partícula]]== |
| Línea 95: |
Línea 14: |
| | Determina la velocidad y aceleración de la partícula, los vectores del triedro intrínseco, así como la ecuación de la trayectoria. Calcula también las componentes intrínsecas de la velocidad y la aceleración ¿Cual es la expresión de un desplazamiento elemental <math>\mathrm{d}\vec{r}</math>? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula. | | Determina la velocidad y aceleración de la partícula, los vectores del triedro intrínseco, así como la ecuación de la trayectoria. Calcula también las componentes intrínsecas de la velocidad y la aceleración ¿Cual es la expresión de un desplazamiento elemental <math>\mathrm{d}\vec{r}</math>? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula. |
| | | | |
| - | ==[[Partícula con magnitudes cinemáticas dependientes del parámetro arco]]== | + | ==[[Tiro oblicuo (G.I.A.)| Tiro oblicuo ]]== |
| - | Una partícula se mueve describiendo una trayectoria cuyo radio de curvatura <math>R_{\kappa}</math> es proporcional a la
| + | Determina el movimiento de un proyectil disparado con una velocidad inicial <math>v_0</math> y un ángulo <math>\alpha</math> con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria. |
| - | distancia <math>s</math> que aquélla ha recorrido sobre la trayectoria. Además, se comprueba que el módulo de
| + | |
| - | la velocidad de la partícula (celeridad), <math>v=|\vec{v}|</math>, es proporcional a la raíz cuadrada del valor de dicha | + | |
| - | distancia <math>s</math>. ¿Cómo es el módulo de la aceleración instantánea de la partícula, <math>a=|\vec{a}|</math>?
| + | |
| | | | |
| - | ==[[Partícula con curvatura y aceleración tangencial dependientes del tiempo, Noviembre 2014 (G.I.C.)| Partícula con curvatura y aceleración tangencial dependientes del tiempo]]== | + | ==[[Cuerda enrollándose (G.I.A.)| Cuerda enrollándose]]== |
| - | Una partícula se mueve de modo que, en todo instante, su curvatura es <math>\kappa = At</math> y su aceleración tangencial es <math>a_T=Bt</math>, siendo <math>A</math> y <math>B</math> constantes. Suponemos que en el instante inicial la partícula está en reposo.
| + | |
| - | #¿Cuáles son las unidades base de las constantes en el SI?
| + | |
| - | #Suponiendo que en <math>t=0</math> se tiene <math>s=0</math>, calcula la distancia recorrida en cada instante de tiempo
| + | |
| - | #Calcula el módulo de la aceleración en cada instante.
| + | |
| | | | |
| - | ==[[Barra con extremos sobre los ejes, Enero 2012 (G.I.C.)|Barra con extremos sobre los ejes]]==
| |
| - | [[Imagen:F1_GIC_barra_con_extremos_sobre_ejes_enunciado.png|right]]
| |
| - | Dos partículas, <math>A</math> y <math>B</math>, de masa <math>m</math>, están unidas por una barra rígida de longitud <math>L</math> y masa despreciable.
| |
| - | La partícula <math>A</math> se mueve sobre el eje <math>OX</math> con velocidad uniforme <math>v_0</math>, mientras que la partícula <math>B</math> está obligada a moverse
| |
| - | sobre el eje <math>OY</math>. Si en el instante <math>t=0</math> la partícula <math>A</math> se encontraba en el punto <math>O</math>
| |
| - | #Encuentra la posición, velocidad y aceleración de la partícula <math>B</math> en función de <math>v_0</math> y del tiempo.
| |
| - | #¿Cuál es el vector de posición y la velocidad del punto medio de la barra (<math>C</math>) en función de <math>v_0</math> y <math>t_0</math>?
| |
| - | #Describe la curva que corresponde a la trayectoria del punto medio de la barra.
| |
| - | #¿Que tipo de movimiento describe el punto medio de la barra? Razona tu respuesta.
| |
| - |
| |
| - | ==[[Barra girando en un plano (G.I.A.)|Barra girando en un plano]]==
| |
| - | [[Imagen:F1_GIA_p04_05_a.png|right]]
| |
| - | Una barra rígida <math>AB</math> de longitud <math>\ a\ </math> se mueve en un plano
| |
| - | vertical <math>OXY</math>, manteniendo su extremo <math>A</math> articulado en un punto
| |
| - | del eje horizontal de coordenadas <math>\overrightarrow{OA}= a \vec{\imath}</math>, y
| |
| - | verificando la ley horaria <math>\theta (t) = 2 \omega t</math>, con <math>0 \leq
| |
| - | \theta \leq \pi</math> y siendo <math>\omega=</math>cte. Un hilo inextensible de
| |
| - | longitud <math>2a</math> tiene uno de sus extremos conectado al origen del
| |
| - | sistema de referencia (punto <math>O</math>), mientras que del otro cuelga
| |
| - | una partícula <math>P</math> que mantiene al hilo siempre tenso. El hilo se
| |
| - | apoya sobre una pequeña polea de radio despreciable situada en el
| |
| - | extremo <math>B</math> de la barra, de forma que el tramo <math>\overline{BP}</math>
| |
| - | permanece siempre paralelo al eje <math>OY</math> (ver figura). Se pide:
| |
| - | #Ecuaciones horarias del punto <math>P: \ \overrightarrow{OP} = \mathbf{r} (t) =x(t) \vec{\imath} + y(t) \vec{\jmath}</math>.
| |
| - | #Instante del tiempo <math>t_M</math> en que la partícula alcanza su altura máxima.
| |
| - | #Radio de curvatura de la trayectoria seguida por <math>P</math>, en el instante considerado en el apartado anterior.
| |
| - |
| |
| - | ==[[Barra deslizando sobre una circunferencia (G.I.A.) | Barra deslizando sobre una circunferencia ]]==
| |
| - | [[Imagen:F1_GIA_p04_08_a.png|right]]
| |
| - | En un plano <math>OXY</math>, se define el sistema cinemático formado por los dos siguientes elementos geométricos:
| |
| - | #una circunferencia fija, de radio <math>R</math> y centrada en el punto <math>C</math> de coordenadas <math>(x_C=R,\, y_C=0)</math>;
| |
| - | #un segmento rectilíneo móvil <math>A'A</math>, de longitud superior a <math>4R</math>, el cual gira con velocidad angular constante <math>\omega</math> (en sentido antihorario) alrededor de un eje fijo que pasa por su punto medio <math>O</math> y es normal al plano <math>OXY</math> (eje <math>OZ</math>).
| |
| - | Sabiendo que el ángulo <math>\theta</math> ( que forman <math>OA</math> y <math>OX</math>) es nulo en
| |
| - | el instante inicial <math>(t=0)</math>; y considerando como móvil problema el
| |
| - | punto <math>P</math> en el que se cortan el segmento <math>A'A</math> y la circunferencia , se pide:
| |
| - | #item Determinar las ecuaciones horarias, <math>\mathbf{r}(t) = \overrightarrow{OP}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}</math>, del punto <math>P</math>, así como sus vectores velocidad, <math>\mathbf{v}(t)</math>, y aceleración, <math>\mathbf{a}(t)</math>.
| |
| - | #Calcular las aceleraciones tangencial y normal de dicho punto <math>P</math>.
| |
| - | ==[[Cuerda enrollándose (G.I.A.)| Cuerda enrollándose]]==
| |
| - | [[Imagen:F1_GIA_p04_04_a.png|right]]
| |
| | Una partícula se mueve en el plano <math>OXY</math> mientras permanece | | Una partícula se mueve en el plano <math>OXY</math> mientras permanece |
| | conectada a uno de los extremos de un hilo inextensible de longitud | | conectada a uno de los extremos de un hilo inextensible de longitud |
| Línea 163: |
Línea 36: |
| | #El triedro intrínseco de la trayectoria seguida por la partícula | | #El triedro intrínseco de la trayectoria seguida por la partícula |
| | | | |
| - | ==[[Cuerda sobre disco de radio variable | Cuerda sobre disco de radio variable]]==
| |
| - | [[Imagen:Circunferencia_radio_variable_enunciado.png|right]]
| |
| - | Un punto material <math>P</math> pende verticalmente del extremo de un hilo inextensible y permanentemente tenso. Este se apoya y desliza sobre una circunferencia de radio variable con el tiempo <math>R(t) = R_0\,\mathrm{sen}\,(\omega t)</math> en el intervalo <math>0\leq t\leq\pi/2\omega</math> (<math>R_0</math> y <math>\omega</math> son constantes conocidas), y centrada en el origen <math>O</math> de un sistema de referencia cartesiano <math>OXY</math> . La longitud total del hilo es <math>l = \pi R_0 /2</math>, y su otro extremo se halla fijo en un punto <math>A</math>, tal que <math>\overrightarrow{OA} = R_0 \,\vec{\jmath}</math> (ver figura). Determina:
| |
| - | #Las ecuaciones horarias cartesianas del punto <math>P</math> , y su posición final en el instante final <math>t_f = \pi/2\omega</math>.
| |
| - | #Los vectores velocidad y aceleración de dicho punto en todo instante de tiempo.
| |
| - | #La aceleración normal de <math>P</math> y el radio de curvatura de su trayectoria en todo instante de tiempo, así como la posición del centro de curvatura de la trayectoria en el instante inicial.
| |
| | | | |
| | + | ==[[Barra girando en un plano (G.I.A.)|Barra girando en un plano]]== |
| | + | Una barra rígida <math>AB</math> de longitud <math>\ a\ </math> se mueve en un plano |
| | + | vertical <math>OXY</math>, manteniendo su extremo <math>A</math> articulado en un punto |
| | + | del eje horizontal de coordenadas <math>\overrightarrow{OA}= a \vec{\imath}</math>, y |
| | + | verificando la ley horaria <math>\theta (t) = 2 \omega t</math>, con <math>0 \leq |
| | + | \theta \leq \pi</math> y siendo <math>\omega=</math>cte. Un hilo inextensible de |
| | + | longitud <math>2a</math> tiene uno de sus extremos conectado al origen del |
| | + | sistema de referencia (punto <math>O</math>), mientras que del otro cuelga |
| | + | una partícula <math>P</math> que mantiene al hilo siempre tenso. El hilo se |
| | + | apoya sobre una pequeña polea de radio despreciable situada en el |
| | + | extremo <math>B</math> de la barra, de forma que el tramo <math>\overline{BP}</math> |
| | + | permanece siempre paralelo al eje <math>OY</math> (ver figura). Se pide: |
| | + | #Ecuaciones horarias del punto <math>P: \ \overrightarrow{OP} = \mathbf{r} (t) =x(t) \vec{\imath} + y(t) \vec{\jmath}</math>. |
| | + | #Instante del tiempo <math>t_M</math> en que la partícula alcanza su altura máxima. |
| | + | #Radio de curvatura de la trayectoria seguida por <math>P</math>, en el instante considerado en el apartado anterior. |
| | | | |
| - | ==[[Cuestión de cinemática, Noviembre 2011 |Disco girando con partícula suspendida de cuerda]]== | + | ==[[Velocidad de un punto en la superficie de la Tierra (G.I.A.) | Velocidad de un punto en la superficie de la Tierra ]]== |
| - | [[Archivo:cinem_nov_11.gif|right]]El mecanismo de la figura consiste en un disco de radio <math>R</math>, siempre contenido en el plano vertical <math>OXY</math>, que se mueve girando alrededor de un punto de su perímetro que coincide con el origen <math>O</math> del sistema de referencia. El movimiento del disco está descrito por la ley horaria <math>\theta(t)</math> para el ángulo (medido en radianes) que forma el diámetro <math>\overline{OD}</math> con la dirección horizontal <math>OX</math>. Se considera que el sistema parte de la posición inicial <math>\theta=0</math>. En el punto <math>D</math> hay conectada una cuerda flexible e inextensible de longitud <math>L=\pi R</math> que, cuando el disco gira, se va enrollando sobre su contorno, finalizando el proceso cuando <math>\theta=\pi</math>. Además, un punto material pesado <math>P</math> hace que el tramo de cuerda no enrollado siempre penda verticalmente.
| + | La Tierra rota uniformemente con respecto a su eje con velocidad angular <math>\omega</math> constante. Encuentra en función de |
| | + | la latitud <math>\lambda</math>, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: <math>R = 6.37 \times 10^6</math> m.) |
| | | | |
| - | # Obtenga la ecuación paramétrica de la trayectoria <math>\Gamma</math>.
| |
| - | # El extremo <math>D</math> del diámetro realiza un movimiento circular uniforme, siendo su aceleración <math>8R\omega_0^2</math>. ¿Cómo es la correspondiente ley horaria para el ángulo <math>\theta</math>?
| |
| - | # Calcule la expresión de la componente intrínseca de la velocidad de la partícula <math>P</math>.
| |
| - | # Aceleración tangencial del punto <math>P</math>.
| |
| - | # Radio de curvatura de la trayectoria de <math>P</math> en el punto de inicial.
| |
| | | | |
| | ==[[Punto moviéndose sobre una parábola (G.I.A.) | Punto moviéndose sobre una parábola]]== | | ==[[Punto moviéndose sobre una parábola (G.I.A.) | Punto moviéndose sobre una parábola]]== |
| - | | + | Un punto inicialmente en reposo en la posición <math>x=a</math>, <math>y=b</math>, |
| - | [[Archivo:problema_9_11_12_peq.gif|right]]Un punto inicialmente en reposo en la posición <math>x=a</math>, <math>y=b</math>,
| + | |
| | describe la parábola <math>\ \Gamma: y^2 = (b^2/a) x</math>. Se conoce la | | describe la parábola <math>\ \Gamma: y^2 = (b^2/a) x</math>. Se conoce la |
| | componente <math>y</math> de la aceleración: <math>a_y =- k^2 y</math>, con <math>k=cte</math>. | | componente <math>y</math> de la aceleración: <math>a_y =- k^2 y</math>, con <math>k=cte</math>. |
| Línea 189: |
Línea 66: |
| | tiempo tarda en alcanzarla? | | tiempo tarda en alcanzarla? |
| | | | |
| | + | ==[[Barra deslizando sobre una circunferencia (G.I.A.) | Barra deslizando sobre una circunferencia ]]== |
| | + | En un plano <math>OXY</math>, se define el sistema cinemático formado por los dos siguientes elementos geométricos: |
| | + | #una circunferencia fija, de radio <math>R</math> y centrada en el punto <math>C</math> de coordenadas <math>(x_C=R,\, y_C=0)</math>; |
| | + | #un segmento rectilíneo móvil <math>A'A</math>, de longitud superior a <math>4R</math>, el cual gira con velocidad angular constante <math>\omega</math> (en sentido antihorario) alrededor de un eje fijo que pasa por su punto medio <math>O</math> y es normal al plano <math>OXY</math> (eje <math>OZ</math>). |
| | + | Sabiendo que el ángulo <math>\theta</math> ( que forman <math>OA</math> y <math>OX</math>) es nulo en |
| | + | el instante inicial <math>(t=0)</math>; y considerando como móvil problema el |
| | + | punto <math>P</math> en el que se cortan el segmento <math>A'A</math> y la circunferencia , se pide: |
| | + | #item Determinar las ecuaciones horarias, <math>\mathbf{r}(t) = \overrightarrow{OP}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}</math>, del punto <math>P</math>, así como sus vectores velocidad, <math>\mathbf{v}(t)</math>, y aceleración, <math>\mathbf{a}(t)</math>. |
| | + | #Calcular las aceleraciones tangencial y normal de dicho punto <math>P</math>. |
| | | | |
| - | ==[[Tiro oblicuo (G.I.A.)| Tiro oblicuo ]]==
| |
| - | Determina el movimiento de un proyectil disparado con una velocidad inicial <math>v_0</math> y un ángulo <math>\alpha</math> con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria.
| |
| | | | |
| - | ==[[F1 GIA PPC 2013, Cañon lanzando partícula sobre un carrito deslizando sobre plano inclinado | Cañon lanzando partícula sobre un carrito deslizando sobre plano inclinado]]== | + | ==[[Parámetro arco de una hélice (G.I.A.) | Parámetro arco de una hélice ]] == |
| - | [[Imagen:F1_GIA_PPC_2013_canon_carrito_plano_inclinado.png|right]]
| + | Sea la hélice <math>\Gamma</math> descrita en un sistema de referencia cartesiano <math>OXYZ</math> por las siguientes ecuaciones paramétricas: |
| - | Un móvil <math>A </math>, que puede ser considerado como un cuerpo puntual, se desplaza por una ladera con una pendiente de <math>45^{o} </math> respecto de la horizontal. El móvil desciende por la ladera realizando un movimiento rectilíneo uniformemente acelerado, siendo el módulo de su aceleración <math>|\vec{a}_0|=a_0=g/\sqrt{2} </math>. En el instante de iniciar el descenso el móvil se encuentra en reposo, a una altura <math>d </math>. Además, a una distancia <math>d </math> de la base de la ladera, en dirección horizontal, se halla emplazado un dispositivo lanzador de proyectiles a los que imprime una velocidad inicial de módulo <math>v_0 </math> y formando un ángulo <math>\alpha </math> con la horizontal.
| + | |
| - | #Encuentre la expresión de las ecuaciones horarias que describen el movimiento del móvil <math>A </math> respecto al sistema de referencia del dibujo.
| + | |
| - | #En el instante en el que el móvil <math>A </math> inicia el descenso, el lanzado dispara un proyectil <math>B </math> que, a partir de entonces, se mueve con la aceleración debida a la acción de la gravedad, <math>\vec{g} = -g\,\vec{\jmath} </math>, constante en módulo, dirección y sentido. ¿Qué valores deben tener el ángulo de lanzamiento <math>\alpha </math> y la celeridad inicial <math>v_0 </math> del proyectil <math>B </math> para que éste impacte sobre el móvil <math>A </math> cuando se encuentra en la mitad de la ladera?
| + | |
| - | | + | |
| - | ==[[Tiro parabólico sobre un plano inclinado, Diciembre 2012 (G.I.C.)| Tiro parabólico sobre un plano inclinado]]==
| + | |
| - | [[Imagen:F1_GIC_tiro_parabolico_sobre_plano_inclinado_enunciado.png|right]]
| + | |
| - | Se tiene el plano inclinado de la figura que forma un ángulo <math>\pi/4</math> con la horizontal.
| + | |
| - | se dispara una partícula desde el punto más bajo, con una velocidad inicial
| + | |
| - | <math>\vec{v}_0</math>, de módulo <math>v_0</math> y con un ángulo <math>\alpha</math> con la horizontal.
| + | |
| - | #Calcula la distancia entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
| + | |
| - | #Calcula el trabajo realizado por la fuerza gravitatoria a lo largo de la trayectoria de la partícula, así como la potencia que la fuerza gravitatoria transmite a la partícula en cada instante.
| + | |
| - | #Para el caso <math>\alpha=\pi/3</math>, calcula las componentes intrínsecas de la aceleración en el punto de impacto y el radio de curvatura.
| + | |
| - | | + | |
| - | ==[[Partícula recorriendo una espiral, Enero 2014 (G.I.C.) | Partícula recorriendo una espiral]]==
| + | |
| - | Una partícula recorre una espiral logarítmica con coordenadas polares <math>r(t) = a\,e^{\theta(t)}</math>, donde <math>\theta(t) = \omega t</math>,
| + | |
| - | Aquí, <math>t</math> es el tiempo y <math>a</math> y <math>\omega</math> son constantes. Encuentra la expresión del vector de posición en coordenadas polares
| + | |
| - | y del triedro intrínseco en cada punto de la trayectoria en función del tiempo. Determina la ley horaria <math>s(t)</math> que da la
| + | |
| - | distancia recorrida por la partícula en función del tiempo.
| + | |
| - | | + | |
| - | ==[[Partícula moviéndose sobre una parábola, Noviembre 2014 (G.I.C.)| Partícula moviéndose sobre una parábola]]==
| + | |
| - | | + | |
| - | Una partícula se mueve siguiendo la trayectoria descrita por la curva de
| + | |
| - | ecuaciones implícitas <math>y=A(1-x^2/A^2)</math> y <math>z=0</math>, donde <math>A</math> es una constante. La
| + | |
| - | coordenada <math>x</math> varía en el intervalo <math>x\in[0,A]</math>.
| + | |
| - | #Determina el vector tangente en función de la posición de la partícula
| + | |
| - | #Suponiendo que en <math> t=0</math> la distancia recorrida es <math>s=0 </math> encuentra la expresión que da la distancia total recorrida sobre la curva.
| + | |
| - | #¿Cuál es el vector normal a la trayectoria en <math>x=0 </math>?
| + | |
| - | | + | |
| - | ==[[F1 GIA PPC 2014, Partícula moviéndose sobre una parábola | Partícula moviéndose sobre una parábola]]==
| + | |
| - | [[Imagen:F1_GIA_PPC_2014_parabola.png|right]]
| + | |
| - | Una partícula <math>P</math> realiza un movimiento en el plano <math>OXY</math> , cuya trayectoria <math>\Gamma</math>, y ley horaria para la
| + | |
| - | coordenada <math>y = y(t)</math>, están descritas por las expresiones:
| + | |
| | <center> | | <center> |
| | <math> | | <math> |
| - | \Gamma: x = \dfrac{1}{4b}y^2; \qquad y(t) = 2b-v_0t | + | \Gamma\,:\,\mathbf{r} = \mathbf{r}(\lambda) |
| - | </math>
| + | |
| - | </center>
| + | |
| - | siendo <math>b</math> y <math>v_0</math> constantes de valor positivo conocido. El movimiento se inicia en el instante <math>t=0</math>, cuando la partícula ocupa la posición de coordenadas <math>P_0(b,2b)</math>, y termina en la posición <math>P_f(b,-2b)</math>.
| + | |
| - | | + | |
| - | # Obtenga una expresión paramétrica de <math>\overrightarrow{OP}=\vec{r}(\lambda)</math> de la trayectoria <math>\Gamma</math> de la partícula
| + | |
| - | # Calcule el vector tangente a la trayectoria en un punto de coordenadas <math>P(x,y)</math>
| + | |
| - | #Sea <math>s(t)</math> la distancia medida a lo largo de la trayectoria, desde <math>P_0</math> hasta el punto en que se encuentra la partícula en el instante <math>t</math>. Obtenga la expresión de la distancia que por unidad de tiempo recorre la partícula en dicho instante,<math>
| + | |
| - | \dot{s}(t)</math>
| + | |
| - | #¿En qué puntos de la trayectoria se anula la componente tangencial y/o la componente normal de la aceleración?
| + | |
| - | | + | |
| - | | + | |
| - | ==[[Partícula moviéndose sobre una hélice, Enero 2015 (F1 GIA)| Partícula moviéndose sobre una hélice]]==
| + | |
| - | [[Imagen:G1_GIA_PPC_2015_particula_sobre_helice_enunciado.png|right]]
| + | |
| - | Una partícula <math>P </math> de masa <math>m </math> está insertada en la hélice fija y uniforme <math>\Gamma </math>. Utilizando un sistema de referencia cartesiano <math>OXYZ </math>, en el cuál la gravedad está descrita analíticamente por el vector <math>\vec{g}=-g\vec{k} </math>, la ecuación parámetrica de dicha hélice es:
| + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | \Gamma:\vec{r}(\theta) = x(\theta)\,\vec{\imath} + y(\theta)\,\vec{\jmath} + z(\theta)\,\vec{k}
| + | |
| | \left\{ | | \left\{ |
| - | \begin{array}{l} | + | \begin{array}{l} |
| - | x(\theta) = a\cos\theta\\ | + | x(\lambda) = a \cos\lambda\\ |
| - | \\ | + | y(\lambda) = a \,\mathrm{sen}\,\lambda\\ |
| - | y(\theta) = a\,\mathrm{sen}\,\theta\\ | + | z(\lambda) = a \lambda |
| - | \\ | + | \end{array} |
| - | z(\theta) = \lambda\,\theta | + | |
| - | \end{array} | + | |
| | \right. | | \right. |
| | </math> | | </math> |
| | </center> | | </center> |
| - | donde <math>a </math> y <math>\lambda </math> son constantes. EL parámetro geométrico <math>\theta </math> es el ángulo que forma con el eje <math>OX </math> la proyección del radio-vector <math>\vec{r}=\overrightarrow{OP} </math> sobre el plano horizontal <math>OXY </math>. Cuando la partícula recorre la hélice <math>\Gamma </math>, sin rozamiento apreciable, su movimiento queda descrito por la ley horaria <math>\theta(t) </math>. | + | donde <math>a</math> y <math>h</math> son constantes conocidas. |
| - | #Determine cuál debe ser el valor de la constante <math>\lambda </math> para que el radio de curvatura de la hélice sea <math>R_{\kappa}=3a/2 </math>. ¿Qué distancia <math>h </math> asciende la partícula en la dirección vertical cada vez que da una vuelta completa alrededor del eje <math>OZ </math>. | + | #Determina el parámetro arco de la hélice descrita. |
| - | #Obtenga la expresiones de las componentes intrínsecas de la velocidad y la aceleración en términos de la ley horaria <math>\theta(t) </math> y/o sus derivadas. | + | #Obtén los vectores del triedro intrínseco en cada punto de dicha curva. |
| - | | + | #Calcula su radio de curvatura. |
| - | ==[[Partícula en movimiento con trayectoria y ley horaria conocidas, Enero 2018 (F1 GIA)| Partícula en movimiento con trayectoria y ley horaria conocidas]]==
| + | |
| - | Una partícula <math>P</math> se mueve respecto de un sistema de referencia cartesiano <math>OXYZ</math>, recorriendo la curva <math>\Gamma</math> descrita por la ecuación paramétrica:
| + | |
| - | | + | |
| - | <center><math>\Gamma: \!\ \vec{r}(\varphi)= b\!\ \bigg(\cos^2 \varphi
| + | |
| - | \!\ \vec{\imath}+\,\mathrm{sen}^2\,
| + | |
| - | \varphi\!\ \vec{\jmath}\!\ +\frac{1}{\sqrt{2}}\ \,\mathrm{sen} 2\varphi\!\ \vec{k}\bigg)
| + | |
| - | </math></center>
| + | |
| - | | + | |
| - | El movimiento de la partícula tiene lugar en el intervalo <math>0\leq \varphi(t) \leq 2\pi</math>, según la ley horaria <math>\varphi(t)=\omega_0\!\ t</math>. Los parámetros <math>b</math> y <math>\omega_0</math> tienen valores constantes conocidos.
| + | |
| - | | + | |
| - |
| + | |
| - | | + | |
| - | Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria <math>\displaystyle s(t)</math> para el parámetro arco.
| + | |
| - | | + | |
| - | | + | |
| - | = Problemas propuestos =
| + | |
| - | | + | |
| - | == [[Otro movimiento de una partícula con ecuaciones horarias dadas ]]==
| + | |
| - | | + | |
| - | Las ecuaciones horarias del movimiento de una partícula <math>P</math>,
| + | |
| - | descritas respecto de un sistema de referencia cartesiano <math>OXY</math>,
| + | |
| - | están dadas por las siguientes expresiones:
| + | |
| - | | + | |
| - | <center><math> \overrightarrow{OP}(t) = \vec{r} (t)=x(t) \vec{\imath}+y(t) \vec{\jmath}+z(t) \vec{k}\mathrm{;}\;\; \left\{
| + | |
| - | \begin{array}{l}
| + | |
| - | \displaystyle x (t) = v_0\!\ t \cos \omega t - \frac{v_0}{\omega} \mathrm{sen}\!\ \omega t \\
| + | |
| - | \\ \displaystyle y (t) = v_0\!\ t \mathrm{sen}\!\ \omega t + \frac{v_0}{\omega} \cos \omega
| + | |
| - | t\\ \\ \displaystyle z(t)=\frac{1}{2}\ v_0\omega\!\ t^2
| + | |
| - | \end{array} \right. </math></center>
| + | |
| - | | + | |
| - | donde <math>t</math> es la variable tiempo, y <math>v_0</math> y <math>\omega</math>, parámetros con valores conocidos. Obtenga las expresiones de las siguientes magnitudes cinemáticas y propiedades de la trayectoria:
| + | |
| - | # Vectores velocidad y aceleración en función del tiempo <math>\vec{v}(t)</math> y <math>\vec{a}(t)</math>, respectivamente. | + | |
| - | # Componentes intrínsecas de la velocidad y de la aceleración, en función del tiempo. ¿Cómo es el radio de curvatura de la trayectoria en el punto ocupado por la partícula en un instante <math>t</math> arbitrario?
| + | |
| - | # Distancia <math>s(t)</math> recorrida por la partícula <math>P</math> sobre la trayectoria, expresada en función del tiempo y medida a partir de la posición inicial de la partícula; es decir, <math>s(t=0)=0</math>. Obtenga la expresión del radio de curvatura de la trayectoria, en función de la distancia <math>s</math> al punto inicial.
| + | |
| - | | + | |
| - | [[Categoría:Problemas de Cinemática del Punto F1 GIA]]
| + | |
| - | [[Categoría:Cinemática del punto material|1]]
| + | |
| - | [[Categoría:Física I (G.I.A.)]]
| + | |
| - | [[Categoría:Física I (G.I.T.I.)]]
| + | |
Determina la velocidad y aceleración de la partícula, los vectores del triedro intrínseco, así como la ecuación de la trayectoria. Calcula también las componentes intrínsecas de la velocidad y la aceleración ¿Cual es la expresión de un desplazamiento elemental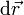 
? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula.
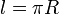. El otro extremo está unido a un punto fijo A de una
circunferencia de radio R y centro O, cuyas coordenadas en el
sistema cartesiano OXY son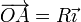 
. Partiendo
de la posición inicial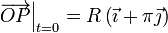 
, el movimiento de la partícula con velocidad de módulo
constante v0 da lugar a que el hilo, que permanece siempre tenso,
se enrolle en dicha circunferencia. Utilizando como parámetro el
ángulo θ correspondiente al punto C donde desaparece el
contacto hilo--circunferencia, calcula:
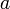se mueve en un plano
vertical OXY, manteniendo su extremo A articulado en un punto
del eje horizontal de coordenadas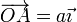 
, y
verificando la ley horaria θ(t) = 2ωt, con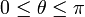 
y siendo ω = cte. Un hilo inextensible de
longitud 2a tiene uno de sus extremos conectado al origen del
sistema de referencia (punto O), mientras que del otro cuelga
una partícula P que mantiene al hilo siempre tenso. El hilo se
apoya sobre una pequeña polea de radio despreciable situada en el
extremo B de la barra, de forma que el tramo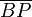 
permanece siempre paralelo al eje OY (ver figura). Se pide:
.
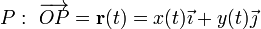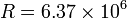m.)
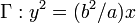. Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
;
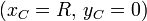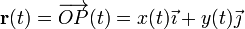, del punto P, así como sus vectores velocidad, 
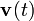, y aceleración, 
.
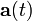