De Laplace

Contenido

1 Problemas de boletín
2 Problemas adicionales
- 2.1 Termómetro de gas con resorte
- 2.2 Variación de la densidad del agua
3 Preguntas de test

1 Problemas de boletín

1.1 Conversión entre escalas de temperaturas

Exprese las siguientes temperaturas en la escala Celsius, absoluta y Fahrenheit:

Cero absoluto
0°F
100°F
Punto triple del agua
Punto de fusión del azufre a 1 atm
Punto de sublimación del hielo seco a 1 atm

1.2 Dilatación de una esfera metálica

Se tiene una bola hueca de hierro que a 20°C tiene un radio interior de 12.0 mm y un radio exterior de 15.0 mm, siendo la densidad del hierro a esta temperatura 7874 kg/m³ y su coeficiente de dilatación lineal 11.8×10⁻⁶K⁻¹.

Se eleva la temperatura de la bola a 50°C. Determine:

Los nuevos radios interior y exterior de la bola.
La densidad del hierro a 50°C.
El incremento en el volumen ocupado por el hierro.
Si la bola de hierro está llena de aire que inicialmente tiene una presión de 100 kPa, ¿cuál será la presión del gas cuando la esfera está a 50°C?

1.3 Análisis de termómetro de mercurio

Se construye un termómetro empleando un capilar de 0.4 mm de diámetro en el que hay una columna de mercurio que a 0°C mide 2.0 cm. Suponiendo que el coeficiente de dilatación lineal vale 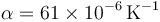$\alpha=61\times 10^{-6}\,\mathrm{K}^{-1}$ en el intervalo (0°C,100°C) y despreciando la dilatación del vidrio, ¿cuánto mediría la columna a 100°C si el mercurio fuera sólido? ¿Cuánto mide, teniendo en cuenta que es líquido? ¿Es esto suficiente para hacerlo legible?

Suponga ahora que en el extremo inferior del capilar hay una pequeña esfera que contiene 0.5 cm³ de mercurio, ¿cuánto medirá en ese caso la columna de mercurio a 100°C?

1.4 Compresión isoterma de un gas

Un cilindro vertical de sección cuadrada (esto es, un prisma) de 4.0 cm de lado contiene hidrógeno a 27°C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura. Se coloca sobre la tapa una pesa de 4.0 kg. Halle la altura de la tapa una vez que se alcanza de nuevo el equilibrio térmico con el exterior. ¿A qué temperatura habrá que calentar el gas para que la tapa vuelva a su posición inicial, con el peso todavía encima? (tómese 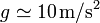$g\simeq 10\,\mathrm{m}/\mathrm{s}^2$ )

1.5 Variación de la presión de los neumáticos

Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la temperatura exterior es de 5°C. Si no los toca en seis meses y no hay fugas, ¿cuál será la presión manométrica un día de julio a 40°C? ¿Qué proporción de aire debe extraer de cada neumático para devolver la presión a 2.4 bar? Si tras reducir la presión se despreocupa otros seis meses, ¿cuál será la presión manométrica cuando vuelva a hacer 5°C? Desprecie la dilatación de los neumáticos.

1.6 Tubo con dos cámaras de gas

Se tiene una cámara cilíndrica horizontal de 20 cm de diámetro y 60 cm de longitud de paredes rígidas. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente está fijado con pernos. En la cámara de la izquierda hay 4.0 g de H₂ gaseoso y en la de la derecha 4.0 g de N₂. Los dos gases y el ambiente que los rodea están a 25°C.

Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central.
Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas

1.7 Compresión lineal de un gas

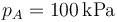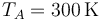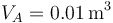Se comprime cuasiestáticamente un gas ideal que inicialmente se encuentra a presión $p_A = 100\,\mathrm{kPa}$ , temperatura $T_A = 300\,\mathrm{K}$ y ocupa un volumen $V_A = 0.01\,\mathrm{m}^3$ , según la ley

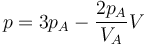
$p=3p_A-\frac{2p_A}{V_A}V$

La compresión continúa hasta que la presión vale $p B = 2 p A$ .

Calcule la temperatura final del gas. ¿Es este un proceso isotermo?
Trace la curva que describe el proceso en un diagrama pV.
¿Cuál es la temperatura máxima que alcanza el gas? ¿En qué estado la alcanza?

1.8 Termómetro de gas con líquido

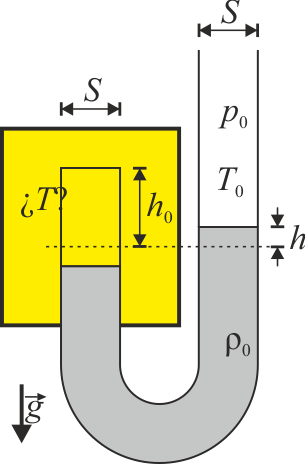
Se construye un termómetro de gas formado por un tubo de vidrio en U de sección $S$ , cerrado por uno de sus extremos. En el extremo que está cerrado se halla un gas ideal que cuando su presión es $p 0$ (la atmosférica) y su temperatura es $T 0$ (la del ambiente) ocupa una cámara de altura $h 0$ . El tubo contiene una cierta cantidad de líquido tal que a esta presión y temperatura los dos niveles están enrasados. El resto del tubo está abierto a la atmósfera.

Cuando el extremo cerrado se sumerge en un sistema cuya temperatura $T$ queremos determinar, se encuentra que el nivel del otro tubo se eleva a una altura $h$ sobre la de referencia.

¿Cuál es la temperatura del sistema?
Si en un proceso vemos que $h$ varía cuasiestáticamente desde $0$ a $h 1$ , ¿qué curva describe en un diagrama pV el gas ideal de la cámara?

2 Problemas adicionales

2.1 Termómetro de gas con resorte

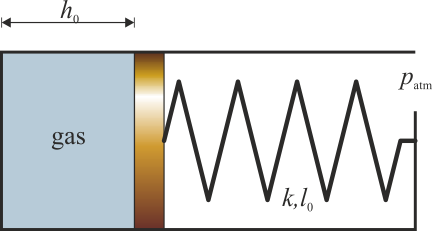
Se construye un termómetro de gas mediante un cilindro de sección $S$ en el interior del cual hay un pistón que puede deslizarse sin rozamiento. El pistón cierra una cámara en la que hay un gas ideal. La cara exterior del pistón está unida al extremo del tubo mediante un resorte de constante $k$ y longitud natural $l 0$ . Esta parte del tubo está abierta a la atmósfera. Para un cierto valor de la temperatura, $t 0$ , la presión es la atmosférica, el pistón se encuentra a una distancia $h 0$ del fondo y el resorte no ejerce fuerza alguna. Cuando el gas se calienta, se expande y el resorte se comprime.

Determine la temperatura del gas cuando el resorte se encuentra comprimido una distancia $x$ .
Indique cómo sería en un diagrama pV la curva correspondiente a un aumento cuasiestático de la temperatura entre $T 0$ y $T 1$ .

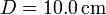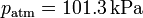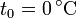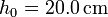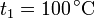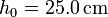Suponga que el diámetro del cilindro es $D=10.0\,\mathrm{cm}$ , la presión exterior $p_\mathrm{atm}=101.3\,\mathrm{kPa}$ , la altura del pistón a $t_0=0\,^\circ\mathrm{C}$ es $h_0=20.0\,\mathrm{cm}$ y a $t_1=100\,^\circ\mathrm{C}$ es $h_0=25.0\,\mathrm{cm}$ .

Calcule la constante del resorte.
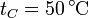
Determine la posición del pistón cuando $t_C=50\,^\circ\mathrm{C}$
Si queremos construir una escala para los grados Celsius con este termómetro, ¿estarán las líneas equiespaciadas?

2.2 Variación de la densidad del agua

La densidad del agua a 0°C vale 999.8395 kg/m³ a 4°C vale 999.9720 kg/m³ y a 10°C vale 999.7026 kg/m³. Determine aproximadamente el coeficiente de dilatación volumétrico a estas tres temperaturas.

3 Preguntas de test

3.1 Temperatura de un gas

Un gas ideal diatómico contenido en un recipiente ocupa un volumen de 500 cm³ a una presión de 4.0 bares y 300 K de temperatura. Experimenta una expansión hasta un estado final en el que ocupa un volumen de 1000 cm³ a una presión de 1.0 bares.

¿Cuál es la temperatura final del gas?

A 150 K
B Depende de si las paredes son adiabáticas o diatermas.
C 75 K
D 600 K

3.2 Temperatura en un proceso

Se tiene una cantidad fija de un gas ideal diatómico situada a una presión $p 0$ , volumen $V 0$ y temperatura $T 0$ . Experimenta un proceso tal que la presión final es $2 p 0$ y el volumen $2 V 0$ .

En este proceso, la temperatura…

A permanece constante.
B se reduce a la mitad.
C aumenta al doble.
D se multiplica por 4.

3.3 Número de psi en una atmósfera

Una atmósfera equivale a 101325 Pa. Un psi es la presión ejercida por una libra (4.448 N) sobre un cuadrado de lado 1 pulgada (2.54 cm). ¿A cuantos psi equivale una atmósfera?

A 1 atm = 579 psi
B 1 atm = 1.50 psi
C 1 atm = 6894 psi
D 1 atm = 14.7 psi

3.4 Título de una novela en Celsius

En el paso de grados Celsius a Fahrenheit se cumple 0°C = 32°F y 100°C = 212 °F. El título de la novela Fahrenheit 451 se refiere a la temperatura a la que arde el papel. ¿Cómo quedaría este título en la escala Celsius?

A Celsius 844
B Celsius 213
C Celsius 251
D Celsius 233

3.5 Densidad del aire húmedo

El aire seco (sin vapor de agua) equivale a un gas ideal de peso molecular 29 g/mol. El agua tiene peso molecular de 18 g/mol. El aire húmedo es el que tiene una cierta cantidad de vapor de agua. A 1 atm y 300 K, ¿qué aire es más denso, el seco o el húmedo?

A Los dos tienen la misma densidad.
B El seco.
C Depende de la humedad del aire.
D El húmedo.

3.6 Propiedad termométrica

Se tiene un sistema cerrado que contiene un gas ideal cuya temperatura puede cambiar. ¿Cuál de las siguientes propiedades no nos sirve para construir una escala para un termómetro?

A El número de moles.
B La energía interna.
C La presión.
D El volumen.

3.7 Dilatación de un paralelepípedo

El coeficiente de dilatación lineal del oro a 20 °C es 14×10⁻⁶°C⁻¹. Si se tiene un paralelepípedo de oro que a 20 °C ocupa 500 cm³, ¿cuánto aumenta el volumen cuando se calienta hasta 30 °C?

A 210 mm³
B 140 mm³
C 70 mm³
D 7 mm³

3.8 Volumen de gasolina

Una cierta cantidad de gasolina ocupa 1000 cm³ a 20 °C y 1019 cm³ a 40 °C. ¿Qué volumen ocupa a 80 °C?

A 1095 cm³
B 1057 cm³
C 1038 cm³
D 1076 cm³

3.9 Proceso en un gas

Un gas ideal diatómico ocupa un cierto volumen $V 0$ a una presión $p 0$ y una temperatura $T 0$ . Primero, manteniendo constante su volumen, se reduce lentamente su presión a $p 0 / 2$ . Luego, manteniendo constante su nueva presión, se pone gradualmente en contacto con un foco a temperatura $T 0$ . ¿Como se relacionan el volumen inicial, $V 0$ , y final $V f$ , del gas?

A $V f = V 0$
B $V f = V 0 / 2$
C $V f = 2 V 0$
D $V f = 4 V 0$

3.10 Dilatación de raíles

Los raíles ferroviarios son de acero y tienen 18 m de longitud a 20°C. Si deben operar entre -10°C y 60°, ¿qué espacio debe dejarse como mínimo entre un tramo y el siguiente si se tienden a una temperatura de 20°?

A 1 cm
B 2 cm
C 2 mm
D 5 mm

Dato: Coeficiente de dilatación lineal del acero: 13×10⁻⁶K⁻⁶

3.11 Dilatación de tapa

Una forma de abrir un bote de vidrio cuya tapa metálica está demasiado apretada consiste en sumergirlo en un baño de agua caliente. Si sumergimos en agua a 60 °C un bote de 4.0 cm de radio con tapa de estaño que a 20 °C encaja perfectamente y el coeficiente de dilatación lineal del vidrio es 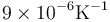$9\times 10^{-6}\mathrm{K}^{-1}$ y el del estaño es 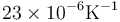$23\times 10^{-6}\mathrm{K}^{-1}$ , ¿cuánta holgura queda al calentarlo?

A 22 μm
B 560 μm
C 37 μm
D 920 μm

3.12 Escala de temperaturas basada en el metano

Zorg, un habitante de Titán, construye una escala de temperaturas basada en el metano tal que a la fusión (91 K) le corresponden 0 °Z y a la ebullición (116 K) 100 °Z. ¿Cuál es la temperatura del cero absoluto en esta escala?

A −187 °Z
B −364 °Z
C −91 °Z
D −25 °Z

Problemas de introducción a la termodinámica (GIE)