Variación de la densidad del agua

De Laplace

Contenido 1 Enunciado 2 Solución 3 Coeficiente a 0°C 4 Coeficiente a 10°C 5 Coeficiente a 4°C 6 Ajuste parabólico

1 Enunciado

La densidad del agua a 0°C vale 999.8395 kg/m³ a 4°C vale 999.9720 kg/m³ y a 10°C vale 999.7026 kg/m\³. Determine aproximadamente el coeficiente de dilatación volumétrico a estas tres temperaturas.

2 Solución

A partir de la densidad como función de la temperatura puede calcularse el coeficiente de dilatación volumétrico según la fórmula

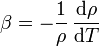
Si en vez de la densidad como función conocida de la temperatura, solo conocemos su valor en dos temperaturas próximas, podemos aproximar esta expresión mediante el cociente entre incrementos

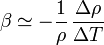
3 Coeficiente a 0°C

Entonces, si queremos hallar el valor aproximado del coeficiente de dilatación a 0°C podemos hacer uso de que conocemos la densidad en esa temperatura y a 4°C y hallar

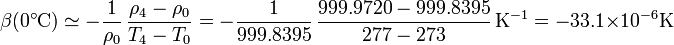
Para la densidad que aparece en el denominador podemos usar el valor a 0°C, el valor a 4°C o su media, ya que al ser la diferencia entre los valores, no se nota cambio apreciable en el resultado.

4 Coeficiente a 10°C

Para 10°C podemos operar de forma parecida considerando el incremento por la izquierda, esto es, desde 4°C a 10°C. Nos queda entonces

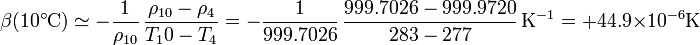
5 Coeficiente a 4°C

El problema surge cuando queremos hallar el coeficiente de dilatación a 4°C. ¿Tomamos el incremento por la izquierda, en cuyo caso nos daría el primer resultado, negativo, o el de la derecha y nos resultaría el segundo valor, positivo? ¿Es negativo o positivo el coeficiente de dilatación a 4°C?

La causa del problema es el extraño comportamiento del agua. Para cualquier sustancia, el coeficiente de dilatación suele ser una función siempre creciente, β > 0 por lo que da igual que lo calculemos con los incrementos por la derecha o por la izquierda.

Debido a la anomalía térmica del agua, la densidad es máxima a 4°C. Esto quiere decir que en este punto la derivada respecto a la temperatura es nula (como corresponde a un extremo) y por tanto, también lo será el coeficiente de dilatación

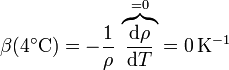
6 Ajuste parabólico

Podemos hacer un cálculo numérico más preciso empleando simultáneamente los tres datos que tenemos. Cuando hacemos un cociente entre incrementos estamos hallando una pendiente de una recta, es decir, dados dos puntos en la gráfica, se halla la recta que pasa por esos dos puntos y se calcula su pendiente. Se trata de una aproximación lineal. Este método falla bastante en las proximidades de un extremo.

Podemos mejorar la aproximación si en lugar de una recta (una curva de primer grado) usamos una parábola (una curva de segundo grado). Suponemos una función de la temperatura de coeficientes desconocidos tal que

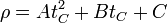
y aplicamos que sabemos que pasa por los tres puntos que conocemos

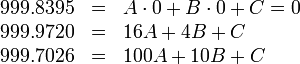
Esto es un sistema de tres ecuaciones con tres incógnitas, con solución en el SI

Ahora, una vez que tenemos esta función aproximada, podemos hallar el coeficiente a las tres temperaturas empleando la fórmula original

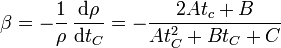
y obtenemos a 0°C

a 4°C

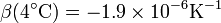
y a 10°C

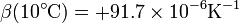
Vemos que el resultado con este método perfeccionado se aleja bastante del calculado con la aproximación de tramos rectos.