Termómetro de gas con resorte

De Laplace

Contenido

1 Enunciado
2 Temperatura del gas
3 Curva en el diagrama pV
4 Constante del resorte
5 Posición a 50°C
6 Escala de temperaturas

1 Enunciado

Se construye un termómetro de gas mediante un cilindro de sección $S$ en el interior del cual hay un pistón que puede deslizarse sin rozamiento. El pistón cierra una cámara en la que hay un gas ideal. La cara exterior del pistón está unida al extremo del tubo mediante un resorte de constante $k$ y longitud natural $l 0$ . Esta parte del tubo está abierta a la atmósfera. Para un cierto valor de la temperatura, $t 0$ , la presión es la atmosférica, el pistón se encuentra a una distancia $h 0$ del fondo y el resorte no ejerce fuerza alguna. Cuando el gas se calienta, se expande y el resorte se comprime.

Determine la temperatura del gas cuando el resorte se encuentra comprimido una distancia $x$ .
Indique cómo sería en un diagrama pV la curva correspondiente a un aumento cuasiestático de la temperatura entre $T 0$ y $T 1$ .

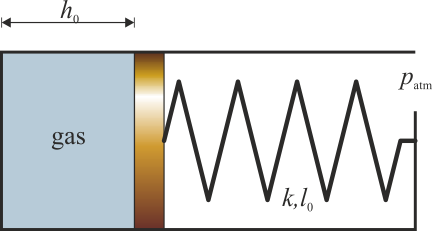
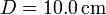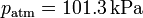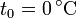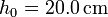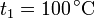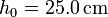Suponga que el diámetro del cilindro es $D=10.0\,\mathrm{cm}$ , la presión exterior $p_\mathrm{atm}=101.3\,\mathrm{kPa}$ , la altura del pistón a $t_0=0\,^\circ\mathrm{C}$ es $h_0=20.0\,\mathrm{cm}$ y a $t_1=100\,^\circ\mathrm{C}$ es $h_0=25.0\,\mathrm{cm}$ .

Calcule la constante del resorte.
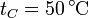
Determine la posición del pistón cuando $t_C=50\,^\circ\mathrm{C}$
Si queremos construir una escala para los grados Celsius con este termómetro, ¿estarán las líneas equiespaciadas?

2 Temperatura del gas

Cuando el gas se expande debe vencer no solo la presión del aire exterior (la atmosférica), sino también la fuerza recuperadora del resorte. Esto hace que en este proceso no se mantenga constante ni la presión, ni el volumen ni la temperatura.

De acuerdo con la ley de los gases ideales, para una cantidad dada de gas, se cumple la igualdad entre dos estados

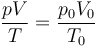
$\frac{pV}{T}=\frac{p_0V_0}{T_0}$

En este caso tomaremos como estado “0” el correspondiente a $t 0$ , en el que el muelle tiene su longitud natural (no ejerce fuerza sobre el gas), la presión es la atmosférica y el volumen es el inicial e igual a $S h 0$ .

Cuando el gas se expande, la distancia del pistón al fondo pasa a ser

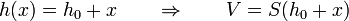
$h(x) = h_0+x\qquad\Rightarrow\qquad V = S(h_0+x)$

mientras que la presión iguala a la exterior, suma de la atmosférica y de la debida al muelle

$p = p_0+\frac{kx}{S}$

Llevando esto a la ecuación de los gases ideales resulta la igualdad

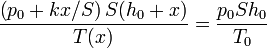
$\frac{\left(p_0+kx/S\right)S(h_0+x)}{T(x)} = \frac{p_0Sh_0}{T_0}$

que nos permite despejar la temperatura como función de la posición del émbolo

$T(x) = T_0\frac{\left(p_0+kx/S\right)(h_0+x)}{p_0h_0}$

Esta es una función de segundo grado cuya gráfica nos da una parábola.

3 Curva en el diagrama pV

Para obtener la curva no necesitamos despejar $x$ como función de la temperatura, ya que solo precisamos la relación entre la presión $p$ y el volumen $V$ . Podemos poner ambas variables en función de la posición del émbolo

$p = p_0+\frac{k}{S}x\qquad\qquad V = Sh_0+Sx$

que nos dice la curva en el diagrama pV es una recta de pendiente positiva. Si queremos, podemos eliminar x en las ecuaciones

$x = \frac{V}{S}-h_0\qquad\Rightarrow\qquad p = \left(p_0 -\frac{kh_0}{S}\right)+ \frac{k}{S^2}V$

En la gráfica vemos la recta superpuesta a una serie de hipérbolas que serían las diferentes isotermas del gas. Los datos numéricos de esta gráfica corresponden a los valores calculados en los apartados siguientes.

4 Constante del resorte

Si nos dan dos datos de la posición ( $x 0 = 0$ y un valor $x 1$ conocido), podemos emplearlo para determinar la constante del resorte. Partimos de la igualdad que obtuvimos antes

$T(x) = T_0\frac{\left(p_0+kx/S\right)(h_0+x)}{p_0h_0}$

de la que se puede despejar la presión

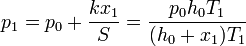
$p_1=p_0+\frac{kx_1}{S} = \frac{p_0h_0T_1}{(h_0+x_1)T_1}$

y de aquí la constante del muelle

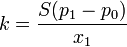
$k = \frac{S(p_1-p_0)}{x_1}$

Sustituyendo los valores numéricos nos queda la presión a 100°C

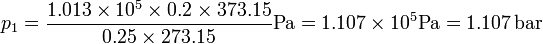
$p_1= \frac{1.013\times 10^5\times 0.2\times 373.15}{0.25\times 273.15} \mathrm{Pa} = 1.107\times 10^5\mathrm{Pa} = 1.107\,\mathrm{bar}$

y la constante del muelle

$k = \frac{\pi 0.05^2}{0.05}((1.107-1.013)\times 10^5\,\frac{\mathrm{N}}{\mathrm{m}} = 1.48\,\frac{\mathrm{kN}}{\mathrm{m}}$

5 Posición a 50°C

Una vez que tenemos el valor de la constante, ya podemos dar una expresión numérica para la temperatura como función de la posición. Si medimos el desplzamiento del émbolo en centímetros queda

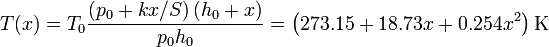
$T(x) = T_0\frac{\left(p_0+kx/S\right)(h_0+x)}{p_0h_0} = \left(273.15 + 18.73 x +0.254 x^2\right)\mathrm{K}$

y pasando a grados Celsius

$t_C(x) = \left(18.73 x +0.254 x^2\right)^\circ\mathrm{C}$

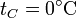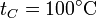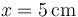En el intervalo (0°C,100°C) esta curva es un arco de parábola que pasa por $t_C = 0^\circ\mathrm{C}$ en $x = 0$ y por $t_C=100^\circ\mathrm{C}$ en $x = 5\,\mathrm{cm}$ .

El valor de la posición para 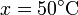$x = 50^\circ\mathrm{C}$ lo calculamos resolviendo la ecuación de segundo grado

$18.73x+0.254x^2 = 50\qquad\Rightarrow\qquad x = 2.58\,\mathrm{cm}$

(existe otra solución, pero es absurda, pues da una posición negativa).

6 Escala de temperaturas

De que la curva T(x) sea una parábola se deduce que la escala no puede ser lineal y las marcas no estarán equiespaciadas. Para que salga una escala uniforme la variación en la posición debe ser proporcional a la variación en temperaturas. Esto implicaría que a 50°C la marca debería estar en el punto medio entre la de 0°C y la de 100°C. Sin embargo, tal como se ve en el apartado anterior, no se encuentra en 2.50cm, sino un poco más allá.

Gráficamente se ve en que la curva de la posición frente a la temperatura no pasa por los nodos de la rejilla. Vemos, no obstante, que la diferencia con una escala lineal (que sería una recta) es muy pequeña.

Termómetro de gas con resorte

De Laplace

Contenido

1 Enunciado

2 Temperatura del gas

3 Curva en el diagrama pV

4 Constante del resorte

5 Posición a 50°C

6 Escala de temperaturas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES