Termómetro de gas con líquido

De Laplace

1 Enunciado

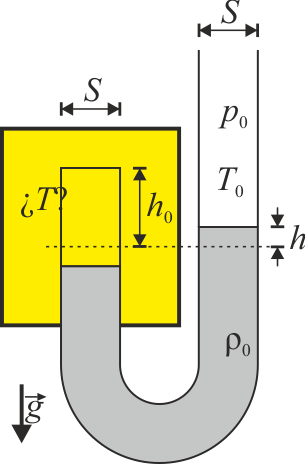
Se construye un termómetro de gas formado por un tubo de vidrio en U de sección S, cerrado por uno de sus extremos. En el extremo que está cerrado se halla un gas ideal que cuando su presión es p₀ (la atmosférica) y su temperatura es T₀ (la del ambiente) ocupa una cámara de altura h₀. El tubo contiene una cierta cantidad de líquido tal que a esta presión y temperatura los dos niveles están enrasados. El resto del tubo está abierto a la atmósfera.

Cuando el extremo cerrado se sumerge en un sistema cuya temperatura T queremos determinar, se encuentra que el nivel del otro tubo se eleva a una altura h sobre la de referencia.

1. ¿Cuál es la temperatura del sistema?
2. Si en un proceso vemos que h varía cuasiestáticamente desde 0 a h₁, ¿qué curva describe en un diagrama pV el gas ideal de la cámara?

2 Cálculo de la temperatura

Por la ley de los gases ideales para el gas contenido en la cámara

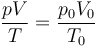
de donde la temperatura es igual a

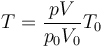
Necesitamos entonces hallar el nuevo volumen y la nueva presión del gas.

Cuando el nivel sube una altura h en el tubo abierto, baja la misma altura en el cerrado (por ser de la misma sección). Por tanto, el nuevo volumen es

La presión la da la hidrostática. Puesto que hay un desnivel 2h respecto al brazo abierto, la presión será la armosférica más la correspondiente a este desnivel

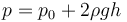
Llevando esto a la expresión de la temperatura

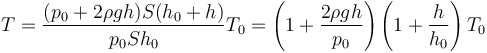
Vemos que no resulta una escala lineal de temperaturas, sino que la temperatura aumenta parabólicamente con la altura. O lo que es lo mismo, la altura con que medimos la temperatura varía como una función que incluye raíces cuadradas.

3 Representación en un diagrama pV

Caundo se va modificando la temperatura, va cambiando la elevación según las pexresiones que hemos ya indicado

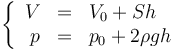
Empleando h como variable, estas son las ecuaciones paramétricas de una recta de pendiente positiva. Por tanto, sobre un diagrama pV el proceso se representará como un segmento inclinado.