Análisis de termómetro de mercurio

De Laplace

Contenido

1 Enunciado
2 Dilatación como sólido
3 Dilatación como líquido
4 Efecto del depósito

1 Enunciado

Se construye un termómetro empleando un capilar de 0.4 mm de diámetro en el que hay una columna de mercurio que a 0°C mide 2.0 cm. Suponiendo que el coeficiente de dilatación lineal vale 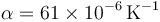$\alpha=61\times 10^{-6}\,\mathrm{K}^{-1}$ en el intervalo (0°C,100°C) y despreciando la dilatación del vidrio, ¿cuánto mediría la columna a 100°C si el mercurio fuera sólido? ¿Cuánto mide, teniendo en cuenta que es líquido? ¿Es esto suficiente para hacerlo legible?

Suponga ahora que en el extremo inferior del capilar hay una pequeña esfera que contiene 0.5 cm³ de mercurio, ¿cuánto medirá en ese caso la columna de mercurio a 100°C?

2 Dilatación como sólido

Si el mercurio fuera un sólido, tendríamos una dilatación lineal de la barra, de forma que su longitud para cada temperatura vale

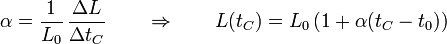
$\alpha = \frac{1}{L_0}\,\frac{\Delta L}{\Delta t_C}\qquad\Rightarrow\qquad L(t_C)=L_0\left(1+\alpha(t_C-t_0)\right)\,$

En este caso, esto nos daría un incremento relativo

$\frac{\Delta L}{L_0}=\alpha\,\Delta t_C = 61\times 10^{-6}\times 100 = 0.61\%$

es decir, de menos del 1%. Esto supondría una dilatación

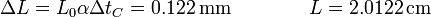
$\Delta L = L_0\alpha\Delta t_C = 0.122\,\mathrm{mm}\qquad\qquad L = 2.0122\,\mathrm{cm}$

Se dilata un poco más de una décima de milímetro, lo que es claramente inobservable en un termómetro.

3 Dilatación como líquido

El cálculo anterior no es válido porque no tiene en cuenta que el mercurio es un líquido. Debemos tener en cuenta el aumento de volumen, no de longitud, ya que al aumentar en volumen y poder fluir el resultado es que el líquido “trepa” por el tubo, aumentando el nivel más lo que subiría un sólido.

El coeficiente de dilatación volumétrica para el mercurio vale

$\beta = 3\alpha = 1.83\times 10^{-4}\,\mathrm{K}^{-1}$

Lo que nos da un aumento relativo del volumen

$\frac{\Delta V}{V_0}=\beta\,\Delta t_C = 1.83\%$

Este incremento del volumen se va todo en subir el nivel, ya que si despreciamos la dilatación del vidrio, la sección no cambia

$V = SL\qquad\Rightarrow\qquad \Delta V = S\,\Delta L$

lo que nos da un incremento relativo de la altura

$\frac{\Delta L}{L}=\frac{\Delta V}{V} = 1.83\%$

es decir, la altura crece en algo menos del 2%, lo que sigue siendo una cantidad ridícula si queremos medir 100 grados con ella

$\Delta L = 0.0183\times 2\,\mathrm{cm} = 0.0366\,\mathrm{cm}\qquad\Rightarrow\qquad L = 2.0366\,\mathrm{cm}$

4 Efecto del depósito

Para poder incrementar la subida del nivel y hacerlo legible se recurre a la inclusión de un depósito en el extremo del tubo. En este caso, lo que sube por el capilar es lo debido a la expansión de todo el mercurio, incluyendo el del depósito.

La expansión relativa del volumen es la misma que antes

$\frac{\Delta V}{V_0}=\beta\,\Delta t_C=1.83\%$

pero ahora se trata del 1.83% de un volumen mucho mayor

$V_0 = V_\mathrm{dep}+SL_0\qquad\qquad \Delta V = S\,\Delta L$

lo que nos da

$\Delta L = \left(L_0+\frac{V_\mathrm{dep}}{S}\right)\beta \,\Delta t_C$

Sustituyendo los valores del enunciado

$\Delta L = \left(2.0\,\mathrm{cm}+\frac{0.5\mathrm{cm}^3}{\pi(0.02\,\mathrm{cm})^2}\right)\times 0.0183 = 7.32\,\mathrm{cm}$

que ya sí es bastante legible (aunque los grados individuales en la escala estarían separados menos de un milímetro).

Análisis de termómetro de mercurio

De Laplace

Contenido

1 Enunciado

2 Dilatación como sólido

3 Dilatación como líquido

4 Efecto del depósito

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES