Problemas de introducción a la mecánica de fluidos

De Laplace

1 Masa y altura media de la atmósfera

Si el radio de la Tierra es 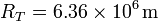y la presión atmosférica a nivel del mar es 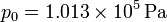, calcule la masa total de la atmósfera, suponiendo que todos sus puntos están sometidos al mismo valor de 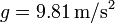. Si la densidad de masa de la atmósfera fuese la del aire a nivel del mar, 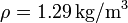, calcule la altura de la atmósfera sobre la superficie de la Tierra.

Solución

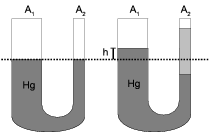
2 Elevación de mercurio en un tubo en U

Se vierte mercurio en un un tubo en U. El brazo izquierdo del tubo tiene una sección transversal de área A₁ = 10.0 cm², y la del brazo derecho es A₂ = 5.00 cm². A continuación se vierten 100 g de agua en el brazo derecho del tubo.

1. Determina la altura de la columna de agua en el brazo derecho del tubo relativa a la del mercurio en el izquierdo.
2. Si la densidad del mercurio es ρ_Hg = 13.6 g/cm³, ¿qué distancia ascenderá el mercurio en el brazo izquierdo?

Solución

3 Presión en el interior del océano

Calcule la presión absoluta a 1000 m de profundidad en el océano. Considere que la densidad del agua es 1024 kg/m³ y que el aire que hay encima ejerce una presión de 101.3 kPa. A esta profundidad, ¿qué fuerza debe ejercer el armazón de la escotilla circular, de radio 30.0 cm, de un submarino para contrarrestar la fuerza del agua?

Solución

4 Modelo de atmósfera isoterma

Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión, demuestre que la variación de la presión atmosférica con la altura es P(y) = P₀e ^{− αy}, siendo g la aceleración de la gravedad y α = ρ₀g / P₀, con ρ₀ y P₀ la densidad del aire y la presión atmosférica a nivel del mar (y = 0).

Solución

5 Modelo de densímetro

Un modelo sencillo de densímetro consiste en una jeringuilla en cuyo interior hay una barra delgada de longitud L y densidad de masa ρ₀ conocida. Se aspira dentro de la jeringuilla una cantidad del líquido del que se quiere medir la densidad ρ, de modo que la barra flota parcialmente en él, sobresaliendo una distancia h. Encuentre la expresión que da la densidad del líquido.

Solución

6 Oscilaciones de un cuerpo parcialmente sumergido

Una barra cilíndrica muy larga de radio r tiene uno de sus extremos más pesado, de modo que flota en posición vertical cuando se sumerge en un líquido de densidad de masa ρ. El extremo superior sobresale de la superficie del líquido en el aire, sometido a una presión p₀. Se empuja la barra hacia abajo una distancia d respecto de su posición de equilibrio. Demuestra que la barra describirá un movimiento armónico simple si se desprecia la resistencia ofrecida por el líquido, y calcula el periodo de oscilación.

Solución

7 Perfil parabólico de velocidades

Tenemos un flujo que circula por una tubería de sección rectangular, con lados a y b y longitud L. Si 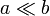, se puede considerar que la tubería está formada por dos planos paralelos separados por una distancia a e infinitos en la dirección transversal al flujo. Se impone una diferencia de presión Δp entre los extremos de la tubería. Debido a la viscosidad, las capas de fluido en contacto con las paredes no se mueven y el perfil de velocidades es parabólico de la forma

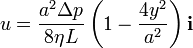
La coordenada y se escoge de modo que los planos están en .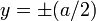

1. Determina la fuerza tangencial por unidad de superficie que el líquido ejerce sobre las placas.
2. Calcula el flujo de masa a través de la sección de la tubería.

Solución

8 Tubo de Venturi

El tubo de Venturi se utiliza para medir la velocidad de un fluido incompresible. Consiste en un tubo con un estrechamiento, de modo que las secciones antes y después del estrechamiento son A₁ y A₂, con A₁ > A₂. En cada parte del tubo hay un manómetro, de modo que se pueden medir las presiones respectivas p₁ y p₂. Encuentra una expresión para la velocidad del fluido en cada parte del tubo en función del área de las secciones, las presiones y su densidad.

Solución

9 Velocidad de salida de un depósito

Un tanque cerrado contiene un líquido de densidad ρ, y tiene un orificio lateral a una distancia y₁ del fondo. El diámetro del orificio es pequeño en comparación con el diámetro del tanque. El aire del interior del tanque que está encima del líquido se encuentra a una presión p. Considera que se trata de un flujo laminar sin fricción.

1. Demuestra que la velocidad a la que el fluido sale por el orificio cuando la superficie del líquido está a una altura h respecto a él es

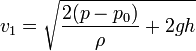
2. Considera el caso p = p₀. Calcula la distancia a la que llega el agua que sale del orificio en función de y₂ y h. Supongamos que podemos variar la altura del orificio. Para un valor fijo de y₂, ¿qué valor de h hace máxima la distancia que alcanza el chorro?

Solución

10 Vaciado de un depósito cilíndrico

Se tiene un recipiente cilíndrico de radio R y altura H abierto a la atmósfera, que se llena hasta una altura h = H / 2 de mercurio. Entonces, se cierra herméticamente por su parte superior, quedando una cámara de aire entre el mercurio y la tapa. En la parte inferior del recipiente se abre un pequeño orificio de radio a.

1. Suponiendo que el aire dentro del recipiente se comporta como un gas ideal y que su temperatura permanece constante, encuentra la presión del aire cuando el mercurio llega hasta una altura z.
2. Halla la expresión que da la velocidad con la que sale el mercurio cuando el nivel superior del mercurio está a una altura z
3. ¿Puede vaciarse completamente el recipiente? Si no es así, encuentra la ecuación que da la altura final del mercurio en el recipiente.
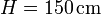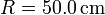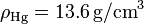4. Supón que , , y . Calcula el valor numérico del apartado anterior y la cantidad de mercurio que ha salido del recipiente.

Solución

11 Diseño de una clepsidra

Una clepsidra es un reloj de agua, usado en tiempos antiguos para medir el tiempo. Un modelo simple consiste en un recipiente abierto al aire en su parte superior, con un agujero de pequeña sección en el fondo. El recipiente se llena de agua y esta fluye por el agujero. La variación del nivel de agua en el recipiente indica el paso del tiempo. Para poder usar una escala equiespaciada es conveniente que la velocidad con que baja el nivel de agua sea constante. Si la forma del recipiente es de un volumen de revolución, de modo que para cada altura su sección es un círculo de radio r(y), y el radio del orificio de salida es r₀, encuentra el perfil de la curva que consigue que la velocidad con que desciende el nivel de agua sea constante.

Solución