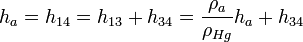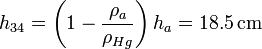Elevación de mercurio en un tubo en U

De Laplace

1 Enunciado

Se vierte mercurio en un un tubo en U. El brazo izquierdo del tubo tiene una sección transversal de área $A 1 = 10.0$ cm², y la del brazo derecho es $A 2 = 5.00$ cm². A continuación se vierten 100 g de agua en el brazo derecho del tubo.

Determina la altura de la columna de agua en el brazo derecho del tubo relativa a la del mercurio en el izquierdo.
Si la densidad del mercurio es $ρ H g = 13.6$ g/cm³, ¿qué distancia ascenderá el mercurio en el brazo izquierdo?

2 Solución

Sabiendo que la densidad del agua es 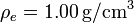$\rho_e = 1.00\,\mathrm{g/cm^3}$ , la altura de la columna de agua puede calcularse en función de su masa y la sección del tubo de la derecha

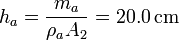
$m a = ρ a V a = ρ a A 2 h a$ $\Rightarrow$ $h_a = \frac{m_a}{\rho_aA_2} = 20.0\,\mathrm{cm}$

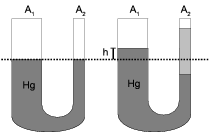
Numeramos los niveles de la figura, de modo que el nivel 1 corresponde a la altura del mercurio en el tubo de la derecha, el nivel 2 es la altura original del mercurio antes de añadir el agua, el 3 corresponde a la altura del mercurio en el tubo de la izquierda y el 4 es la superficie libre de la superficie de agua en el tubo de la derecha.

En ambas superficies libres, la del mercurio a la izquierda (nivel 3) y la de agua a la derecha (nivel 4) la presión ejercida sobre ellas es la atmosférica, $P 0$ . El principio de Pascal implica que los puntos de un mismo líquido a la misma altura respecto a la gravedad están a la misma presión. Podemos aplicar este principio al nivel 1. En el tubo de la izquierda la presión se debe a la presión atmosférica y la columna de mercurio desde la superficie libre hasta la altura 1. En el tubo de la derecha la presión es la suma de la presión atmosférica y la ejercida por la columna completa de agua. Así

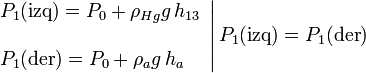
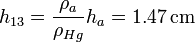
$\left. \begin{array}{l} P_1(\mathrm{izq}) = P_0 + \rho_{Hg}g\,h_{13} \\ \\ P_1(\mathrm{der}) = P_0 + \rho_a g\,h_a \end{array} \right| P_1(\mathrm{izq}) = P_1(\mathrm{der})$ $\Rightarrow$ $h_{13} = \frac{\rho_a}{\rho_{Hg}}h_a = 1.47\,\mathrm{cm}$

Por otro lado, el aumento de nivel de mercurio en la izquierda, $h = h 23$ , se debe al trasvase de volumen de mercurio desde el tubo derecho. Como el líquido es incompresible el volumen se conserva, y entonces

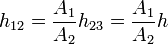
$A 1 h 23 = A 2 h 12$ $\Rightarrow$ $h_{12} = \frac{A_1}{A_2}h_{23}= \frac{A_1}{A_2}h$

Ahora bien, si observamos la figura vemos que

$h 13 = h 12 + h 23 = h 12 + h$

Sustituyendo las expresiones anteriores tenemos

$\frac{\rho_a}{\rho_{Hg}}h_a = \frac{A_1}{A_2}h + h$ $\Rightarrow$ $h = h_{23} = \frac{\displaystyle\frac{\rho_a}{\rho_{Hg}}}{\displaystyle 1+\frac{A_1}{A_2}}h_a = 0.490\,\mathrm{cm}$

Ahora podemos calcular la diferencia de alturas entre las superficies libres de ambos tubos. Tenemos

$h_a = h_{14} = h_{13} + h_{34} = \frac{\rho_a}{\rho_{Hg}}h_a + h_{34}$ $\Rightarrow$ $h_{34} = \left(1-\frac{\rho_a}{\rho_{Hg}}\right)h_a = 18.5\,\mathrm{cm}$

Elevación de mercurio en un tubo en U

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES