Perfil parabólico de velocidades

De Laplace

1 Enunciado

Tenemos un fluido que circula por una tubería de sección rectangular, con lados $a$ y $b$ y longitud $L$ . Si 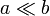$a\ll b$ , se puede considerar que la tubería está formada por dos planos paralelos separados por una distancia $a$ e infinitos en la dirección transversal al flujo. Se impone una diferencia de presión $Δ p$ entre los extremos de la tubería. Debido a la viscosidad, las capas de fluido en contacto con las paredes no se mueven y el perfil de velocidades es parabólico de la forma

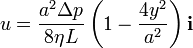
$u = \frac{a^2\Delta p}{8\eta L}\left(1-\frac{4y^2}{a^2}\right)\mathbf{i}$

La coordenada $y$ se escoge de modo que los planos están en 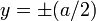$y = \pm(a/2)$ .

Determina la fuerza tangencial por unidad de superficie que el líquido ejerce sobre las placas.
Calcula el flujo de masa a través de la sección de la tubería.

2 Fuerza tangencial sobre las placas

La propiedad definitoria de los fluidos es su comportamiento frente a una fuerza de cizalla (una tangencial a su superficie). Mientras que un sólido se deforma en la dirección de la fuerza, un fluido adquiere una velocidad en dicha dirección. No obstante, debido al rozamiento entre las distintas capas del fluido provoca que no todo él adquiera la misma velocidad, sino que adquiere un perfil de velocidades no uniforme.

El caso más sencillo (conocido como perfil de Couette) es el de un líquido comprendido entre dos láminas paralelas, una de las cuales está fija, mientras la otra se mueve, arrastrando el líquido con ella. Si 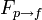$F_{p\to f}$ es la magnitud de la fuerza de cizalla aplicada por la pared superior sobre el fluido, $u$ es la componente de la velocidad en la dirección de esta fuerza e $y$ es la coordenada perpendicular a la superficie (y a la fuerza) dirigida hacia el exterior del fluido, la relación entre la cizalla por unidad de superficie y el gradiente de velocidades es

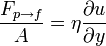
$\frac{F_{p\to f}}{A} = \eta \frac{\partial u}{\partial y}$

siendo $η$ la viscosidad.

De acuerdo con la tercera ley de Newton, si en el fluido aparece un gradiente en las velocidades, ejercerá una fuerza sobre las paredes igual a

$F_{f\to p} = -A\eta \frac{\partial u}{\partial y}$

En el caso del líquido entre la lámina fija y la móvil, tirará de la inferior hacia adelante, y de la superior hacia atrás.

En el caso de que trata este problema tenemos un líquido entre dos láminas paralelas, que forman una tubería plana (un canal). Sobre el líquido en la tubería se ha aplicado una diferencia de presiones que lo pone en movimiento. El rozamiento con las paredes impone que justo sobre ellas la velocidad es nula, lo que produce el denominado perfil parabólico de velocidades (o de Poiseuille) con un máximo en el plano central y valor nulo sobre las paredes.

Los gradientes junto a las paredes producen fuerzas sobre estas, tendiendo a arrastrarlas en su movimiento.

La fuerza sobre la cara superior, situada en $y = + a / 2$ es

$\mathbf{F}_1 = -A\eta \frac{\partial u}{\partial y}\mathbf{i}=-(bL)\eta \left(\frac{a^2\Delta p}{8\eta L}\right)\left(\frac{-8y}{a^2}\right)_{a/2}\mathbf{i}=\frac{ab\,\Delta p}{2} \mathbf{i}$

Podemos ver que el resultado final tiene dimensiones de presión por área, una fuerza, como debe de ser.

Por la simetría del sistema, la misma fuerza se ejerce sobre la cara inferior, pero en este caso, hay que tener cuidad que la dirección hacia el exterior la dan los valores decrecientes de y, por lo que hay que cambiar el signo de la derivada.

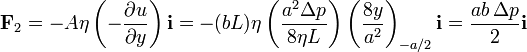
$\mathbf{F}_2 = -A\eta\left(-\frac{\partial u}{\partial y}\right)\mathbf{i}=-(bL)\eta \left(\frac{a^2\Delta p}{8\eta L}\right)\left(\frac{8y}{a^2}\right)_{-a/2}\mathbf{i}=\frac{ab\,\Delta p}{2} \mathbf{i}$

3 Flujo másico

El flujo másico de un fluido, $Q m$ , a través de una cierta sección transversal $S$ viene dado por la integral de superficie

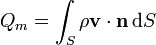
$Q_m = \int_S \rho\mathbf{v}\cdot\mathbf{n}\,\mathrm{d}S$

Si consideramos una sección transversal de la tubería el vector normal a esta sección es 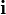$\mathbf{i}$ y el diferencial de superficie es

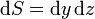
$\mathrm{d}S=\mathrm{d}y\,\mathrm{d}z$

y el cálculo del flujo se expresa

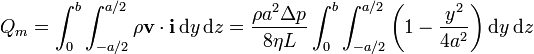
$Q_m = \int_0^b\int_{-a/2}^{a/2}\rho \mathbf{v}\cdot\mathbf{i}\,\mathrm{d}y\,\mathrm{d}z = \frac{\rho a^2\Delta p}{8\eta L}\int_0^b\int_{-a/2}^{a/2}\left(1-\frac{y^2}{4a^2}\right)\mathrm{d}y\,\mathrm{d}z$

El integrando no depende de $z$ , así que al integrar en esta coordenada simplemente obtenemos un factor $b$ . La integral en $y$ da

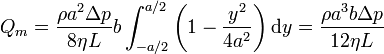
$Q_m = \frac{\rho a^2\Delta p}{8\eta L}b\int_{-a/2}^{a/2}\left(1-\frac{y^2}{4a^2}\right)\mathrm{d}y=\frac{\rho a^3b\Delta p}{12\eta L}$

Vemos que el flujo de masa (y de volumen) a través de la tubería es proporcional a la diferencia de presiones aplicadas. O, equivalentemente, la diferencia de presiones es proporcional al flujo

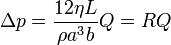
$\Delta p = \frac{12\eta L}{\rho a^3b}Q = RQ$

Este tipo de relaciones permite desarrollar un modelo del flujo a través de tuberías de una manera análoga al estudio de resistencias eléctricas (para las cuales la diferencia de potencial es proporcional a la intensidad de corriente, $Δ V = I R$ ).

Perfil parabólico de velocidades

De Laplace

1 Enunciado

2 Fuerza tangencial sobre las placas

3 Flujo másico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES