Masa y altura media de la atmósfera
De Laplace
1 Enunciado
Si el radio de la Tierra es 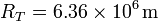 y la presión atmosférica a nivel del mar es
y la presión atmosférica a nivel del mar es 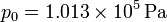 , calcule la masa total de la atmósfera, suponiendo que todos sus puntos están sometidos al mismo valor de
, calcule la masa total de la atmósfera, suponiendo que todos sus puntos están sometidos al mismo valor de 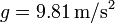 . Si la densidad de masa de la atmósfera fuese la del aire a nivel del mar,
. Si la densidad de masa de la atmósfera fuese la del aire a nivel del mar, 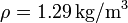 , calcule la altura de la atmósfera sobre la superficie de la Tierra.
, calcule la altura de la atmósfera sobre la superficie de la Tierra.
2 Solución
El modelo más simple de atmósfera es aquel que presupone que está formada por un fluido de densidad homogénea. Este modelo es demasiado elemental para el estudio de casi todos los fenómenos atmosféricos, pero para estimar la masa y el tamaño de la atmósfera es suficiente. Un modelo un poco más refinado es el denominado modelo de atmósfera isoterma.
Si la presión sobre un punto de la superficie es p0, esto quiere decir que sobre un elemento de superficie dA de la superficie terrestre se ejerce una fuerza
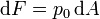
Esta fuerza es igual al peso de toda la columna de aire que se encuentra sobre el elemento. Si la densidad es la misma en todos los puntos
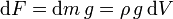
y el volumen de la columna es igual a la sección multiplicada por la altura media
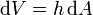
así que
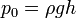

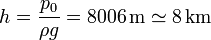
Esta distancia es mucho menor que el espesor real de la atmósfera (que se cifra en centenares de kilómetros), pero es una estimación adecuada del tamaño de la zona donde se concentra la mayor parte del aire, que es a ras de suelo.
Podemos hallar la masa de la atmósfera calculando la masa de una columna de aire que se apoya sobre un elemento de superficie dA y sumando para todo el área de la superficie terrestre
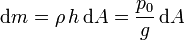
y resulta la masa total
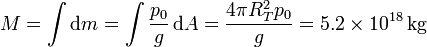
El valor estimado de la masa de la atmósfera se estima, a partir de cálculos más elaborados que tienen en cuenta la variación de la gravedad con la altura, en 5.14×1018 kg, con lo que vemos que hemos obtenido un resultado muy próximo al real. La razón de que este modelo tan simple de atmósfera homogénea de tan buen resultado es que realmente para hallar la masa sólo nos hace falta la presión atmosférica a nivel del mar y esa es independiente de cómo varía la densidad con la altura.
Dado que la masa total de la tierra es 5.9×1024 kg, vemos que la atmósfera supone menos de una millonésima de la masa total terrestre.





