Vaciado de un depósito cilíndrico

De Laplace

Contenido

1 Enunciado
2 Presión del aire
3 Velocidad de salida
4 Vaciado parcial
5 Valores numéricos
6 Solución refinada

1 Enunciado

Se tiene un recipiente cilíndrico de radio $R$ y altura $H$ abierto a la atmósfera, que se llena hasta una altura $h = H / 2$ de mercurio. Entonces, se cierra herméticamente por su parte superior, quedando una cámara de aire entre el mercurio y la tapa. En la parte inferior del recipiente se abre un pequeño orificio de radio $a$ .

Suponiendo que el aire dentro del recipiente se comporta como un gas ideal y que su temperatura permanece constante, encuentra la presión del aire cuando el mercurio llega hasta una altura $z$ .
Halla la expresión que da la velocidad con la que sale el mercurio cuando el nivel superior del mercurio está a una altura $z$
¿Puede vaciarse completamente el recipiente? Si no es así, encuentra la ecuación que da la altura final del mercurio en el recipiente.
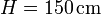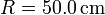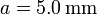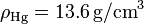Supón que $H = 150\,\mathrm{cm}$ , $R = 50.0\,\mathrm{cm}$ , $a = 5.0\,\mathrm{mm}$ y $\rho_\mathrm{Hg} = 13.6\,\mathrm{g}/\mathrm{cm}^3$ . Calcula el valor numérico del apartado anterior y la cantidad de mercurio que ha salido del recipiente.

2 Presión del aire

Cuando el depósito se va vaciando, el tamaño de la cámara de aire va aumentando. Al aumentar el volumen, manteniéndose constante la temperatura, disminuye la presión, cumpliéndose la ley de Boyle

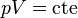
$pV = \mathrm{cte}\,$

El volumen es inicialmente el de un cilindro de altura $H / 2$ y posteriormente $H / 2 + z$ , por lo que la presión es

$p(z) = \frac{p_0V_0}{V(z)} = \frac{p_0AH/2}{A(H-z)} = \frac{p_0H}{2H-2z}$

La presión del gas coincide inicialmente con la atmosférica, pero si el depósito se vacía por completo, la presión se reduce a la mitad.

La diferencia de presiones entre el extremo inferior, abierto a la atmósfera, y el nivel superior es

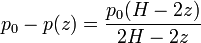
$p_0-p(z) = \frac{p_0(H-2z)}{2H-2z}$

3 Velocidad de salida

Podemos calcular la velocidad de salida aplicando la ley de Bernouilli.

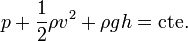
$p + \frac{1}{2}\rho v^2 + \rho g h = \mathrm{cte.}$

Igualando el valor de esta cantidad en 0 y en z, obtenemos

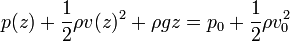
$p(z) + \frac{1}{2}\rho v(z)^2 + \rho g z = p_0 +\frac{1}{2}\rho v_0^2$

La velocidad con la que desciende el nivel del depósito es mucho menor que la que tiene el líquido que sale por el agujero, ya que por la ley de conservación de la masa

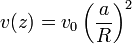
$v(z)\pi R^2 = v_0\pi a^2\,$ $\Rightarrow$ $v(z) = v_0\left(\frac{a}{R}\right)^2$

En concreto, para los datos de este problema, esta proporción es

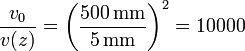
$\frac{v_0}{v(z)} = \left(\frac{500\,\mathrm{mm}}{5\,\mathrm{mm}}\right)^2 = 10000$

Por ello, podemos aproximar $v (z)$ por cero y hallar la velocidad de salida como

$v(z) = \sqrt{2 g z -\frac{2(p_0-p(z))}{\rho}} = \sqrt{2gz-\frac{p_0(H-2z)}{\rho(H-z)}}$

4 Vaciado parcial

La expresión anterior no es siempre positiva. Inicialmente la diferencia de presiones entre el orificio y la superficie superior es nula y la presión hidrostática es la única fuerza que empuja el líquido, pero a medida que el aire se expande y su presión se reduce, aparece una fuerza que se opone al vaciado del recipiente.

Llega un momento en que este efecto vence a la presión hidrostática. Si en la expresión de la velocidad hacemos $z = 0$ (vaciado completo), el radicando se hace negativo, lo que es absurdo. Existe algún valor intermedio de $z$ para el cual la velocidad de salida se anula, momento en el que cesa de vaciarse el depósito. Esto ocurre si

$2gz = \frac{p_0(H-2z)}{\rho(H-z)}$

Agrupando términos obtenemos la ecuación de segundo grado

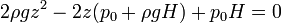
$2\rho g z^2 -2z(p_0+\rho g H) + p_0H=0\,$

5 Valores numéricos

Sustituyendo los valores numéricos del enunciado, en el Sistema Internacional

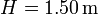
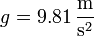
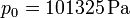
$H = 1.50\,\mathrm{m}$ $\rho = 13600\,\frac{\mathrm{kg}}{\mathrm{m}^3}$ $g=9.81\,\frac{\mathrm{m}}{\mathrm{s}^2}$ $p_0=101325\,\mathrm{Pa}$

obtenemos la ecuación de segundo grado (con $z$ medido en metros)

$266832 z^2 - 602898 z + 151988 = 0\,$

Las soluciones de esta ecuación de segundo grado son

$z_1 = 0.289\,\mathrm{m}$ $z_2 = 1.97\,\mathrm{m}$

La segunda solución no es aceptable, pues el nivel del agua no puede aumentar (y menos aun superar la altura del depósito cerrado herméticamente). Por tanto el nivel mínimo que alcanza el depósito es

$z_\mathrm{min}=28.9\,\mathrm{cm}$

esto es, se vacía un poco más de la mitad del depósito. La cantidad de mercurio que sale es, en volumen, la diferencia entre el volumen inicial y el final

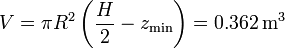
$V = \pi R^2\left(\frac{H}{2}-z_\mathrm{min}\right)=0.362\,\mathrm{m}^3$

En masa, la cantidad de mercurio que sale es

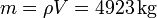
$m = \rho V = 4923\,\mathrm{kg}$

Si en vez de mercurio hubiera sido agua, el descenso del nivel habría sido muy inferior (unos 6 cm) y aun más la masa que sale del depósito.

6 Solución refinada

Este problema puede también resolverse sin hacer la aproximación de que la velocidad del nivel es mucho menor que la de salida del depósito. En ese caso, la ley de Bernouilli nos dice

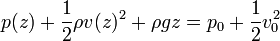
$p(z)+\frac{1}{2}\rho v(z)^2 + \rho g z = p_0+\frac{1}{2}v_0^2$

La velocidad de descenso del nivel la relacionamos con la de salida a través de la ley de conservación de la masa

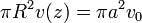
$\pi R^2 v(z)=\pi a^2 v_0\,$

Sustituyendo y despejando

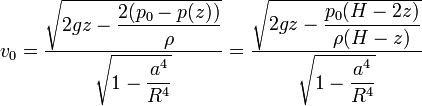
$v_0 = \frac{\sqrt{2gz-\displaystyle\frac{2(p_0-p(z))}{\rho}}}{\sqrt{1-\displaystyle\frac{a^4}{R^4}}}=\frac{\sqrt{2gz - \displaystyle\frac{p_0(H-2z)}{\rho(H-z)}}}{\sqrt{1-\displaystyle\frac{a^4}{R^4}}}$

La condición para hallar el nivel al que deja de vaciarse es exactamente la misma que antes, pues se trata de anular el denominador, que no ha cambiado.

Vaciado de un depósito cilíndrico

De Laplace

Contenido

1 Enunciado

2 Presión del aire

3 Velocidad de salida

4 Vaciado parcial

5 Valores numéricos

6 Solución refinada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES