Velocidad de salida de un depósito
De Laplace
1 Enunciado
Un tanque cerrado contiene un líquido de densidad ρ, y tiene un orificio lateral a una distancia y1 del fondo. El diámetro del orificio es pequeño en comparación con el diámetro del tanque. El aire del interior del tanque que está encima del líquido se encuentra a una presión p. Considera que se trata de un flujo laminar sin fricción.
- Demuestra que la velocidad a la que el fluido sale por el orificio cuando la superficie del líquido está a una altura h respecto a él es
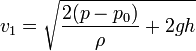
- Considera el caso p = p0. Calcula la distancia a la que llega el agua que sale del orificio en función de y2 y h. Supongamos que podemos variar la altura del orificio. Para un valor fijo de y2, ¿qué valor de h hace máxima la distancia que alcanza el chorro?
2 Velocidad de salida
El principio de Bernouilli estable que para dos puntos situados en la misma línea de corriente
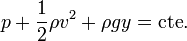
Consideremos entonces un punto “2” situado en la superficie superior del líquido y un punto “1” en el orificio, de forma que el líquido se mueve desde uno hacia el otro. En este caso, la relación anterior da
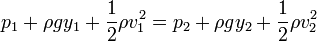
Para el punto 2 la presión es p, la del gas que se encuentra en la cámara superior, la altura respecto al fondo es y2 y la velocidad es la de descenso del nivel del depósito. Si suponemos que esta es muy pequeña, porque el tanque tiene una sección grande y el orificio es pequeño, podemos despreciarla.
Para el punto 1 la presión es la atmosférica, p0, la altura es y1 y la velocidad es v, la de salida. Sustituyendo queda
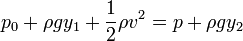
Despejando
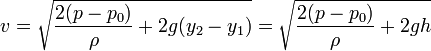
3 Alcance del chorro
Si la presión en la parte superior del líquido es la atmosférica (por ejemplo, porque el depósito no tiene tapa), la expresión anterior se reduce a
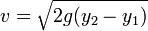
Una vez que sale del depósito, el líquido sigue una trayectoria parabolica, en la que la posición inicial tiene una altura y1 y una velocidad horizontal v. A partir de ahí, la trayectoria del chorro es
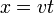
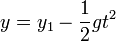
El líquido llega al suelo cuando y = 0, lo que ocurre en el instante
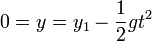

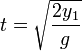
y el alcance del chorro lo da el valor de x en este instante
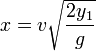
Sustituyendo el valor de la velocidad de salida
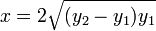
¿Para que altura es máximo el alcance?
Eliminamos la raíz, elevando al cuadrado
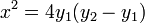
El máximo se da cuando
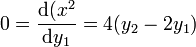

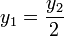
es decir, cuando el orificio está a media altura del depósito. El alcance máximo es
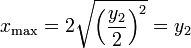
igual al nivel del liquido en el depósito.






