Fundamentos matemáticos
De Laplace
1 Introducción
2 Sistemas de coordenadas cartesianas, cilíndricas y esféricas
3 Campos escalares y vectoriales
4 Gradiente
Dado un campo escalar  , su gradiente,
, su gradiente, 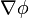 , es un campo vectorial definido como el único vector que dados dos puntos vecinos
, es un campo vectorial definido como el único vector que dados dos puntos vecinos  y
y 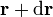 , permite hallar el diferencial de φ como
, permite hallar el diferencial de φ como
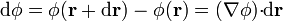
A partir de esta definición se obtiene que la expresión de 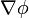 en un sistema coordenado ortogonal es
en un sistema coordenado ortogonal es
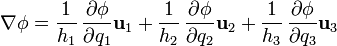
con aplicación inmediata a los tres sistemas más comunes.
Este vector puede leerse como la aplicación de un operador vectorial  (llamado operador nabla) al campo escalar, siendo
(llamado operador nabla) al campo escalar, siendo
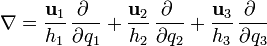
Entre las propiedades del gradiente destaca la de ser normal a las superficies equipotenciales.
Del campo 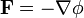 se dice que deriva del potencial escalar
se dice que deriva del potencial escalar  .
.
5 Flujo y divergencia
5.1 Flujo de un campo vectorial
El flujo de un campo vectorial  a través de una superficie abierta S se define como
a través de una superficie abierta S se define como
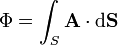
y puede entenderse como una medida de la cantidad de campo que atraviesa dicha superficie (gráficamente, como el número de líneas de campo que atraviesan S).
De manera análoga se define el flujo a través de una superficie cerrada  , que encierra un volumen τ
, que encierra un volumen τ
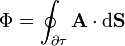
donde en este caso 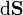 apunta siempre hacia el exterior de la superficie, midiendo el flujo la cantidad de campo que escapa hacia el exterior.
apunta siempre hacia el exterior de la superficie, midiendo el flujo la cantidad de campo que escapa hacia el exterior.
5.2 Divergencia
La divergencia, 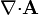 , de un campo vectorial
, de un campo vectorial  se define como el límite, cuando un volumen Δτ se reduce a un punto, del flujo del campo a través de la frontera de Δτ, dividido por el volumen del elemento
se define como el límite, cuando un volumen Δτ se reduce a un punto, del flujo del campo a través de la frontera de Δτ, dividido por el volumen del elemento
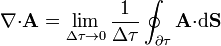
A partir de esta definición puede demostrarse que la divergencia de un campo puede calcularse como la aplicación del operador  escalarmente sobre
escalarmente sobre  . Su expresión en distintos sistemas y en general se indica en la tabla correspondiente.
. Su expresión en distintos sistemas y en general se indica en la tabla correspondiente.
La divergencia de un campo vectorial es un campo escalar ρ, denominado las fuentes escalares de 
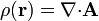
Gráficamente, la divergencia es una medida de si el campo brota de un punto (divergencia positiva), se concentra hacia él (divergencia negativa) o ninguna de las dos cosas (divergencia nula). Un campo que tiene divergencia nula en todos los puntos se denomina campo solenoidal.
La expresión de la divergencia en un sistema de coordenadas ortogonal es relativamente complicada:
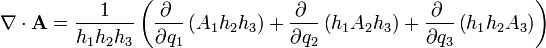
aunque en coordenadas cartesianas se simplifica notablemente:
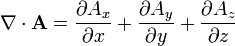
Hay que señalar, no obstante, que el valor de la divergencia es independiente del sistema de coordenadas que se emplee para calcularla.
5.3 Teorema de Gauss
El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss
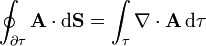
que nos dice que la cantidad de campo que escapa hacia el exterior de una superficie cerrada  es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie.
es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie.
6 Circulación y rotacional
6.1 Circulación de un campo vectorial
La circulación de un campo vectorial 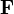 a lo largo de una curva Γ se define como la integral de camino
a lo largo de una curva Γ se define como la integral de camino
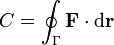
La circulación puede interpretarse como una medida de la rotación neta del campo a lo largo de la curva.
6.2 Rotacional
El rotacional, 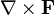 , de un campo vectorial
, de un campo vectorial 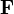 es un vector, cuya componente en un punto
es un vector, cuya componente en un punto  , según la dirección dada por un vector unitario
, según la dirección dada por un vector unitario 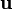 es
es
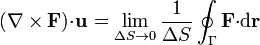
siendo Γ una curva que se reduce a un punto, y ΔS el área delimitada por la curva. La dirección normal al plano de la curva es la dada por 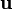 y la orientación la que establece la regla de la mano derecha.
y la orientación la que establece la regla de la mano derecha.
A partir de la definición se deduce que el rotacional se puede calcular como la aplicación del operador nabla como un producto vectorial sobre 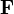 .
.
El campo vectorial que se obtiene a partir de 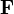 hallando su rotacional en cada punto se denomina como fuentes vectoriales de
hallando su rotacional en cada punto se denomina como fuentes vectoriales de 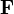 . Un campo cuyas fuentes vectoriales son nulas se conoce como irrotacional o potencial.
. Un campo cuyas fuentes vectoriales son nulas se conoce como irrotacional o potencial.
La expresión general del rotacional en coordenadas curvilíneas puede hallarse mediante el producto vectorial simbólico
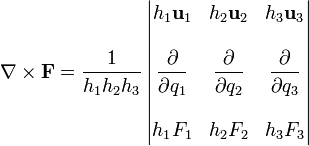
que para el sistema cartesiano se reduce a
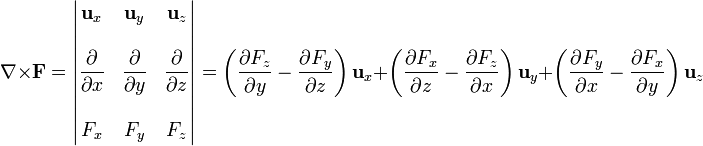
6.3 Teorema de Stokes
La circulación a lo largo de una curva cerrada Γ y el rotacional de un campo vectorial están relacionados por el teorema de Stokes
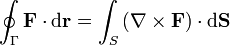
siendo S una superficie arbitraria que tiene a Γ por borde, y cuyo vector normal verifica la regla de la mano derecha respecto al recorrido de Γ.
7 Otros operadores de primer orden
8 Otros teoremas vectoriales
9 Operadores de segundo orden
10 Ángulo sólido
11 Delta de Dirac
12 Potenciales
12.1 Potencial escalar
Un campo irrotacional en una región τ del espacio es aquel cuyo rotacional es nulo en dicha región
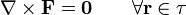
Un campo de este tipo puede expresarse, en dicha región, como el gradiente de un campo escalar, conocido como el potencial escalar del cual deriva dicho campo.
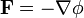
(el signo negativo es cuestión de convenio). Para un campo 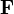 el potencial escalar no es único, ya que siempre se puede obtener un segundo potencial escalar sumándole una constante
el potencial escalar no es único, ya que siempre se puede obtener un segundo potencial escalar sumándole una constante
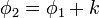

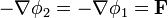
Para evitar ambigüedades, en cada problema donde se necesite usar el potencial escalar, es necesario definir el origen de potencial, que es aquel punto  del espacio en que el potencial escalar es nulo,
del espacio en que el potencial escalar es nulo, 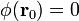 .
.
El potencial escalar puede calcularse a partir del campo vectorial 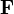 mediante la integral
mediante la integral
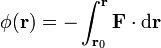
El ejemplo más importante de potencial escalar es el potencial eléctrico, del cual deriva el campo electrostático.
12.2 Potencial vector
Un campo solenoidal en una región τ del espacio es aquel cuya divergencia es nula en dicha región

Un campo de este tipo puede expresarse, en dicha región, como el rotacional de un campo vectorial, conocido como el potencial vector  del cual deriva dicho campo.
del cual deriva dicho campo.

Para un campo 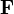 el potencial vector no es único, ya que siempre se puede obtener un segundo potencial vector sumándole el gradiente de un campo escalar arbitrario
el potencial vector no es único, ya que siempre se puede obtener un segundo potencial vector sumándole el gradiente de un campo escalar arbitrario
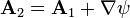


El ejemplo más importante de potencial vector es el potencial vector magnético, del cual deriva el campo magnético.





