Ecuaciones de Maxwell y teorema de Poynting

De Laplace

Revisión a fecha de 13:23 19 may 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Corriente de desplazamiento
2 Ecuaciones de Maxwell
3 La fuerza de Lorentz
4 Energía en un campo electromagnético. Teorema de Poynting
5 Expresión de las ecuaciones de Maxwell en función de los potenciales
6 Problemas

1 Corriente de desplazamiento

La ley de Ampère, tal como se escribe en magnetostática, es incompatible con la ley de conservación de la carga en situaciones variables en el tiempo. Para completarla, es necesario introducir un nuevo término, denominado densidad de corriente de desplazamiento

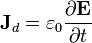
$\mathbf{J}_d = \varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$

de forma que la ley de Ampère pasa a ser la ley de Ampère-Maxwell

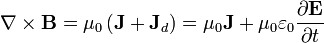
$\nabla\times\mathbf{B} = \mu_0\left(\mathbf{J}+\mathbf{J}_d\right)= \mu_0\mathbf{J}+\mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$

con validez general. En forma integral, esta ecuación indica que la circulación del campo magnético debe incluir un término asociado al flujo eléctrico,

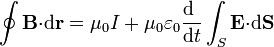
$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = \mu_0 I +\mu_0\varepsilon_0\frac{\mathrm{d}\ }{\mathrm{d}t}\int_S \mathbf{E}{\cdot}\mathrm{d}\mathbf{S}$

La condición de salto para el campo magnético, en cambio, no se ve modificada

$\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}$

La ley de Ampère-Maxwell predice que los campos eléctricos variables en el tiempo son fuente de campos magnéticos. Combinada con la ley de Faraday, que predice el efecto inverso, se llega a que son posibles las ondas electromagnéticas.

Como consecuencia los campos eléctrico y magnético se convierten en inseparables y pueden verse como componentes de un solo campo, denominado campo electromagnético.