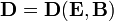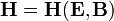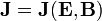Ecuaciones de Maxwell y teorema de Poynting

De Laplace

Contenido

1 Corriente de desplazamiento
2 Ecuaciones de Maxwell
3 Ley de Lorentz
4 Ecuaciones de Maxwell en la materia
5 Energía en un campo electromagnético. Teorema de Poynting
6 Expresión de las ecuaciones de Maxwell en función de los potenciales
7 Problemas

1 Corriente de desplazamiento

La ley de Ampère, tal como se escribe en magnetostática, es incompatible con la ley de conservación de la carga en situaciones variables en el tiempo. Para completarla, es necesario introducir un nuevo término, denominado densidad de corriente de desplazamiento

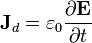
$\mathbf{J}_d = \varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$

de forma que la ley de Ampère pasa a ser la ley de Ampère-Maxwell

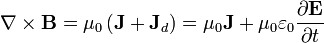
$\nabla\times\mathbf{B} = \mu_0\left(\mathbf{J}+\mathbf{J}_d\right)= \mu_0\mathbf{J}+\mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$

con validez general. En forma integral, esta ecuación indica que la circulación del campo magnético debe incluir un término asociado al flujo eléctrico,

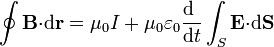
$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = \mu_0 I +\mu_0\varepsilon_0\frac{\mathrm{d}\ }{\mathrm{d}t}\int_S \mathbf{E}{\cdot}\mathrm{d}\mathbf{S}$

La condición de salto para el campo magnético, en cambio, no se ve modificada

$\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}$

La ley de Ampère-Maxwell predice que los campos eléctricos variables en el tiempo son fuente de campos magnéticos. Combinada con la ley de Faraday, que predice el efecto inverso, se llega a que son posibles las ondas electromagnéticas.

Como consecuencia los campos eléctrico y magnético se convierten en inseparables y pueden verse como componentes de un solo campo, denominado campo electromagnético.

2 Ecuaciones de Maxwell

Artículo completo: Ecuaciones de Maxwell

Con la introducción del término de la corriente de desplazamiento, el conjunto de cuatro ecuaciones para el campo electromagnético, conocidas como ecuaciones de Maxwell, junto con sus correspondientes condiciones de salto es el siguiente:

Nombre	Ecuación	Condición
Ley de Gauss	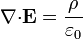$\nabla{\cdot}\mathbf{E} = \frac{\rho}{\varepsilon_0}$	$\mathbf{n}{\cdot}[\mathbf{E}]= \frac{\sigma_s}{\varepsilon_0}$
Ley de Faraday	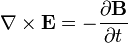$\nabla\times\mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$	$\mathbf{n}\times[\mathbf{E}]=\mathbf{0}$
Ley de Gauss para el campo magnético	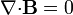$\nabla{\cdot}\mathbf{B} = 0$	$\mathbf{n}{\cdot}[\mathbf{B}]=0\,$
Ley de Ampère-Maxwell	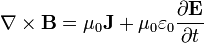$\nabla\times\mathbf{B} = \mu_0\mathbf{J} + \mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}$	$\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}$

A su vez, se denominan ecuaciones homogéneas a la ley de Faraday y la de Gauss para el campo magnético, e inhomogéneas (porque aparecen las fuentes) a la de Gauss y la de Ampère-Maxwell.

Por último, dado que estas ecuaciones incluyen derivadas respecto al tiempo, deben ser suplementadas con las condiciones iniciales correspondientes.

Las ecuaciones de Maxwell describen el comportamiento de los campos electromagnéticos producidos por densidades de carga y de corriente.

3 Ley de Lorentz

Para describir la acción de los campos electromagnéticos sobre la materia, hay que añadir a las ecuaciones de Maxwell la ley para la fuerza.

Para una carga puntual,

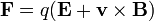
$\mathbf{F} = q(\mathbf{E}+\mathbf{v}\times\mathbf{B})$

Esta ley se extiende a una distribución de carga y de corrientes como

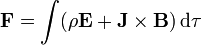
$\mathbf{F} = \int (\rho\mathbf{E} + \mathbf{J}\times\mathbf{B})\,\mathrm{d}\tau$

4 Ecuaciones de Maxwell en la materia

La expresión anterior de las ecuaciones de Maxwell, aun siendo general, incluye términos que a menudo son desconocidos a priori. La densidad de carga $ρ$ incluye la carga de polarización, mientras que la densidad de corriente 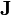$\mathbf{J}$ incluye tanto la densidad de corriente de magnetización como la de polarización

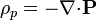
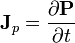
$\rho_p =-\nabla{\cdot}\mathbf{P}$ $\mathbf{J}_p = \frac{\partial \mathbf{P}}{\partial t}$ $\mathbf{J}_m = \nabla\times\mathbf{M}$

Estas densidades pueden hacerse desaparecer de las ecuaciones definiendo los campos auxiliares $\mathbf{D}$ y $\mathbf{H}$

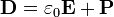
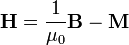
$\mathbf{D} = \varepsilon_0\mathbf{E} + \mathbf{P}$ $\mathbf{H} = \frac{1}{\mu_0}\mathbf{B}-\mathbf{M}$

De esta forma, las ecuaciones de Maxwell se expresan en una forma más reducida

El subíndice $l$ indica que se trata de densidades libres. A menudo se omite este subíndice y es la forma de las ecuaciones la que indica si se habla de densidad de carga libre o total.

En medios materiales se denomina densidad de corriente de desplazamiento al vector

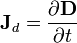
$\mathbf{J}_d = \frac{\partial \mathbf{D}}{\partial t}$

aunque incluye tanto la corriente de desplazamiento en el vacío como la corriente de polarización.

En esta versión las ecuaciones de Maxwell no son completas, sino que deben incluirse relaciones constitutivas que liguen unos campos con otros

$\mathbf{D} = \mathbf{D}(\mathbf{E},\mathbf{B})\,$ $\mathbf{H}=\mathbf{H}(\mathbf{E},\mathbf{B})\,$ $\mathbf{J} = \mathbf{J}(\mathbf{E},\mathbf{B})\,$