Problemas de Ecuaciones de Maxwell

De Laplace

Contenido 1 Campos en un condensador en CA 2 Nube de carga de radio variable 3 Teorema de Poynting para un condensador 4 Teorema de Poynting en un cable coaxial 5 Campos eléctricos y magnéticos debidos a un tubo de corriente 6 Cálculo de fuentes del campo electromagnético 7 Fuentes y fuerza de un posible campo electromagnético 8 Energía electromagnética en una onda viajera 9 Energía electromagnética en una onda estacionaria 10 Flujo de energía alrededor de un dipolo magnético cargado 11 Flujo de energía en un sistema de corriente estacionaria

1 Campos en un condensador en CA

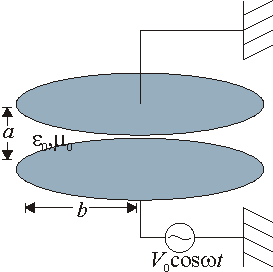
Se tiene un condensador formado por dos placas circulares planas y paralelas, de radio b y separadas una distancia a (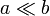); entre ellas hay vacío. Entre los centros de las placas se establece una tensión V₀cosωt.

1. Halle, en primera aproximación, el campo eléctrico que se establece entre las placas.
2. Determine el campo magnético inducido en el espacio entre las placas, según la ley de Ampère-Maxwell.
3. Calcule, la primera corrección en el campo eléctrico obtenido en (1), de acuerdo con la ley de Faraday. ¿Para qué valor del radio empieza a ser importante esta corrección (esto es, comparable al campo estático)?
4. Indique como serían las siguientes correcciones, tanto en como en .

2 Nube de carga de radio variable

Una nube esférica de carga (compuesta de una distribución de cargas puntuales flotando en el vacío) se contrae y dilata, variando el radio de la esfera como R(t) = R₀ + acos(ωt). La carga total de la nube, Q₀, se encuentra distribuida en todo momento de forma uniforme en el volumen de la esfera.

A partir de la ley de conservación de la carga, calcule la densidad de corriente de conducción en la nube. Puede suponer que 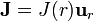y que esta densidad no es infinita en el centro de la esfera.

Calcule el campo eléctrico en los puntos del espacio y, a partir de éste, la corriente de desplazamiento. ¿Cuánto vale la densidad de corriente total?

¿Habrá campo magnético en el sistema?

3 Teorema de Poynting para un condensador

El espacio entre dos placas circulares perfectamente conductoras, planas y paralelas, se encuentra lleno de un material óhmico, de permitividad , conductividad σ, y permeabilidad magnética μ. El radio de las placas es b, y la distancia entre ellas es a (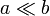). La placa superior está permanentemente a tierra, mientras que el centro de la inferior se encuentra a una tensión V(t).

1. Despreciando los efectos de borde y la inducción electromagnética, halle el campo eléctrico entre las placas y la corriente total que fluye entre ellas.
2. Calcule el campo magnético entre las placas, teniendo en cuenta que en el eje .
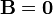3. Halle el vector de Poynting en el espacio entre las placas, así como su flujo a través de una superficie cilíndrica de radio b y altura a, concéntrica con el sistema.
4. ¿A qué equivale este flujo del vector de Poynting? ¿En qué caso es nulo? ¿Qué representa este caso?

4 Teorema de Poynting en un cable coaxial

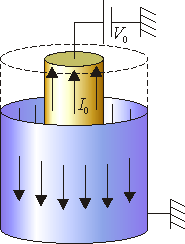
Un cable coaxial ideal está formado por un cilindro interior, de radio a, perfectamente conductor, y una superficie cilíndrica exterior, de radio b, también perfectamente conductora. Los cilindros se extienden indefinidamente a lo largo de su eje.

El cilindro interior se encuentra a una tensión V₀, mientras que la superficie exterior se encuentra a tierra. Simultáneamente, por la superficie del núcleo fluye una corriente I₀ en la dirección del eje, distribuida uniformemente. Esta corriente retorna por la superficie exterior, con lo que hay distribuida uniformemente una corriente − I₀.

1. Halle los campos eléctrico y magnético en todos los puntos del espacio.
2. Calcule las densidades de energía eléctrica y magnética por unidad de volumen, así como la energía total almacenada en una porción de longitud h del cable coaxial.
3. Determine el vector de Poynting en el espacio entre los cilindros. ¿En qué dirección fluye la energía? Halle el flujo de energía a través de una sección del cable coaxial.

5 Campos eléctricos y magnéticos debidos a un tubo de corriente

Un cilindro de radio a y longitud infinita posee una densidad de carga uniforme ρ₀. El cilindro se mueve con velocidad constante 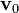paralelamente a su eje, de forma que existe una densidad de corriente 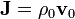. Para todos los puntos del espacio halle:

1. El campo eléctrico, .
2. El campo magnético, .
3. Las densidades de energía eléctrica, 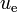, magnética, 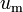y electromagnética, .
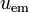4. El vector de Poynting, .
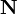5. La velocidad de propagación de la energía, definida como .

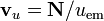6 Cálculo de fuentes del campo electromagnético

Los campos eléctrico y magnético en el interior de un tubo metálico, de sección cuadrada (que se extiende entre − a < x < a y − a < y < a, e indefinidamente a lo largo del eje $z$) vienen dado por las expresiones

En el exterior de este volumen ambos campos son nulos.

1. Pruebe que este campo (, ) verifica todas las ecuaciones y condiciones de salto necesarias para ser un campo electromagnético.
2. Calcule las densidades de carga y de corriente, fuentes de este campo.

7 Fuentes y fuerza de un posible campo electromagnético

En una región del espacio tenemos un par de campos dados por las expresiones, en coordenadas cilíndricas,

        

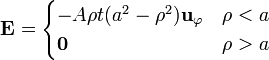
siendo A una constante.

1. Compruebe que se trata de un posible campo electromagnético.
2. Calcule las fuentes de este campo.
3. Determine las densidades volumétricas de energía eléctrica, magnética, electromagnética y de potencia desarrollada por el campo.
4. Halle la fuerza sobre una carga puntual que en el instante t = a / c se encuentra situada en el punto 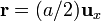y se mueve con una velocidad 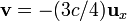(siendo la velocidad de la luz).

8 Energía electromagnética en una onda viajera

Una onda plana monocromática en una región libre de fuentes posee el campo eléctrico

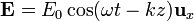
1. Determine el valor del campo magnético en todos los puntos del espacio.
2. Calcule las densidades de energía eléctrica y magnética en todos los puntos del espacio.
3. Halle el promedio temporal de las densidades de energía, definido como

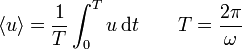
4. Calcule el vector de Poynting en cada instante
5. Halle el promedio temporal del vector de Poynting

9 Energía electromagnética en una onda estacionaria

Una onda estacionaria monocromática en una región libre de fuentes posee el campo eléctrico

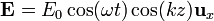
1. Determine el valor del campo magnético en todos los puntos del espacio.
2. Calcule las densidades de energía eléctrica y magnética en todos los puntos del espacio.
3. Halle el promedio temporal de las densidades de energía, definido como

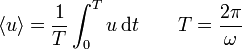
4. Calcule el vector de Poynting en cada instante
5. Halle el promedio temporal del vector de Poynting

10 Flujo de energía alrededor de un dipolo magnético cargado

Suponga un pequeño imán (modelable por un dipolo magnético ) en cuyo interior hay una carga eléctrica q.

1. Calcule las densidades de energía eléctrica y magnética en el sistema.
2. Determíne el vector de Poynting en cada punto del espacio. ¿Cómo se interpreta en este sistema el flujo de energía?
3. Compruebe que se verifica el teorema de Poynting en forma diferencial.

11 Flujo de energía en un sistema de corriente estacionaria

Considere el siguiente sistema: una chapa cilíndrica de radio a y espesor c, muy pequeño comparado con el radio, y de gran longitud. El material de la lámina posee conductividad σ. La chapa no forma un cilindro cerrado, sino que presenta un corte a todo lo largo. Entre los dos extremos del corte se establece una tensión continua V₀.

1. Como consecuencia de la tensión aplicada y del hecho de que el material es conductor, fluirá una corriente por la placa. Determine la densidad de corriente, así como el campo y el potencial en los puntos de la placa.
2. Halle la potencia disipada en el medio conductor, por unidad de volumen y en una sección circular del cilindro.
3. Dado que el potencial es una función continua, el resultado obtenido en el apartado anterior sirve para establecer condiciones de contorno para el potencial eléctrico en el exterior y el interior de la superficie cilíndrica. Plantee las ecuaciones y condiciones de contorno para el potencial en estas regiones.
4. Resuelva los problemas de potencial anteriores, usando el método de separación de variables. Suponga que no existe dependencia en la coordenada z, por lo que el problema es, en realidad, bidimensional.
5. Las expresiones en forma de serie para los potenciales eléctricos dentro y fuera son sumables y expresables como funciones sencillas. Determine estas funciones
6. Calcule el campo eléctrico y la densidad de carga en todos los puntos del espacio.
7. El sistema es al mismo tiempo un solenoide circular. Halle el campo magnético interior y exterior del cilindro.
8. Conocidos los campos eléctrico y magnético, determine el vector de Poynting en la región interior y la exterior. ¿De dónde y hacia dónde puede interpretarse que fluye la energía?
9. Calcule el flujo del vector de Poynting a través de un plano situado en x = x₀. Distinga los casos | x | < a y | x | > a.