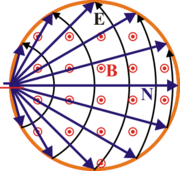
Flujo de energía en un sistema de corriente estacionaria

De Laplace

1 Enunciado

Considere el siguiente sistema: una chapa cilíndrica de radio

a

y espesor

c

, muy pequeño comparado con el radio, y de gran longitud. El material de la lámina posee conductividad

σ

. La chapa no forma un cilindro cerrado, sino que presenta un corte a todo lo largo. Entre los dos extremos del corte se establece una tensión continua

V 0

.

Como consecuencia de la tensión aplicada y del hecho de que el material es conductor, fluirá una corriente por la placa. Determine la densidad de corriente, así como el campo y el potencial en los puntos de la placa.
Halle la potencia disipada en el medio conductor, por unidad de volumen y en una sección circular del cilindro.
Dado que el potencial es una función continua, el resultado obtenido en el apartado anterior sirve para establecer condiciones de contorno para el potencial eléctrico en el exterior y el interior de la superficie cilíndrica. Plantee las ecuaciones y condiciones de contorno para el potencial en estas regiones.
Resuelva los problemas de potencial anteriores, usando el método de separación de variables. Suponga que no existe dependencia en la coordenada $z$ , por lo que el problema es, en realidad, bidimensional.
Las expresiones en forma de serie para los potenciales eléctricos dentro y fuera son sumables y expresables como funciones sencillas. Determine estas funciones
Calcule el campo eléctrico y la densidad de carga en todos los puntos del espacio.
El sistema es al mismo tiempo un solenoide circular. Halle el campo magnético interior y exterior del cilindro.
Conocidos los campos eléctrico y magnético, determine el vector de Poynting en la región interior y la exterior. ¿De dónde y hacia dónde puede interpretarse que fluye la energía?
Calcule el flujo del vector de Poynting a través de un plano situado en $x = x 0$ . Distinga los casos $| x | < a$ y $| x | > a$ .

2 Introducción

Este problema ilustra, como el del flujo de energía alrededor de un dipolo cargado, la posibilidad de que en un sistema estacionario el vector de Poynting sea no nulo y por tanto exista un flujo de energía, con la diferencia respecto al otro problema, de que aquí si hay producción de energía electromagnética en un punto del sistema y consumo en otro, viajando la energía del primero al segundo.

Concretamente, tenemos un medio óhmico por el que circula una cierta corriente y en el que se disipa energía por efecto Joule, y un generador de corriente continua que alimenta dicha corriente. La energía electromagnética es producida en el generador y consumida en la resistencia.

Una primara intuición sugeriría que la energía fluye desde la fuente hasta la resistencia por el cable que las conecta. Sin embargo, como veremos, no es así. De acuerdo con el teorema de Poynting viaja por el aire y entra en la resistencia desde el exterior por sus paredes.

3 Potencial en la superficie cilíndrica

Esquema y coordenadas

Para determinar la distribución de potencial a lo largo de la superficie resistiva, situamos un sistema de ejes de forma que el eje Z coincide con el del cilindro, el eje X es el perpendicular a éste que pasa por el punto donde se encuentra la fuente y el Y el ortogonal a ambos. De esta forma, la fuente de tensión se encuentra sobre la línea $x = - a$ , $y = 0$ .

Dada la gran longitud del sistema, podemos suponer simetría traslacional

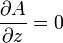
$\frac{\partial A}{\partial z}=0$

para todas las magnitudes, con lo que el problema se reduce a uno bidimensional.

Si empleamos coordenadas cilíndricas, la fuente se encuentra en $ρ = a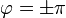$ , $\varphi=\pm \pi$ . El problema del potencial dentro del material óhmico es el siguiente:

Por tratarse de un medio homogéneo en estado estacionario se verifica la ecuación de Laplace

$\nabla^2\phi = 0$

Existe una diferencia de potencial $V 0$ entre ambos lados de la fuente, lo que, por simetría, podemos escribir

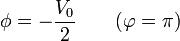
$\phi = +\frac{V_0}{2}\qquad(\varphi=-\pi)$ $\phi = -\frac{V_0}{2}\qquad(\varphi=\pi)$

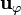El criterio de signos lo hemos tomado de forma que la corriente circule en sentido antihorario, esto es, en la dirección de $\mathbf{u}_\varphi$ .

En las paredes de la corona cilíndrica la corriente normal es nula

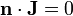
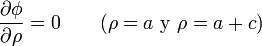
$\mathbf{n}\cdot\mathbf{J}=0\,$ $\Rightarrow$ $\frac{\partial\phi}{\partial \rho}=0\qquad(\rho=a\ \mbox{y}\ \rho=a+c)$

Por la simetría traslacional tenemos que el potencial no depende de la coordenada $z$ . La condición de contorno en las paredes sugiere hacer la hipótesis de que el potencial tampoco depende de la coordenada radial. En ese caso la ecuación de Laplace en cilíndricas se reduce a

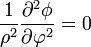
$\frac{1}{\rho^2}\frac{\partial^2\phi}{\partial \varphi^2}=0$

de donde

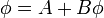
$\phi = A + B \phi\,$

Imponiendo ahora las condiciones de contorno

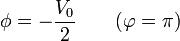
$\phi = +\frac{V_0}{2}\qquad(\varphi=-\pi)$ $\phi = -\frac{V_0}{2}\qquad(\varphi=\pi)$

obtenemos

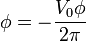
$\phi = -\frac{V_0\phi}{2\pi}$

4 Potencia disipada

Una vez que tenemos la distribución de potencial en el medio óhmico, hallamos el campo eléctrico

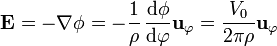
$\mathbf{E}=-\nabla\phi = -\frac{1}{\rho}\,\frac{\mathrm{d}\phi}{\mathrm{d}\varphi}\mathbf{u}_\varphi=\frac{V_0}{2\pi \rho}{\mathbf{u}_\varphi}$

Puesto que la lámina es muy delgada, podemos suponer que 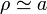$\rho\simeq a$ para todos sus puntos y aproximar el campo por

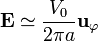
$\mathbf{E}\simeq \frac{V_0}{2\pi a}\mathbf{u}_\varphi$

esto es, que si se desprecian los efectos de curvatura resulta un campo igual a la diferencia de potencial dividida por la distancia.

La densidad de corriente la obtenemos de la ley de Ohm

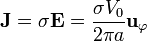
$\mathbf{J}=\sigma \mathbf{E}=\frac{\sigma V_0}{2\pi a}\mathbf{u}_\varphi$

La poten cia dispada por unidad de volumen en el medio óhmico la da la ley de Joule

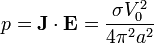
$p = \mathbf{J}\cdot\mathbf{E}=\frac{\sigma V_0^2}{4\pi^2 a^2}$

Por ser uniforme la potencia total disipada en una porción de cilindro de altura $h$ será igual al producto de esta densidad por el volumen de una corona cilíndrica

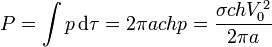
$P = \int p\,\mathrm{d}\tau = 2\pi a c h p = \frac{\sigma c h V_0^2}{2\pi a}$

Esta potencia es igual a la consumida en una resistencia filiforme de valor

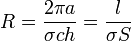
$R = \frac{2\pi a}{\sigma c h}=\frac{l}{\sigma S}$

La potencia consumida por unidad de longitud del cilindro es

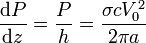
$\frac{\mathrm{d}P}{\mathrm{d}z}=\frac{P}{h}= \frac{\sigma cV_0^2}{2\pi a}$

5 Problema del potencial en el vacío

Lo anterior nos da el potencial en el interior del medio óhmico, pero, ¿qué ocurre en el espacio que lo rodea? Podría pensarse, erróneamente, que puesto que solo hay corriente en el medio óhmico, solo existe campo en él. Pero esto es incorrecto. Puesto que existe una diferencia de potencial entre los diferentes puntos del cilindro, debe haber un campo eléctrico que vaya de los puntos de mayor potencial a los de menor, tanto por dentro como por fuera del material.

¿Dónde están las fuentes de este campo? Puesto que el campo en el material óhmico es puramente tangencial a su superficie, mientras que en el espacio que lo rodea no lo será en general, existe una discontinuidad en la componente normal del campo eléctrico y por tanto una densidad de carga superficial. Es esta densidad de carga superficial la que desvía la corriente, haciéndola girar siguiendo a la superficie cilíndrica. Es también la que produce el campo eléctrico en el espacio interior y exterior a la superficie cilíndrica.

Esta superficie cilíndrica divide al espacio en dos regiones, la interior ( $ρ < a$ ) y la exterior ( $ρ > a$ ). En cada una de ellas se cumplirá la ecuación de Laplace

$\nabla^2\phi = \frac{1}{\rho}\frac{\partial\ }{\partial\rho}\left(\rho\frac{\partial\phi}{\partial\phi}\right)+\frac{1}{\rho^2}\,\frac{\partial^2\phi}{\partial\varphi^2}=0$

La condición de contorno, tanto para el problema interior como para el exterior, es que el potencial -que es una función continua- valga sobre la superficie cilíndrica la expresión que ya hemos calculado

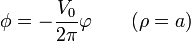
$\phi = -\frac{V_0}{2\pi}\varphi\qquad(\rho=a)$

A esto hay que añadirle, para el potencial exterior, que lejos del cilindro el potencial debe valer cero

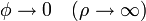
$\phi \to 0 \quad (\rho\to\infty)$

y para el potencial interior, que no puede ser singular en el eje, en el que no hay carga alguna

$\phi\not\to\infty\qquad(\rho\to 0)$

6 Solución del problema del potencial

La ecuación de Laplace en coordenadas cilíndricas, cuando hay simetría traslacional, puede resolverse, de forma sistemática empleando el método de separación de variables. Este método consiste en escribir el potencial como una combinación de funciones base

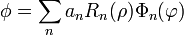
$\phi = \sum_n a_n R_n(\rho)\Phi_n(\varphi)$

Sustituyendo en la ecuación de Laplace y separando los factores dependientes de $ρ$ de los de $\varphi$ se obtiene que las funciones base son de la forma

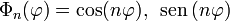
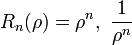
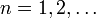
$\Phi_n(\varphi)=\cos(n\varphi),\ \,\mathrm{sen}\,(n\varphi)$ $R_n(\rho)=\rho^n,\ \frac{1}{\rho^n}$ $n=1,2,\ldots\,$

Ahora bien, de todas las posibles soluciones, las condiciones de cada problema permiten descartar algunas de entrada.

En el exterior del cilindro el potencial debe decaer a cero, por lo que las soluciones que crecen con $ρ$ pueden descartarse y

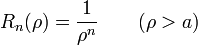
$R_n(\rho) = \frac{1}{\rho^n}\qquad (\rho>a)$

Análogamente, puesto que el potencial no puede divergir en el eje, debemos descartas las soluciones que crecen cuando $\rho\to 0$ y tomar

$R_n(\rho) = \rho^n \qquad (\rho<a)$

En este problema, además, el potencial dado por la condición de contorno es una función impar en $\varphi$ , lo que nos permite descartar los cosenos (que son funciones pares) y quedarnos con

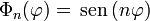
$\Phi_n(\varphi)=\,\mathrm{sen}\,(n\varphi)$

Con todo ello, nos queda que el potencial en el interior del cilindro puede escribirse como la serie

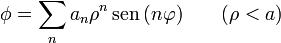
$\phi = \sum_n a_n \rho^n \,\mathrm{sen}\,(n\varphi)\qquad(\rho< a)$

mientras que en el exterior

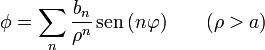
$\phi = \sum_n \frac{b_n}{\rho^n} \,\mathrm{sen}\,(n\varphi)\qquad(\rho> a)$

Con $a n$ y $b n$ constantes aun por determinar.

Para hallar estas constantes, debemos imponer que tanto, po dentro como fuera, en $ρ = a$ debe cumplirse que

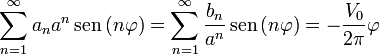
$\sum_{n=1}^\infty a_n a^n \,\mathrm{sen}\,(n\varphi)=\sum_{n=1}^\infty \frac{b_n}{a^n} \,\mathrm{sen}\,(n\varphi)=-\frac{V_0}{2\pi}\varphi$

con lo que el problema se reduce a determinar los coeficientes de la serie de Fourier

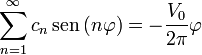
$\sum_{n=1}^\infty c_n\,\mathrm{sen}\,(n\varphi)=-\frac{V_0}{2\pi}\varphi$

Calculamos estos coeficientes multiplicando por 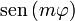$\,\mathrm{sen}\,(m\varphi)$ e integrando. Por un lado tenemos que

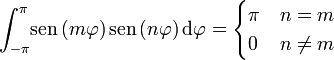
$\int_{-\pi}^\pi\!\mathrm{sen}\,(m\varphi)\,\mathrm{sen}\,(n\varphi)\,\mathrm{d}\varphi=\begin{cases} \pi & n=m\\ 0 &n\neq m\end{cases}$

y por otro

$\int_{-\pi}^\pi \varphi\,\mathrm{sen}\,(m\varphi)\,\mathrm{d}\varphi = \frac{2\pi}{n}(-1)^{n+1}$

Combinado los dos resultados

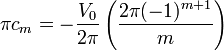
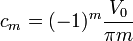
$\pi c_m =-\frac{V_0}{2\pi}\left(\frac{2\pi (-1)^{m+1}}{m}\right)$ $\Rightarrow$ $c_m = (-1)^{m}\frac{V_0}{\pi m}$

La solución para el potencial interior se escribe entonces

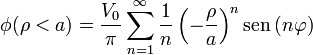
$\phi(\rho<a) = \frac{V_0}{\pi}\sum_{n=1}^\infty \frac{1}{n}\left(-\frac{\rho}{a}\right)^n\mathrm{sen}\,(n\varphi)$

y en el exterior

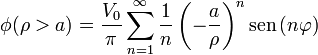
$\phi(\rho>a) = \frac{V_0}{\pi}\sum_{n=1}^\infty \frac{1}{n}\left(-\frac{a}{\rho}\right)^n\mathrm{sen}\,(n\varphi)$

Estos dos resultados se pueden combinar en la expresión

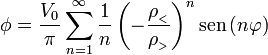
$\phi = \frac{V_0}{\pi}\sum_{n=1}^\infty \frac{1}{n}\left(-\frac{\rho_{_<}}{\rho_{_>}}\right)^n\mathrm{sen}\,(n\varphi)$

donde

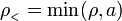
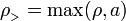
$\rho_{_<} = \min(\rho,a)\,$ $\rho_{_>} = \max(\rho,a)\,$

7 Expresión cerrada

7.1 Fórmula general

Aunque la solución en forma de serie es perfectamente válida, en este caso puede hallarse una solución cerrada, en forma de una sola función.

Para ello, observamos, en primer lugar, que de acuerdo con la fórmula de Euler

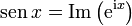
$\mathrm{sen}\,x = \mathrm{Im}\left(\mathrm{e}^{\mathrm{i}x}\right)$

con lo que la serie para el potencial se puede escribir

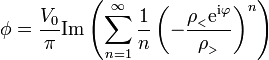
$\phi = \frac{V_0}{\pi}\mathrm{Im}\left(\sum_{n=1}^\infty \frac{1}{n}\left(-\frac{\rho_{_<}\mathrm{e}^{\mathrm{i}\varphi}}{\rho_{_>}}\right)^n\right)$

A continuación hacemos uso de la serie de Taylor

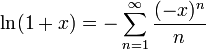
$\ln(1+x) = -\sum_{n=1}^\infty \frac{(-x)^n}{n}$

por lo que el potencial se reduce a

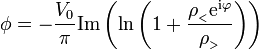
$\phi = -\frac{V_0}{\pi}\mathrm{Im}\left(\ln\left(1+\frac{\rho_{_<}\mathrm{e}^{\mathrm{i}\varphi}}{\rho_{_>}}\right)\right)$

Para hallar esta parte imaginaria aplicamos que, para el logaritmo de un número complejo

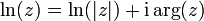
$\ln(z) = \ln(|z|) + \mathrm{i}\arg(z)\,$

siendo el argumento de un número complejo

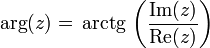
$\arg(z) = \,\mathrm{arctg}\,\left(\frac{\mathrm{Im}(z)}{\mathrm{Re}(z)}\right)$

Por otro lado tenemos que

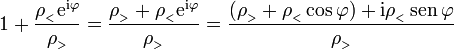
$1+\frac{\rho_{_<}\mathrm{e}^{\mathrm{i}\varphi}}{\rho_{_>}}=\frac{\rho_{_>}+\rho_{_<}\mathrm{e}^{\mathrm{i}\varphi}}{\rho_{_>}}=\frac{(\rho_{_>}+\rho_{_<}\cos\varphi)+\mathrm{i}\rho_{_<}\,\mathrm{sen}\,\varphi}{\rho_{_>}}$

De esta forma, obtenemos finalmente la expresión cerrada para el potencial

$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{\rho_{_<}\,\mathrm{sen}\,\varphi}{\rho_{_>}+\rho_{_<}\cos(\varphi)}\right)$

7.2 Potencial interior

Particularizando los valores

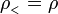
$\rho_{_<}=\rho\,$ $\rho_{_>}=a\,$

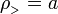
el potencial en el interior del cilindro se escribe

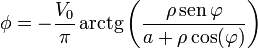
$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{\rho\,\mathrm{sen}\,\varphi}{a+\rho\cos(\varphi)}\right)$

Pasando a coordenadas cartesianas

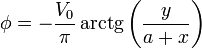
$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{y}{a+x}\right)$

Este resultado posee una sencilla interpretación geométrica. Consideremos el vector en el plano XY que une el punto 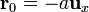$\mathbf{r}_0=-a\mathbf{u}_x$ (donde se encuentra la fuente, con un punto cualquiera del círculo interior. Este vector de posición relativa es

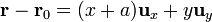
$\mathbf{r}-\mathbf{r}_0=(x+a)\mathbf{u}_x+y\mathbf{u}_y\,$

por tanto el potencial en el interior del cilindro es simplemente

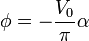
$\phi = -\frac{V_0}{\pi}\alpha$

siendo $α$ el ángulo que forma con el eje X el vector de posición relativa a la fuente.

Gráficamente esto quiere decir que las superficies equipotenciales son bandas verticales, que se abren en abanico desde la fuente y que se extienden desde ésta hasta un punto de la superficie cilíndrica.

En los puntos de la superficie cilíndrica se cumple

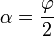
$\alpha = \frac{\varphi}{2}$

con lo que es evidente que se verifica la condición de contorno sobre la superficie interior del cilindro.

7.3 Potencial exterior

Haciendo ahora

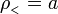
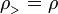
$\rho_{_<}=a\,$ $\rho_{_>}=\rho\,$

el potencial en el exterior del cilindro se escribe

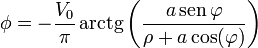
$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{a\,\mathrm{sen}\,\varphi}{\rho+a\cos(\varphi)}\right)$

Para expresar este potencial en coordenadas cartesianas multiplicamos en el numerador y el denominador por $ρ$ y queda

$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{ay}{x^2+y^2+ax}\right)$

Podemos obtener la ecuación de las superficies equipotenciales invirtiendo esta ecuación

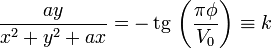
$\frac{ay}{x^2+y^2+ax}=-\,\mathrm{tg}\,\left(\frac{\pi\phi}{V_0}\right)\equiv k$

o, lo que es lo mismo,

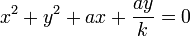
$x^2+y^2+ax + \frac{ay}{k} = 0$

que es la ecuación de una cilindro circular paralelo al eje Z y cuyo eje y radio se obtienen escribiendo esta ecuación como

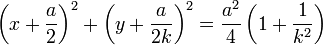
$\left(x+\frac{a}{2}\right)^2+\left(y+\frac{a}{2k}\right)^2 = \frac{a^2}{4}\left(1+\frac{1}{k^2}\right)$

Esto es, el eje se encuentra en

$\mathbf{r}_C = -\frac{a}{2}\mathbf{u}_x+\frac{a}{2}\,\mathrm{cotg}\,\left(\frac{\pi \phi}{V_0}\right)\mathbf{u}_y=\frac{a}{2\,\mathrm{sen}\,(\pi\phi/V_0)}\left(-\,\mathrm{sen}\left(\frac{\pi \phi}{V_0}\right)\mathbf{u}_x+\cos\left(\frac{\pi \phi}{V_0}\right)\mathbf{u}_y\right)$

y el radio es

$R = \frac{a}{2}\sqrt{1+\,\mathrm{cotg}^2\left(\frac{\pi \phi}{V_0}\right)}=\frac{a}{2|\mathrm{sen}\,(\pi \phi/V_0)|}$

Potencial y campo eléctrico

8 Campo eléctrico

8.1 Medio óhmico

Este ya lo calculamos en el primer apartado:

$\mathbf{E}\simeq \frac{V_0}{2\pi a}\mathbf{u}_\varphi\qquad (a<\rho<a+c)$

8.2 Interior del cilindro

El campo en la región interior será el gradiente del potencial en el interior, cambiado de signo:

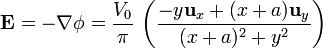
$\mathbf{E}=-\nabla\phi = \frac{V_0}{\pi}\,\left(\frac{-y\mathbf{u}_x+(x+a)\mathbf{u}_y}{(x+a)^2+y^2}\right)$

Este campo es perpendicular a los planos equipotencial y por tanto sus líneas de campo describen arcos de circunferencia en torno del punto donde se encuentra la fuente.

8.3 Exterior del cilindro

La expresión para el campo en el exterior es un poco más complicada. Hallando el gradiente

$\mathbf{E}=\frac{V_0(y(2x+a)\mathbf{u}_x-a(x^2+a x - y^2)\mathbf{u}_y)}{\pi (x^2+y^2)((x+a)^2+y^2)}$

Las líneas de campo para este campo exterior son arcos de circunferencia horizontales centrados en el plano XZ y que conectan dos puntos simétricos del cilindro de corriente.

8.4 Densidad de carga

La densidad volumétrica es nula en todo el espacio, siendo la única densidad de carga la depositada sobre la superficie del cilindro. Ésta la obtenemos a partir de la discontinuidad en la componente normal del campo eléctrico.

8.4.1 Cara interior

En $ρ = a$ tenemos

$\sigma_s = \varepsilon_0\mathbf{n}\cdot[\mathbf{E}]=-\varepsilon_0\mathbf{n}\cdot\left(\nabla\phi(a^+)-\nabla\phi(a^-)\right)$

Dentro del material óhmico el campo es acimutal y el producto escalar se anula. Para el espacio interior al cilindro, el producto escalar deja solo la componente radial del gradiente y por tanto

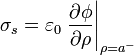
$\sigma_s=\varepsilon_0\left.\frac{\partial\phi}{\partial\rho}\right|_{\rho=a^-}$

Derivando la expresión

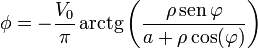
$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{\rho\,\mathrm{sen}\,\varphi}{a+\rho\cos(\varphi)}\right)$

obtenemos

$\sigma_s=-\frac{\varepsilon_0 V_0}{2\pi a}\mathrm{tg}\left(\frac{\varphi}{2}\right)$

Esta densidad de carga es nula en los puntos opuestos a la fuente y a partir de ahí va aumentando en magnitud hasta hacerse infinita, como el campo, en los puntos junto a la fuente. Es positiva en los puntos con 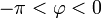$-\pi<\varphi < 0$ y negativa en el otro semiespacio.

8.4.2 Cara exterior

Operando igualmente en $ρ = a + c$ tenemos

$\sigma_s = \varepsilon_0\mathbf{n}\cdot[\mathbf{E}]=-\varepsilon_0\mathbf{n}\cdot\left(\nabla\phi(a^+)-\nabla\phi(a^-)\right)$

Dentro del material óhmico el campo es acimutal y el producto escalar se anula. Para el espacio exterior al cilindro, el producto escalar deja solo la componente radial del gradiente y por tanto

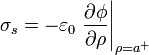
$\sigma_s=-\varepsilon_0\left.\frac{\partial\phi}{\partial\rho}\right|_{\rho=a^+}$

Derivando la expresión

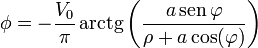
$\phi = -\frac{V_0}{\pi}\,\mathrm{arctg}\left(\frac{a\,\mathrm{sen}\,\varphi}{\rho+a\cos(\varphi)}\right)$

obtenemos de nuevo

$\sigma_s=-\frac{\varepsilon_0 V_0}{2\pi a}\mathrm{tg}\left(\frac{\varphi}{2}\right)$

Por tanto la carga se distribuye por igual a los dos lados del material óhmico.

9 Campo magnético

El campo magnético es mucho más fácil de calcular que el eléctrico.

Puesto que tenemos una delgada superficie cilíndrica de gran longitud por la que circula una corriente uniforme acimutal, el sistema es equivalente a un solenoide infinito, y por tanto el campo magnético producido por él es

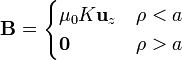
$\mathbf{B}=\begin{cases} \mu_0K\mathbf{u}_z & \rho < a \\ \mathbf{0} & \rho > a\end{cases}$

En este caso la densidad de corriente superficial equivalente es la que recorre una capa de espesor $c$

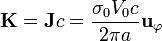
$\mathbf{K}=\mathbf{J}c=\frac{\sigma_0V_0c}{2\pi a} \mathbf{u}_\varphi$

y por tanto el campo magnético es

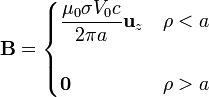
$\mathbf{B}=\begin{cases} \displaystyle\frac{\mu_0\sigma V_0 c}{2\pi a}\mathbf{u}_z & \rho < a \\ & \\ \mathbf{0} & \rho > a\end{cases}$

10 Vector de Poynting

Distribución de los campos y del vector de Poynting

Una vez que tenemos el campo eléctrico y el magnético, podemos calcular el vector de Poynting

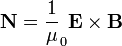
$\mathbf{N}=\frac{1}\mu_0\mathbf{E}\times\mathbf{B}$

En el exterior del cilindro el campo magnético es nulo y por tanto

$\mathbf{N}=\mathbf{0}\qquad (\rho>a)\,$

En el interior

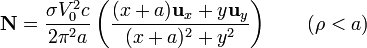
$\mathbf{N}=\frac{\sigma V_0^2c}{2\pi^2 a}\left(\frac{(x+a)\mathbf{u}_x+y\mathbf{u}_y}{(x+a)^2+y^2}\right)\qquad(\rho<a)$

Este vector es perpendicular al campo eléctrico y por tanto tangente a las superficies equipotenciales, esto es, es radial desde el punto donde se encuentra la fuente.

Según esto, la energía viaja desde la fuente hasta el medio óhmico no a lo largo de este material, sino radialmente por el espacio intermedio.

11 Flujo de energía

11.1 Cálculo directo

Para hallar el flujo de energía a través de un plano vertical situado en $x = x 0$ solo hay que considerar la porción de plano contenida dentro del cilindro, por ser nulo el vector de Poynting. Por tanto

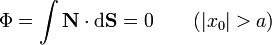
$\Phi = \int \mathbf{N}\cdot\mathrm{d}\mathbf{S}=0\qquad (|x_0|>a)$

Si $| x 0 | < a$ debemos considerar el flujo a través de una banda que se extiende indefinidamente en la dirección del eje Z y desde $- y 0$ a $+ y 0$ con

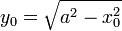
$y_0 = \sqrt{a^2-x_0^2}$

Si consideramos una porción de altura $h$ , esto nos da la integral

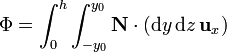
$\Phi = \int_0^h \int_{-y_0}^{y_0} \mathbf{N}\cdot(\mathrm{d}y\,\mathrm{d}z\,\mathbf{u}_x)$

Sustituyendo

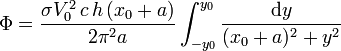
$\Phi = \frac{\sigma V_0^2\,c\,h\,(x_0+a)}{2\pi^2 a}\int_{-y_0}^{y_0}\frac{\mathrm{d}y}{(x_0+a)^2+y^2}$

Esta integral es casi inmediata

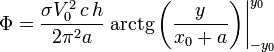
$\Phi = \frac{\sigma V_0^2\,c\,h}{2\pi^2 a}\left.\mathrm{arctg}\left(\frac{y}{x_0+a}\right)\right|_{-y_0}^{y_0}$

Tenemos que

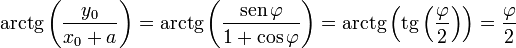
$\mathrm{arctg}\left(\frac{y_0}{x_0+a}\right)=\mathrm{arctg}\left(\frac{\mathrm{sen}\,\varphi}{1+\cos\varphi}\right)=\mathrm{arctg}\left(\mathrm{tg}\left(\frac{\varphi}{2}\right)\right)=\frac{\varphi}{2}$

y por tanto

$\Phi = \frac{\sigma V_0^2 c\,h\,\varphi}{2\pi^2 a}$

Pero este flujo es igual a

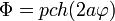
$\Phi = p c h (2a\varphi)\,$

con $p$ la potencia consumida por unidad de volumen el medio óhmico. Tenemos entonces que el flujo del vector de Poynting a través de una sección coincide con la energía que se consume en la porción de cilindro óhmico que queda más allá de este plano.

12 Cálculo indirecto

El flujo del vector de Poynting puede hallarse de una forma que relaciona directamente esta cantidad de la ley de Joule.

Para una superficie podemos construir un vector diferencial de superficie multiplicando vectorialmente dos diferenciales de camino tangentes a la superficie

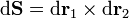
$\mathrm{d}\mathbf{S}=\mathrm{d}\mathbf{r}_1\times\mathrm{d}\mathbf{r}_2\,$

Por tratarse de una superficie vertical, podemos tomar

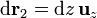
$\mathrm{d}\mathbf{r}_2 = \mathrm{d}z\,\mathbf{u}_z$

y como 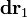$\mathbf{d}\mathbf{r}_1$ un vector tangente a la superficie y contendio en el plano XY. Tenemos entonces

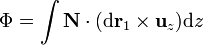
$\Phi = \int \mathbf{N}\cdot(\mathrm{d}\mathbf{r}_1\times\mathbf{u}_z)\mathrm{d}z$

Puesto que este vector de Poynting no depende de la coordenada $z$

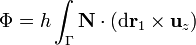
$\Phi = h\int_\Gamma \mathbf{N}\cdot(\mathrm{d}\mathbf{r}_1\times\mathbf{u}_z)$

Por otro lado

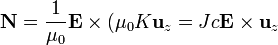
$\mathbf{N}=\frac{1}{\mu_0}\mathbf{E}\times(\mu_0 K\mathbf{u}_z=Jc\mathbf{E}\times\mathbf{u}_z$

Sustituyendo esto en la integral

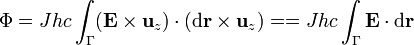
$\Phi = Jhc\int_\Gamma(\mathbf{E}\times\mathbf{u}_z)\cdot(\mathrm{d}\mathbf{r}\times\mathbf{u}_z)= = Jhc\int_\Gamma \mathbf{E}\cdot\mathrm{d}\mathbf{r}$

La integral de camino del campo eléctrico es simplemente la diferencia de potencial y $J h c$ es la intensidad de corriente que fluye por una sección del tubo. Por tanto

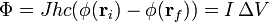
$\Phi = Jhc(\phi(\mathbf{r}_i)-\phi(\mathbf{r}_f)) = I\,\Delta V$

esto es, independientemente de qué sección se tome, plana o curvada, el flujo del vector de Poynting coincide con la potencia consumida más allá de dicha superficie.