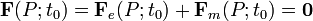Fuentes y fuerza de un posible campo electromagnético

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

En una región del espacio tenemos un par de campos dados por las expresiones, en coordenadas cilíndricas,

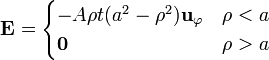
$\mathbf{E}=\begin{cases} -A\rho t(a^2-\rho^2)\mathbf{u}_\varphi & \rho< a \\ \mathbf{0} & \rho > a\end{cases}$ $\mathbf{B}=\begin{cases}At^2(a^2-2\rho^2)\mathbf{u}_z & \rho < a \\ \mathbf{0} & \rho > a\end{cases}$

siendo $A$ una constante.

Compruebe que se trata de un posible campo electromagnético.
Calcule las fuentes de este campo.
Determine las densidades volumétricas de energía eléctrica, magnética, electromagnética y de potencia desarrollada por el campo.
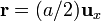Halle la fuerza sobre una carga puntual $\ q$ que en el instante $\ t=a/c$ se encuentra situada en el punto $\mathbf{r}=(a/2)\mathbf{u}_x$ y se mueve con una velocidad 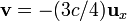$\mathbf{v}=-(3c/4)\mathbf{u}_x$ (siendo $\ c$ la velocidad de la luz).

2 Solución

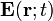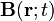En el enunciado se muestran sendas expresiones matemáticas, $\mathbf{E}(\mathbf{r};t)$ y $\mathbf{B}(\mathbf{r};t)$ , funciones de la posición y del tiempo. Y para que estos campos variables se correspondan con un campo electromagnético deben verificar una serie de propiedades, descritas por las ecuaciones de Maxwell. Básicamente, éstas indican cuáles son las fuentes (escalares y vectoriales) de los campos cómo se distribuyen en el espacio. En su versión local, la expresión local de estas ecuaciones es:

$\begin{array}{ccc}\displaystyle \nabla\cdot\mathbf{E}=\frac{1}{\varepsilon_0}\ \rho_e(\mathbf{r};t) & & \nabla\cdot\mathbf{B}=0\\ \\ \displaystyle \nabla\times\mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} & & \displaystyle\nabla\times\mathbf{B}=\mu_0\left[\mathbf{J}(\mathbf{r};t)+\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}\right]\end{array}$

donde $ρ e$ y 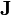$\mathbf{J}$ son, respectivamente, las densidades volumétricas de carga eléctrica y de corriente en el punto del espacio dado por el vector posición $\mathbf{r}$ . Este modelo macroscópico considera a las cargas eléctricas distribuidas en el vacío. En general, el vector 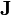$\mathbf{J}$ incluye tanto las corrientes eléctricas causadas por el movimiento de las cargas, como las corrientes equivalentes de imanación, que estarían directamente relacionadas con la distribución (también en el vacío) de dipolos magnéticos. Además, la ley de Ampère-Maxwell establece que la variación en el tiempo del campo eléctrico (corriente de desplazamiento), es también fuente vectorial del campo magnético.

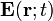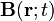Sin embargo, las expresiones anteriores de las ecuaciones de Maxwell sólo describen las distribuciones de fuentes en aquellos puntos del espacio donde los campos $\mathbf{E}(\mathbf{r};t)$ y $\mathbf{B}(\mathbf{r};t)$ son continuos (obsérvese que $\nabla$ es un operador diferencial).

Sea $\ \Sigma$ una superficie que separa dos regiones del espacio y $\mathbf{r}_{{}_\Sigma}$ el vector que indica la posición de un punto arbitrario de dicha superficie. Las ecuaciones de Maxwell en estos puntos se expresan como sigue:

$\begin{array}{ccc}\displaystyle \mathbf{n}\cdot\left[\mathbf{E}(\mathbf{r}_{{}_\Sigma}^+; t)- \mathbf{E}(\mathbf{r}_{{}_\Sigma}^-; t)\right]=\frac{1}{\varepsilon_0}\ \sigma_e(\mathbf{r}{{}_\Sigma};t) & & \mathbf{n}\cdot\left[\mathbf{B}(\mathbf{r}_{{}_\Sigma}^+; t)-\mathbf{B}(\mathbf{r}_{{}_\Sigma}^-; t)\right]=0\\ \\ \displaystyle \mathbf{n}\times\left[\mathbf{E}(\mathbf{r}_{{}_\Sigma}^+; t)- \mathbf{E}(\mathbf{r}_{{}_\Sigma}^-; t)\right]=\mathbf{0} & & \mathbf{n}\times\left[\mathbf{B}(\mathbf{r}_{{}_\Sigma}^+; t)-\mathbf{B}(\mathbf{r}_{{}_\Sigma}^-; t)\right]=\mu_0 \mathbf{K}(\mathbf{r}{{}_\Sigma}^{};t)\end{array}$

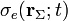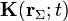donde $\mathbf{n}$ es el vector unitario normal a la superficie en el punto dado por $\mathbf{r}_{{}_\Sigma}$ , y $\sigma_e(\mathbf{r}{{}_\Sigma};t)$ y $\mathbf{K}(\mathbf{r}{{}_\Sigma}^{};t)$ las densidades superficiales de carga eléctrica y de corriente (eléctrica y de imanación) en dicho punto. Como se sabe, estas expresiones indican que la existencia de distribuciones superficiales de fuentes está directamente relacionada con una discontinuidad de las componentes normales del campo eléctrico y de las tangenciales del campo magnético. Por el contrario, las componentes tangenciales de $\mathbf{E}$ y las normales de $\mathbf{B}$ , siempre han de ser continuas.

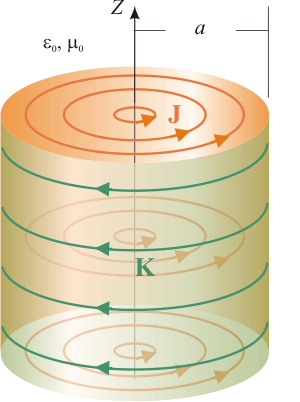
Obsérvese que los campos descritos en el enunciado están definidos en todo el espacio, aunque con expresiones distintas según el punto considerado sea exterior o interior a una superficie cilíndrica de longitud infinita y radio 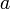$\ a$ . Tomando como el eje de simetría de dicha superficie como eje 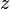$\ z$ , y utilizando las coordenadas cilíndricas para describir el espacio, se tiene que $\ \Sigma: \rho=a$ es una superficie de discontinuidad.

2.1 Verificación de la naturaleza electromagnética de los campos

Para comprobar si los campos variables del enunciado se corresponde con campos electromagnéticos no contamos más que con las propias expresiones de esos campos. Por tanto, no podemos utilizar las ecuaciones relativas a las fuentes escalares de 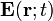$\mathbf{E}(\mathbf{r};t)$ y vectoriales de 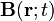$\mathbf{B}(\mathbf{r};t)$ , ya que desconocemos cómo son las distribuciones de carga eléctrica y de corriente. Sin embargo, para que 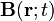$\mathbf{B}(\mathbf{r};t)$ sea un campo magnético es condición necesaria que éste no tenga fuentes escalares en ningún punto del espacio y que sus componente normal a la superficie $\ \Sigma: \rho=a$ sea continua. Además, para que 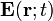$\mathbf{E}(\mathbf{r};t)$ sea un campo eléctrico, sus componentes tangenciales a dicha superficie deben ser continuas, y el rotacional debe coincidir la derivada temporal negativa de 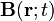$\mathbf{B}(\mathbf{r};t)$ . Procedamos a comprobar estas propiedades.

En el exterior de la superficie cilíndrica (es decir, para $ρ > a$ ) ambos campos son nulos, por tanto, se cumplen las propiedades descritas:

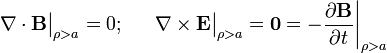
$\begin{array}{ccc}\displaystyle \nabla\cdot\mathbf{B}\big|_{\rho>a}=0;& & \displaystyle \nabla\times\mathbf{E}\big|_{\rho>a}=\mathbf{0}=-\frac{\partial \mathbf{B}}{\partial t}\bigg|_{\rho>a} \end{array}$

Y en el interior del cilindro (región $ρ < a$ )...

$\begin{array}{l}\displaystyle \nabla\cdot\mathbf{B}\big|_{\rho<a}=\frac{\partial}{\partial z}\left[At^2(a^2-2\rho^2)\right]=0\\ \\ \displaystyle \nabla\times\mathbf{E}\big|_{\rho<a}=-2At(a^2-2\rho^2)\mathbf{u}_z=-\frac{\partial \mathbf{B}}{\partial t}\bigg|_{\rho<a}\end{array}$

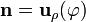... también se verifican dichas propiedades. Sólo queda comprobar la continuidad de las componentes normal de $\mathbf{B}$ y tangencial de $\mathbf{E}$ en la superficie $\ \Sigma: \rho=a$ , donde el vector normal en cada punto es $\mathbf{n}=\mathbf{u}_\rho(\varphi)$ .

El campo $\mathbf{B}$ en el interior del cilindro sólo tiene componente en la dirección de $\mathbf{u}_z$ , que es tangencial a la superficie cilíndrica, luego la componente normal a ambos lados de ésta es nula y, en consecuencia continua:

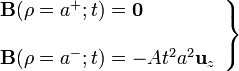
$\left.\begin{array}{l}\mathbf{B}(\rho=a^+; t)=\mathbf{0}\\ \\ \mathbf{B}(\rho=a^-; t)=-At^2a^2\mathbf{u}_z\end{array}\right\}$ $\Rightarrow$ $\mathbf{n}\cdot\left[\mathbf{B}(\rho=a^+; t)-\mathbf{B}(\rho=a^-; t)\right]=-\mathbf{u}_\rho\cdot\mathbf{B}(\rho=a^-; t)=0$

Por su parte, el campo eléctrico dentro del cilindro se anula en la superficie interior de éste (en $ρ = a -$ ), luego la continuidad se verifica para todas las componentes y,en particular, para las tangenciales:

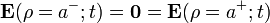
$\mathbf{E}(\rho=a^-; t)=\mathbf{0}=\mathbf{E}(\rho=a^+; t)$ $\Rightarrow$ $\mathbf{n}\times\left[\mathbf{E}(\rho=a^+; t)-\mathbf{E}(\rho=a^-; t)\right]=\mathbf{u}_\rho\times\mathbf{0}=\mathbf{0}$

En conclusión, los campos propuestos en el enunciado cumplen las condiciones necesarias para ser campos electromagnéticos.

2.2 Fuentes de los campos

...Y asumiendo que los son, obtengamos las distribuciones de carga eléctrica y de corrientes los crean. Para ello, calcularemos la divergencia de $\mathbf{E}$ y el salto de su componente normal en la superficie de discontinuidad, y el rotacional de $\mathbf{B}$ y la discontinuidad de sus componentes tangenciales.

En la región exterior ( $ρ > a$ ) donde los campos son nulos, sus correspondientes divergencia, rotacional y derivadas temporales serán nulas. Por tanto, en esta región no hay fuentes de ningún tipo.

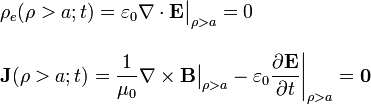
$\begin{array}{l}\displaystyle \rho_e(\rho>a;t)=\varepsilon_0\nabla\cdot\mathbf{E}\big|_{\rho>a}=0\\ \\ \displaystyle\mathbf{J}(\rho>a;t)=\frac{1}{\mu_0}\nabla\times\mathbf{B}\big|_{\rho>a}-\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}\bigg|_{\rho>a}=\mathbf{0}\end{array}$

En el interior ( $ρ < a$ ), la divergencia del campo eléctrico es también nula por lo que tampoco va a haber carga eléctrica neta distribuida en volumen:

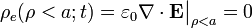
$\nabla\cdot\mathbf{E}\big|_{\rho<a}=-\frac{\varepsilon_0}{\rho}\frac{\partial}{\partial \varphi}\big[A\rho t(a^2-\rho^2)\big]=0$ $\Rightarrow$ $\displaystyle \rho_e(\rho<a;t)=\varepsilon_0\nabla\cdot\mathbf{E}\big|_{\rho<a}=0$

Tampoco va a haber cantidades netas de carga eléctrica distribuidas en $\ \Sigma: \rho=a$ ya que, como vimos en el apartado anterior, todas las componentes del campo eléctrico presentan continuidad, pues éste se anula en interior de la superficie:

$\displaystyle \sigma_e(\rho=a;t)=\varepsilon_0\, \mathbf{n}\cdot\left[\mathbf{E}(\rho=a^+; t)-\mathbf{E}(\rho=a^-; t)\right]=\varepsilon_0\,\mathbf{u}_\rho\cdot\mathbf{0}=0$

Es decir, el campo eléctrico del ejercicio sólo tiene fuentes vectoriales. Es decir, este campo no es creado por cargas eléctricas, sino por la variación en el tiempo del campo magnético, tal como se comprobó en el apartado anterior. Calculemos las corrientes que crean dicho campo 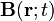$\mathbf{B}(\mathbf{r};t)$ . En el interior de la superficie cilíndrica ( $ρ < a$ ) se obtiene una distribución volúmetrica:

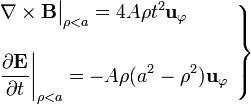
$\left.\begin{array}{l}\displaystyle\nabla\times\mathbf{B}\big|_{\rho<a}=4A\rho t^2\mathbf{u}_\varphi\\ \\ \displaystyle\frac{\partial \mathbf{E}}{\partial t}\bigg|_{\rho<a}=-A\rho(a^2-\rho^2)\mathbf{u}_\varphi\end{array}\right\}$ $\Rightarrow$ $\displaystyle \mathbf{J}(\rho<a;t)=\frac{1}{\mu_0}\nabla\times\mathbf{B}\big|_{\rho<a}-\varepsilon_0\frac{\partial \mathbf{E}}{\partial t}\bigg|_{\rho<a}=\frac{A\rho}{\mu_0}\left[4 t^2+\mu_0\varepsilon_0(a^2-\rho^2)\right]\mathbf{u}_\varphi$

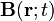En $\ \Sigma: \rho=a$ se obtiene una distribución superficial ligada a la discontinuidad que sufren las componentes tangenciales de $\mathbf{B}(\mathbf{r};t)$ , como se vio en el apartado anterior:

$\displaystyle \mathbf{K}(\rho=a;t)=\frac{1}{\mu_0}\mathbf{n}\times\left[\mathbf{B}(\rho=a^+; t)-\mathbf{B}(\rho=a^-; t)\right]=-\frac{1}{\mu_0}\mathbf{u}_\rho\times\mathbf{B}(\rho=a^-; t)=-\frac{At^2a^2}{\mu_0} \mathbf{u}_\varphi$

2.3 Densidades de energía y de potencia desarrollada

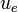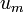Considerando que los campos en el enunciado y las corrientes que los crean se distribuyen en el espacio vacío, las densidades volumétricas de energía eléctrica y magnética ( $\ u_e$ y $\ u_m$ , respectivamente), son:

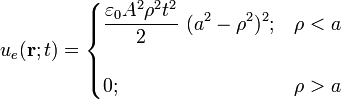
$\frac{\mathrm{d}U_e}{\mathrm{d}\tau}=u_e(\mathbf{r};t)=\frac{\varepsilon_0}{2} |\mathbf{E}(\mathbf{r};t)|^2=$ $\Rightarrow$ $u_e(\mathbf{r};t)=\begin{cases}\displaystyle \frac{\varepsilon_0A^2\rho^2t^2}{2}\ (a^2-\rho^2)^2; & \rho<a \\ \\ \displaystyle 0; &\rho>a\end{cases}$

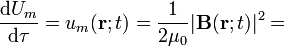
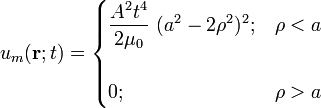
$\frac{\mathrm{d}U_m}{\mathrm{d}\tau}=u_m(\mathbf{r};t)=\frac{1}{2\mu_0} |\mathbf{B}(\mathbf{r};t)|^2=$ $\Rightarrow$ $u_m(\mathbf{r};t)=\begin{cases}\displaystyle \frac{A^2t^4}{2\mu_0}\ (a^2-2\rho^2)^2; & \rho<a \\ \\ \displaystyle 0; &\rho>a\end{cases}$

La densidad de energía electromagnética en cada punto del espacio y en cada instante de tiempo, 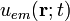$\ u_{em}(\mathbf{r};t)$ , se define como la suma de las anteriores densidades de energía:

$\frac{\mathrm{d}U_{em}}{\mathrm{d}\tau}=u_{em}(\mathbf{r};t)=\frac{1}{2} \left\{\varepsilon_0|\mathbf{E}(\mathbf{r};t)|^2+\frac{|\mathbf{B}(\mathbf{r};t)|^2}{\mu_0}\right\}$ $\Rightarrow$ $u_{em}(\mathbf{r};t)=u_{e}(\mathbf{r};t)+u_{m}(\mathbf{r};t)$

Por su parte, la potencia desarrollada por el campo es el trabajo que por unidad de tiempo realiza el campo electromagnético para mover una carga puntual. Recordemos brevemente este concepto: sea una carga casi puntual 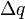$\ \Delta q$ situada en un punto arbitrario cuya posición viene dada por el radio vector 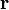$\ \mathbf{r}$ y donde existe el campo electromagnético 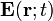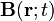$\mathbf{E}(\mathbf{r};t)$ , $\mathbf{B}(\mathbf{r};t)$ . 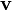La potencia instantánea desarrollada por la fuerza de Lorentz sobre esta carga cuando se mueve con velocidad $\ \mathbf{v}$ , es:

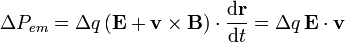
$\Delta P_{em}=\Delta q\left(\mathbf{E}+\mathbf{v}\times\mathbf{B}\right)\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}=\Delta q\, \mathbf{E}\cdot\mathbf{v}$

Esta potencia depende de la cantidad de carga que haya en el punto; pero si calculamos la densidad de potencia electromangética desarrollada (es decir, por unidad de volumen), tendremos...

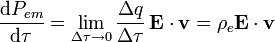
$\frac{\mathrm{d}P_{em}}{\mathrm{d}\tau}=\lim_{\Delta \tau\rightarrow 0}\frac{\Delta q}{\Delta \tau}\, \mathbf{E}\cdot\mathbf{v}=\rho_e \mathbf{E}\cdot\mathbf{v}$

Obsérvese que en esta expresión sólo van a contribuir aquellas cargas eléctricas que se mueve, pues sólo éstas implican que los campos electromagnéticos realicen trabajo. En consecuencia, se tendrá que el productor de la densidad de carga neta móvil por la velocidad que tienen las cargas en ese punto es, por definición la densidad volumétrica de corriente eléctrica:

$\frac{\mathrm{d}P_{em}}{\mathrm{d}\tau}=\rho_e \mathbf{E}\cdot\mathbf{v}=\mathbf{E}\cdot\mathbf{J}_\mathrm{elec}$

Anteriormente calculamos la densidad volumétrica de corriente que actúa como fuente vectorial del campo magnético. En principio, ésta podría estar motivada tanto por un movimimiento de cargas eléctricas, como por una imanación no uniforme del medio material (existencia de dipolos magnéticos). Pero consideremos que en nuestro sistema no hay medios materiales: sólo cargas eléctricas moviéndose en el vacío. Entonces, 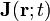$\mathbf{J}(\mathbf{r};t)$ del apartado anterior es corriente eléctrica. En consecuencia, la densidad de potencia electromagnética desarrollada por los campos del ejercicio es:

$\frac{\mathrm{d}P_{em}}{\mathrm{d}\tau}\bigg|_{\rho<a}=\mathbf{E}(\rho<a;t)\cdot\mathbf{J}(\rho<a;t)=-\frac{A^2\rho^2 t}{\mu_0}(a^2-\rho^2)\left[4 t^2+\mu_0\varepsilon_0(a^2-\rho^2)\right]$

Obviamente, en la región exterior a la superifice cilíndrica la densidad de potencia electromagnética es nula, ya que no hay ni campo eléctrico ni corrientes.

Estos mismos resultados puede obtenerse mediante un procedimiento alternativo, consistente en evaluar el teorema de Poynting en cada punto del espacio:

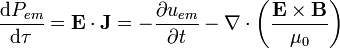
$\frac{\mathrm{d}P_{em}}{\mathrm{d}\tau}=\mathbf{E}\cdot\mathbf{J}=-\frac{\partial u_{em}}{\partial t}-\nabla\cdot\left(\frac{\mathbf{E}\times\mathbf{B}}{\mu_0}\right)$

2.4 Fuerza sobre una carga puntual

La fuerza que actúa sobre una carga puntual $\ q$ viene dada por la ley de Lorentz:

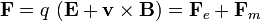
$\mathbf{F}= q\, \left(\mathbf{E}+\mathbf{v}\times\mathbf{B}\right)=\mathbf{F}_e+\mathbf{F}_m$

Calculemos el valor de los dos términos de esta expresión en la posición ocupada por la partícula en el instante considerado, 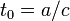$\ t_0=a/c$ (donde $c=1/\sqrt{\mu_0\varepsilon_0}$ es la velocidad de la luz en el vacío), y con la velocidad descrita en el enunciado.

La posición de la partícula viene dada por el radio vector expresado en cartesianas 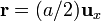$\mathbf{r}=(a/2)\mathbf{u}_x$ , que en cilíndricas se corresponde por el punto de coordenadas 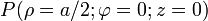$\ P(\rho=a/2;\varphi=0;z=0)$ . Este punto es interior a la superficie cilíndrica $\ \Sigma:\rho=a$ , donde tanto el campo eléctrico como el magnético son no nulos. Por tanto, sobre la partícula actuará tanto una fuerza eléctrica como magnética:

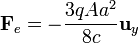
$\mathbf{F}_e= q\, \mathbf{E}(P;t_0)=-q\,A\frac{a}{2}\frac{a}{c}\left[a^2-\left(\frac{a}{2}\right)^2\right]\mathbf{u}_\varphi(0)$ $\Rightarrow$ $\mathbf{F}_e=-\frac{3qAa^2}{8c}\mathbf{u}_y$

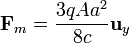
$\mathbf{F}_m=q\,\mathbf{v}(P;t_0)\times \mathbf{B}(P;t_0)=-q\, A\frac{3c}{4}\left(\frac{a}{c}\right)^2\left[a^2-2\left(\frac{a}{2}\right)^2\right]\left(\mathbf{u}_x\times\mathbf{u}_z\right)$ $\Rightarrow$ $\mathbf{F}_m=\frac{3qAa^2}{8c}\mathbf{u}_y$

Es decir, las fuerzas eléctrica y magnética que actúan sobre la carga en movimiento son opuestas. En consecuencia, la fuerza total es nula:

$\mathbf{F}(P;t_0)=\mathbf{F}_e(P;t_0)+\mathbf{F}_m(P;t_0)=\mathbf{0}$

Fuentes y fuerza de un posible campo electromagnético

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Verificación de la naturaleza electromagnética de los campos

2.2 Fuentes de los campos

2.3 Densidades de energía y de potencia desarrollada

2.4 Fuerza sobre una carga puntual

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES