Problemas del primer principio de la termodinámica (GIE)

De Laplace

Revisión a fecha de 11:09 22 feb 2014; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Trabajo en una compresión por un peso
2 Calor en una expansión isoterma por un peso
3 Sucesión de tres procesos cuasiestáticos
4 Mezcla de dos cantidades de agua
5 Mezcla de agua y hielo
6 Calor necesario para evaporar hielo
7 Mezcla de hielo y vapor de agua
8 Trabajo en fusión de hielo
9 Calentamiento de un gas a volumen y a presión constante
10 Calentamiento de agua con una resistencia
11 Compresión lineal de un gas
12 Expansión lineal de un gas
13 Termómetro de gas
14 Calor que escapa por una ventana
15 Calor que escapa del cuerpo humano
16 Congelamiento gradual de un estanque
17 Trabajo en un gas con resorte
18 Fusión de un trozo de hielo

1 Trabajo en una compresión por un peso

Un tubo vertical de sección cuadrada de 4.0 cm de lado contiene hidrógeno a 27°C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0\,cm de altura.

Suponiendo que las paredes del tubo son diatermas, calcule el trabajo realizado sobre el sistema entre el estado inicial y el estado de equilibrio final sí…
1. Se coloca bruscamente sobre la tapa una pesa de 4.0 kg.
2. Se colocan sobre el émbolo 4.0 kg de arena grano a grano.
Para los dos casos anteriores, halle la variación en la energía interna del gas y el calor que entra en el sistema durante el proceso.
Suponga ahora que las paredes del tubo son adiabáticas. ¿Cómo quedan en ese caso el trabajo, el calor y la variación de la energía interna para los dos procesos considerados?

2 Calor en una expansión isoterma por un peso

Se tiene una balanza formada por un recipiente cilíndrico de 16 cm² de sección lleno de aire (considerado como un gas ideal). El tubo está cerrado herméticamente en su parte inferior por un émbolo que puede deslizarse sin rozamiento y que tiene un gancho en su cara inferior. Las paredes y el émbolo no están aislados térmicamente. Inicialmente el émbolo se encuentra a 15 cm de la pared superior, y el gas en equilibrio mecánico y térmico con el exterior, que se halla a 1 bar y 300 K. Se cuelga bruscamente del pistón un saco de harina de 4 kg.

¿Cuánto desciende aproximadamente el pistón hasta que se alcanza de nuevo el equilibrio?
¿Cuánto vale aproximadamente el calor que entra en el sistema en este proceso?
Suponga que el saco tiene un agujero, de forma que la harina se escapa lentamente hasta vaciarse por completo (despreciamos el peso del propio saco). ¿Cuánto vale el calor que entra en el sistema en este segundo proceso?

Datos: Constante de los gases ideales: 8.314 J/K·mol; Razón de capacidades caloríficas del aire: 1.4.

3 Sucesión de tres procesos cuasiestáticos

Un cilindro de 20 cm de diámetro contiene aire y está cerrado por un émbolo. Inicialmente el aire tiene una temperatura de 27 °C y una presión de 100 kPa, que también es la presión exterior, estando el émbolo a 10 cm del fondo. Entonces se realiza el siguiente proceso cuasiestático

I: Se atornilla el émbolo y se calienta el aire hasta 327 °C, sumergiéndolo en un baño a esta temperatura.

II: Se libera el émbolo lentamente, dejando que se expanda el aire hasta que su presión vuelve a ser la inicial. En este proceso el aire se mantiene a la temperatura de 327 °C.

III: Con el émbolo libre, se enfría gradualmente hasta que la temperatura vuelve a ser la inicial.

Para este proceso:

Halle la presión, volumen y temperatura al final de cada fase del proceso.
Calcule el trabajo en cada fase, así como el trabajo neto total.
Calcule la variación en la energía interna y el calor en cada paso y su variación neta.

4 Mezcla de dos cantidades de agua

En un recipiente adiabático se ponen en contacto 750 cm³ de agua a 20°C con 250 cm³ de agua a 80°C, siendo la temperatura exterior de 50°C. ¿Cuál es la temperatura final de la mezcla? ¿Cuánto calor entra en cada subsistema?

¿Cómo cambian los resultados si las paredes son diatermas?

5 Mezcla de agua y hielo

Dentro de un recipiente adiabático se sumerge un bloque de 100 g de hielo a 0.0 °C en 1.0 litros de agua a 20 °C. Determine si se funde todo el hielo y la temperatura final del sistema. ¿Qué ocurre si en lugar de 100 g se tiene 1.0 kg de hielo?

6 Calor necesario para evaporar hielo

Calcule la cantidad de calor necesaria para llevar un bloque de hielo de 500 g inicialmente a −10 °C hasta el estado de vapor de agua a 115 °C, manteniéndose la presión constante en 101.3 kPa.

7 Mezcla de hielo y vapor de agua

En un recipiente a presión constante de 101.3 kPa, se ponen en contacto 1.0 m³ de vapor de agua a 115 °C con 500 g de hielo a −10 °C. Determine la temperatura final del sistema.

Dato: La constante específica de los gases ideales para el vapor de agua vale 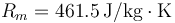$R_m = 461.5\,\mathrm{J}/\mathrm{kg}\cdot\mathrm{K}$

8 Trabajo en fusión de hielo

Tenemos 1 kg de hielo (densidad de masa 917 kg/m³) a 0 °C, al cual se le cede lentamente calor a una presión de 101.3 kPa hasta que convierte por completo en agua (densidad de masa 1000 kg/m³). Para este proceso, halle

El calor que entra en el sistema
El trabajo realizado sobre el sistema
La variación de entalpía y de energía interna del sistema

9 Calentamiento de un gas a volumen y a presión constante

Un cilindro de 10 cm de diámetro está cerrado por un émbolo. La presión exterior es en todo momento de 100 kPa. La cámara está llena de aire que se encuentra inicialmente a 300 K y el émbolo está a una distancia de 10 cm respecto del fondo. Se calienta cuasiestáticamente el gas hasta que su temperatura llega a 450 K. Calcule el calor que entra el gas, el trabajo que se realiza sobre él, así como la variación de su energía interna y de su entalpía:

Si el émbolo está bloqueado de forma que no puede desplazarse.
Si el émbolo está libre y puede deslizarse sin rozamiento por el tubo.

10 Calentamiento de agua con una resistencia

En una cámara con un émbolo móvil se coloca 500 cm³ de agua a 300 K. El exterior se encuentra a una presión de 100 kPa. Se le comunica lentamente calor al agua hasta que se evapora por completo.

Calcule el calor necesario para que se realice este proceso.
Halle el trabajo que se realiza sobre el agua.
Calcule la variación en la entalpía y en la energía interna del agua.
Suponga que el calentamiento se produce mediante una resistencia eléctrica a una tensión de 220 V por la que pasa una corriente de 2 A. ¿Cuánto tiempo tarda en realizarse el proceso? En este caso, la energía entra en el sistema en forma de calor o de trabajo?

11 Compresión lineal de un gas

Se tiene un volumen $V 0$ de un gas ideal diatómico a una presión $p 0$ y una temperatura $T 0$ encerrado en un recipiente con un pistón móvil. Este gas se comprime reversiblemente según la ley

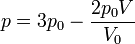
$p = 3p_0-\frac{2p_0V}{V_0}$

reduciéndose el volumen hasta $V 0 / 2$ .

Trace la gráfica del proceso en un diagrama pV.
Calcule la temperatura final del proceso.
Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
¿Para qué volumen durante el proceso la temperatura es máxima? Halle el valor de esta temperatura máxima.
Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle $W$ , $Δ U$ y $Q$ en cada uno de los dos subprocesos.

12 Expansión lineal de un gas

Se tiene una cantidad fija de un gas ideal diatómico situada a una presión $p 0$ , volumen $V 0$ y temperatura $T 0$ . Experimenta un proceso tal que la presión final es $2 p 0$ y el volumen $2 V 0$ .

En este proceso, ¿cómo varía la temperatura?
Halle el incremento de la energía interna en este proceso

Supongamos que el proceso anterior ocurre de manera cuasiestática según la ley

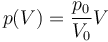
$p(V) = \frac{p_0}{V_0}V$

¿Cuánto trabajo se realiza sobre el gas en esta expansión cuasiestática?
¿Cuánto calor entra en el gas en la expansión cuasiestática?

13 Termómetro de gas

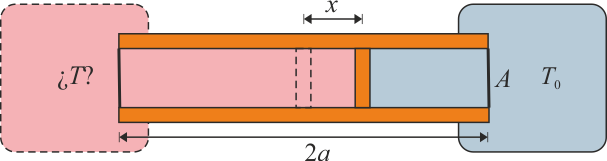
Se construye un termómetro de gas ideal según el siguiente principio: un tubo cilíndrico de sección $S$ y longitud $2 a$ con paredes adiabáticas y bases diatermas es dividido por un pistón, también adiabático, que puede deslizarse sin rozamiento por el interior del tubo. En el interior de las dos cámaras se encuentra un gas ideal. Una de las dos cámaras se mantiene en contacto térmico con un foco a temperatura $T 0$ , mientras que la otra se pone en contacto con el sistema cuya temperatura se quiere medir. Cuando las dos temperaturas son iguales el pistón se encuentra en la posición central y la presión del gas es $p 0$ .

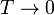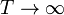Calcule la temperatura absoluta $T$ a la que se encuentra el sistema cuando el pistón se ha desplazado una cantidad $x$ desde el centro hacia el sistema a $T 0$ . ¿Resulta una escala lineal de temperaturas? ¿A cuánto tiende $x$ si $T\to 0$ o si $T\to\infty$ ?
Supongamos que se parte del equilibrio a $T 0$ y que la variación de la temperatura del gas de la cámara exterior y el desplazamiento del pistón en $x$ ha sido de forma cuasiestática y reversible. ¿Cuáles son los calores, trabajos e incrementos de energía interna para cada una de las cámaras y para el tubo completo, como función del desplazamiento $x$ del pistón?
Supongamos que el tubo mide 20 cm, la temperatura de referencia es $T_0 = 300^\circ\mathrm{K}$ y el pistón se desplaza 1 cm. ¿Cuál es la temperatura del sistema exterior?
Si además sabemos que la sección del tubo es de 10 cm², el gas contenido es aire y la presión inicial es 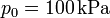$p_0 = 100\,\mathrm{kPa}$ , ¿cuánto valen los calores, trabajos e incrementos de energía interna del segundo apartado?

14 Calor que escapa por una ventana

En una habitación que se encuentra a una temperatura de 22 °C se encuentra una ventana de 1.60 m por 1.20 m. con un vidrio de 5 mm de espesor. El exterior de la habitación se halla a 10 °C. Determine aproximadamente la cantidad de calor que escapa de la habitación por segundo. La conductividad térmica del vidrio es de 0.96 W/m·K.

Suponga ahora que delante de la ventana se colocan unos finos visillos de espesor despreciable, estando los visillos a 2 cm de la ventana. ¿Cuál es entonces la cantidad de calor que escapa de la ventana por segundo? La conductividad térmica del aire vale 0.024 W/m·K

15 Calor que escapa del cuerpo humano

Determine la cantidad de calor que escapa por cm² de piel del cuerpo humano si la piel se encuentra a 33 °C y el aire exterior se encuentra a 15 °C, estando el cuerpo cubierto por una sábana de algodón de 1 mm de espesor. ¿Y si además de la sábana está tapado con una manta de lana de 5 mm de espesor? La conductividad térmica de la lana es 0.03 W/m·K y la del algodón 0.04 W/m·K.

16 Congelamiento gradual de un estanque

Un estanque de agua a 0 °C está cubierto por una capa de hielo de 4.00 cm de espesor. Si la temperatura del aire permanece constante a -10.0 °C, ¿cuánto tardará el espesor de la capa de hielo en alcanzar los 8.00 cm?

La conductividad térmica del hielo es 2.22 W/m·K y la entalpía de fusión del agua vale 334 kJ/kg.

17 Trabajo en un gas con resorte

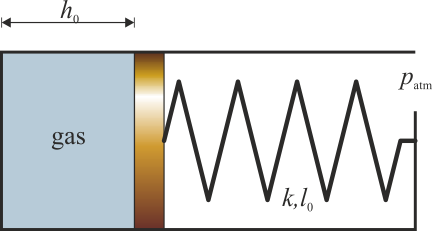
Se tiene un cilindro de sección $S$ en el interior del cual hay un pistón que puede deslizarse sin rozamiento. El pistón cierra una cámara en la que hay un gas ideal. La cara exterior del pistón está unida al extremo del tubo mediante un resorte de constante $k$ y longitud natural $l 0$ . Esta parte del tubo está abierta a la atmósfera. Para un cierto valor de la temperatura, $T 0$ , la presión es la atmosférica, el pistón se encuentra a una distancia $h 0$ del fondo y el resorte no ejerce fuerza alguna. Cuando el gas se calienta, se expande y el resorte se comprime.

Halle el trabajo realizado sobre el gas cuando su temperatura pasa de $T 0$ a $T 1$ .
Calcule la variación de la energía interna del gas y el calor transferido al gas en el proceso.
Calcule el trabajo, la variación en la energía total y el calor, si consideramos que el sistema esta formado por el gas y el muelle.

18 Fusión de un trozo de hielo

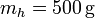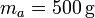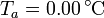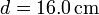Se tiene un bloque de hielo de masa $m_h = 500\,\mathrm{g}$ sumergido en un volumen de agua de masa $m_a = 500\,\mathrm{g}$ , ambos a una temperatura $T_a = 0.00\,^\circ\mathrm{C}$ . El conjunto está contenido en un recipiente cilíndrico de vidrio, de diámetro $d = 16.0\,\mathrm{cm}$ y espesor 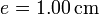$e = 1.00\,\mathrm{cm}$ , abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). 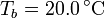El recipiente está sumergido en un baño de agua a $T_b = 20.0\,^\circ \mathrm{C}$ .

Calcule la superficie de agua en contacto con el recipiente y la cantidad de calor que entra en él en 1.00 s.
Halle la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará aproximadamente en derretirse por completo?

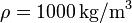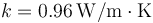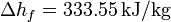Datos: Densidad de masa del agua líquida $\rho = 1000\,\mathrm{kg}/\mathrm{m}^3$ ; Conductividad térmica del vidrio $k= 0.96\,\mathrm{W}/\mathrm{m}\cdot\mathrm{K}$ ; Entalpía específica de fusión: $\Delta h_f= 333.55\,\mathrm{kJ}/\mathrm{kg}$ .