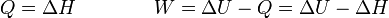Calentamiento de un gas a volumen y a presión constante

De Laplace

Contenido

1 Enunciado
2 A volumen constante
3 A presión constante
4 Conclusión

1 Enunciado

Un cilindro de 10 cm de diámetro está cerrado por un émbolo. La presión exterior es en todo momento de 100 kPa. La cámara está llena de aire que se encuentra inicialmente a 300 K y el émbolo está a una distancia de 10 cm respecto del fondo. Se calienta cuasiestáticamente el gas hasta que su temperatura llega a 450 K. Calcule el calor que entra el gas, el trabajo que se realiza sobre él, así como la variación de su energía interna y de su entalpía:

Si el émbolo está bloqueado de forma que no puede desplazarse.
Si el émbolo está libre y puede deslizarse sin rozamiento por el tubo.

2 A volumen constante

El aire puede considerarse un gas diatómico cuya capacidad calorífica molar vale

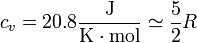
$c_v = 20.8\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}} \simeq \frac{5}{2}R$

2.1 Calor

En el caso de un calentamiento a volumen constante, la cantidad de calor que entra en el gas vale

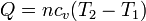
$Q = nc_v(T_2-T_1)\,$

donde el número de moles lo obtenemos de los datos del estado inicial. Tenemos que

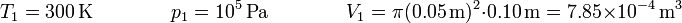
$T_1 = 300\,\mathrm{K}\qquad\qquad p_1 = 10^5\,\mathrm{Pa}\qquad\qquad V_1 = \pi (0.05\,\mathrm{m})^2\cdot 0.10\,\mathrm{m}=7.85\times 10^{-4}\,\mathrm{m}^3$

y sustituyendo

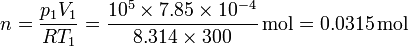
$n = \frac{p_1 V_1}{R T_1} = \frac{10^5\times 7.85\times 10^{-4} }{8.314\times 300}\,\mathrm{mol} = 0.0315\,\mathrm{mol}$

Esto nos da el calor

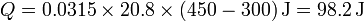
$Q = 0.0315\times 20.8\times(450-300)\,\mathrm{J}=98.2\,\mathrm{J}$

2.2 Trabajo

En un proceso a volumen constante no se realiza trabajo sobre el gas

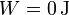
$W = 0\,\mathrm{J}$

2.3 Energía interna

Por el primer principio de la termodinámica

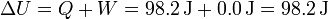
$\Delta U = Q + W = 98.2\,\mathrm{J}+0.0\,\mathrm{J} = 98.2\,\mathrm{J}$

Este resultado se podría haber hallado directamente aplicando que la energía interna es una función de estado y su incremento vale (suponiendo $c v$ constante)

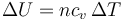
$\Delta U = nc_v\,\Delta T$

independientemente de si el proceso es a presión constante, a volumen constante o de cualquier otra forma.

2.4 Entalpía

La entalpía de un gas se define como

$H = U + p V\,$

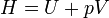
con lo que su incremento vale

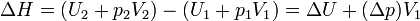
$\Delta H = (U_2+p_2V_2)-(U_1+p_1V_1) = \Delta U + (\Delta p)V_1\,$

donde hemos usado que el volumen final es igual al inicial. El incremento en la presión del gas se debe al aumento de temperatura

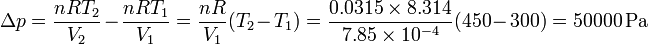
$\Delta p = \frac{nRT_2}{V_2}-\frac{nRT_1}{V_1}=\frac{nR}{V_1}(T_2-T_1) = \frac{0.0315\times 8.314}{7.85\times 10^{-4}}(450-300)=50000\,\mathrm{Pa}$

y esto nos da una variación de la entalpía

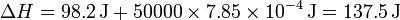
$\Delta H = 98.2\,\mathrm{J}+50000\times 7.85\times 10^{-4}\,\mathrm{J} = 137.5\,\mathrm{J}$

Se pueden ahorrar muchas cuentas si en lugar de sustituir directamente los valores numéricos se opera algebraicamente. Tenemos

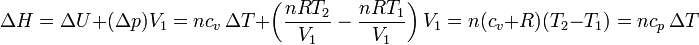
$\Delta H = \Delta U + (\Delta p)V_1 = nc_v\,\Delta T + \left(\frac{nRT_2}{V_1}-\frac{nRT_1}{V_1}\right)V_1 = n(c_v+R)(T_2-T_1) = n c_p\,\Delta T$

siendo $c p$ la capacidad calorífica molar a presión constante, que para un gas diatómico como el aire vale

$c_p = 29.1\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\simeq \frac{7}{2}R$

Este resultado es general. Para un gas ideal la variación de entalpía, que es una una función de estado, vale (suponiendo $c p$ constante)

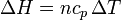
$\Delta H = nc_p\,\Delta T$

independientemente de si el proceso es a presión constante, a volumen constante o de cualquier otra forma.

3 A presión constante

3.1 Calor

En el segundo caso, el pistón se va desplazando de forma que en todo momento hay equilibrio mecánico entre el gasy el exterior, por lo que la presión interior permance constante en 100 kPa. En este caso, el calor suministrado al gas vale

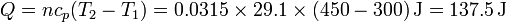
$Q = nc_p(T_2-T_1) = 0.0315\times 29.1\times(450-300)\,\mathrm{J} = 137.5\,\mathrm{J}$

Vemos que el calor es superior al calculado anteriormente e igual a la variación de entalpía que hallamos antes.

3.2 Trabajo

En este caso sí se realiza trabajo sobre el gas ya que éste se expande. Este trabajo será negativo y se calcula como

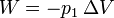
$W = -p_1\,\Delta V$

donde el incremento de volumen es igual a

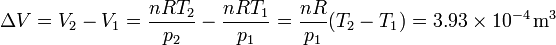
$\Delta V = V_2 - V_1 = \frac{nRT_2}{p_2}-\frac{nRT_1}{p_1}=\frac{nR}{p_1}(T_2-T_1) = 3.93\times 10^{-4}\,\mathrm{m}^3$

La altura a la que sube el pistón es

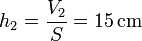
$h_2 = \frac{V_2}{S} = 15\,\mathrm{cm}$

tal como nos predice la ley de Charles, ya que la temperatura se ha incrementado en un 50%. El trabajo vale entonces

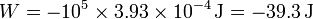
$W = -10^5\times 3.93\times 10^{-4}\,\mathrm{J} = -39.3\,\mathrm{J}$

3.3 Entalpía

En un proceso a presión constante, el calor que entra en el sistema es igual a la variación de la entalpía, por lo que

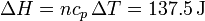
$\Delta H = nc_p\,\Delta T = 137.5\,\mathrm{J}$

Este es el mismo resultado que en el caso a volumen constante. La razón es que la entalpía es una función de estado que para un gas ideal solo depende de la temperatura del gas. El incremento de temperatura es el mismo en los dos procesos.

3.4 Energía interna

La energía interna la podemos hallar a partir del calor y el trabajo, que ya conocemos

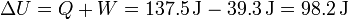
$\Delta U = Q + W = 137.5\,\mathrm{J}-39.3\,\mathrm{J}=98.2\,\mathrm{J}$

o directamente a partir de la variación en la temperatura

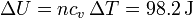
$\Delta U = nc_v\,\Delta T = 98.2\,\mathrm{J}$

4 Conclusión

Comparando los dos procesos, vemos que:

El calor que entra en el sistema para conseguir un aumento de temperatura dado es mayor en un proceso a presión constante. La razón es que no todo este calor se queda en el sistema sino que parte se emplea en realizar el trabajo de expansión del gasa.
La variación de la energía interna y de la entalpía es la misma en ambos procesos, ya que sus incrementos solo dependen del aumento de temperaturas, que es el mismo en los dos casos.
El problema se podría haber resuelto calculando previamente las variaciones en la energían interna y la entalpía

$\Delta U = nc_v\,\Delta T\qquad\qquad \Delta H = nc_p\,\Delta T$

y luego hallando el calor y el trabajo

A volumen constante

$W=0\qquad\qquad Q = \Delta U$

A presión constante

$Q=\Delta H\qquad\qquad W =\Delta U - Q = \Delta U - \Delta H$

Calentamiento de un gas a volumen y a presión constante

De Laplace

Contenido

1 Enunciado

2 A volumen constante

2.1 Calor

2.2 Trabajo

2.3 Energía interna

2.4 Entalpía

3 A presión constante

3.1 Calor

3.2 Trabajo

3.3 Entalpía

3.4 Energía interna

4 Conclusión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES