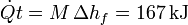Fusión de un trozo de hielo

De Laplace

Contenido

1 Enunciado
2 Flujo de calor
3 Fusión del hielo
- 3.1 Hielo fundido por segundo
- 3.2 Tiempo total de fusión

1 Enunciado

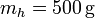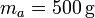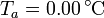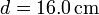Se tiene un bloque de hielo de masa $m_h = 500\,\mathrm{g}$ sumergido en un volumen de agua de masa $m_a = 500\,\mathrm{g}$ , ambos a una temperatura $T_a = 0.00\,^\circ\mathrm{C}$ . El conjunto está contenido en un recipiente cilíndrico de vidrio, de diámetro $d = 16.0\,\mathrm{cm}$ y espesor 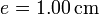$e = 1.00\,\mathrm{cm}$ , abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). 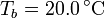El recipiente está sumergido en un baño de agua a $T_b = 20.0\,^\circ \mathrm{C}$ .

Calcule la superficie de agua en contacto con el recipiente y la cantidad de calor que entra en él en 1.00 s.
Halle la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará aproximadamente en derretirse por completo?

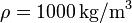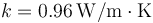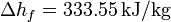Datos: Densidad de masa del agua líquida $\rho = 1000\,\mathrm{kg}/\mathrm{m}^3$ ; Conductividad térmica del vidrio $k= 0.96\,\mathrm{W}/\mathrm{m}\cdot\mathrm{K}$ ; Entalpía específica de fusión: $\Delta h_f= 333.55\,\mathrm{kJ}/\mathrm{kg}$ .

2 Flujo de calor

2.1 Altura del agua

La altura a la que llega el agua la obtenemos por simple aplicación del principio de Arquímedes. Tenemos 500 g de agua, que ocupan 500 cm³, y 500 g de hielo.

Este trozo de hielo desaloja una cantidad de agua que pesa 500 g (pues el hielo está en equilibrio y su peso se compensa por el empuje del agua). El volumen correspondiente al agua desalojada será por tanto 500 cm³ y el volumen total de agua más volumen desalojado es

500 cm³ + 500 cm³ = 1000 cm³

A medida que el hielo se derrita, ¿el nivel de agua subirá o bajará? Ninguna de las dos cosas.

Supongamos que se ha derretido parcialmente y en un momento dado quedan 200 g de hielo. Los 300 g restantes se habrán convertido en agua, con lo que ahora tendremos 800 g de agua. Por su parte, los 200 g de hielo restante desalojan 200 g de agua, que ocupan 200 cm³, con lo que el volumen total es

800 cm³ + 200 cm³ = 1000 cm³

Obviamente, cuando el hielo se funda por completo, tendremos 1000 g de agua que ocupan 1000 cm³.

En resumen,

El nivel del agua con hielo flotando no cambia cuando el hielo se derrite y es igual al que habría si toda el agua fuera líquida.

Si tenemos que el agua ocupa un volumen de 1000 cm³ la altura a la que llega la obtenemos dividiendo por el área

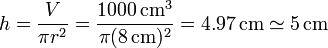
$h = \frac{V}{\pi r^2}=\frac{1000\,\mathrm{cm}^3}{\pi (8\,\mathrm{cm})^2}=4.97\,\mathrm{cm}\simeq 5\,\mathrm{cm}$

2.2 Superficie de contacto

Una vez que tenemos la altura a la que llega el área, calculamos la superficie de contacto como la suma de la base (un círculo) + más la cara lateral (un rectángulo), lo que nos da

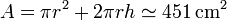
$A = \pi r^2 + 2\pi r h \simeq 451\,\mathrm{cm}^2$

2.3 Flujo de calor

El calor entra en el sistema desde el baño por conducción:

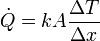
$\dot{Q}=k A\frac{\Delta T}{\Delta x}$

En la expresión del flujo de calor $Δ T$ la diferencia de temperaturas entre las dos caras

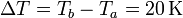
$\Delta T = T_b - T_a = 20\,\mathrm{K}$

y $Δ x$ el espesor del recipiente (0.01 m). Por tanto

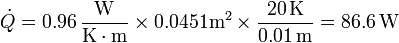
$\dot{Q}=0.96\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times 0.0451\mathrm{m}^2\times \frac{20\,\mathrm{K}}{0.01\,\mathrm{m}} = 86.6\,\mathrm{W}$

3 Fusión del hielo

3.1 Hielo fundido por segundo

La cantidad de hielo que se funde por segundo la hallamos dividiendo la cantidad de calor que entra en este tiempo por la cantidad de calor necesaria para fundir un kilogramo de hielo

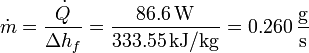
$\dot{m}=\frac{\dot{Q}}{\Delta h_f}=\frac{86.6\,\mathrm{W}}{333.55\,\mathrm{kJ}/\mathrm{kg}}=0.260\,\frac{\mathrm{g}}{\mathrm{s}}$

3.2 Tiempo total de fusión

A este ritmo se necesita un tiempo

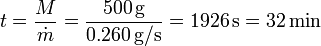
$t = \frac{M}{\dot{m}}= \frac{500\,\mathrm{g}}{0.260\,\mathrm{g}/\mathrm{s}} = 1926\,\mathrm{s}=32\,\mathrm{min}$

para fundir el hielo por completo. La cantidad de calor que entra en ese tiempo es

$\dot{Q}t = M\,\Delta h_f = 167\,\mathrm{kJ}$

Fusión de un trozo de hielo

De Laplace

Contenido

1 Enunciado

2 Flujo de calor

2.1 Altura del agua

2.2 Superficie de contacto

2.3 Flujo de calor

3 Fusión del hielo

3.1 Hielo fundido por segundo

3.2 Tiempo total de fusión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES