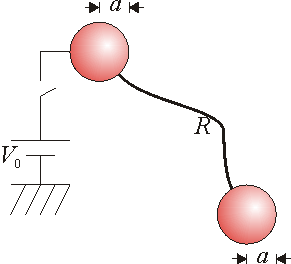
Problemas de corriente eléctrica
De Laplace
1 Flujo de líquido por una tubería
Por el interior de una tubería cilíndrica de radio a fluye un líquido con una velocidad, dependiente de la distancia al eje, ρ, como
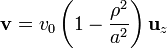
El líquido posee una densidad de carga uniforme ρ0, de forma que la densidad de corriente es 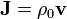 . En el exterior del tubo no hay corriente.
. En el exterior del tubo no hay corriente.
- Calcule la intensidad de corriente que atraviesa una sección por la tubería.
- Si se desea que por la superficie del tubo circule una corriente superficial
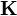 , de forma que la corriente total sea nula, ¿cuánto debe valer
, de forma que la corriente total sea nula, ¿cuánto debe valer 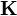 ?
?
2 Velocidad de arrastre
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
3 Nube de carga de radio variable
Una nube esférica de carga (compuesta de una distribución de cargas puntuales flotando en el vacío) se contrae y dilata, variando el radio de la esfera como R(t) = R0 + acos(ωt). La carga total de la nube, Q0, se encuentra distribuida en todo momento de forma uniforme en el volumen de la esfera.A partir de la ley de conservación de la carga, calcule la densidad de corriente de conducción en la nube. Puede suponer que 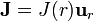 y que esta densidad no es infinita en el centro de la esfera.
y que esta densidad no es infinita en el centro de la esfera.
Calcule el campo eléctrico en los puntos del espacio y, a partir de éste, la corriente de desplazamiento. ¿Cuánto vale la densidad de corriente total?
¿Habrá campo magnético en el sistema?
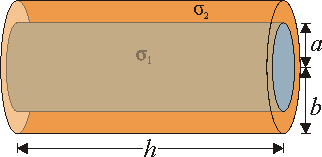
4 Resistencia de un tubo
Sea un tubo cilíndrico, de radio interior a y exterior b, y longitud h, de un material de conductividad σ. Calcule la resistencia eléctrica- Entre las dos bases.
- Entre la cara interior y la exterior.
5 Cable bimetálico
Entre los distintos tipos de cable empleados en la industria, se encuentra el de aluminio revestido de cobre. Está formado por un núcleo de aluminio de radio a (suponga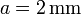 ), rodeado por una capa de cobre, de radio exterior b (sea
), rodeado por una capa de cobre, de radio exterior b (sea 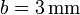 ).
).
- Calcule la resistencia de cable de esta clase de longitud
 .
.
- Determine la corriente que circula por cada metal cuando se aplica una diferencia de potencial
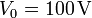 al cable anterior.
al cable anterior.
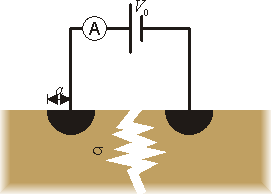
6 Conductividad del suelo
Para determinar la conductividad σ del suelo se mide la corriente entre dos electrodos clavados en tierra y sometidos a una cierta diferencia de potencial.- Suponga en primer lugar sólo un electrodo hemisférico de radio a, perfectamente conductor, puesto a un potencial V1 respecto a puntos muy alejados. En el estado estacionario, determínese la distribución de potencial en el suelo. Admita que el potencial depende exclusivamente de la distancia al centro del electrodo. A partir de este resultado, calcule la resistencia entre el electrodo y el infinito. Suponga que el suelo posee conductividad igual en todos sus puntos.
- Suponga ahora dos electrodos del tipo anterior, del mismo radio, y muy alejados entre sí. Si se conectan por el aire mediante un cable ideal y una fuente de continua de tensión V0, ¿qué corriente circula de un electrodo al otro?
- Si para una tensión de
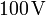 entre dos electrodos de
entre dos electrodos de 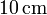 de radio se mide una corriente de
de radio se mide una corriente de 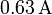 , ¿cuánto vale la conductividad del suelo?
, ¿cuánto vale la conductividad del suelo?
7 Corrientes atmosféricas
La resistividad del aire en la atmósfera decrece exponencialmente con la altura como
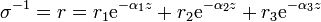
donde

El campo eléctrico en zonas despejadas de la superficie de la Tierra vale 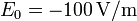 . Este campo es prácticamente constante y va siempre en la dirección vertical.
. Este campo es prácticamente constante y va siempre en la dirección vertical.
A partir de estos datos halle
- El valor del campo eléctrico para un punto situado entre la superficie de la Tierra y la ionosfera (
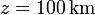 ).
).
- La diferencia de potencial entre la superficie y la ionosfera.
- La distribución de cargas en la atmósfera.
- La corriente total que llega a la superficie de la Tierra.
- La potencia necesaria para mantener esta corriente estacionaria
- Estime el tiempo que tardaría la atmósfera en descargarse si no existiera un mecanismo generador
8 Resistencia de una soldadura
Tras una rotura de un cable de cobre (de resistividad r1) de sección S y gran longitud, se procede a unir los dos pedazos mediante una soldadura. Como consecuencia de la presencia de óxido la resistividaddel cable aumenta hasta un valor r2 en una región alrededor del punto de contacto, pudiéndose describir matemáticamente según la ley
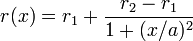
- Calcule el aumento de la resistencia total del cable. Aplíquese al caso
 ,
, 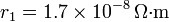 ,
, 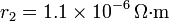 ,
, 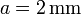 .
.
- Si la potencia máxima por unidad de volumen que soporta el hilo antes de fundirse es
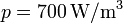 , determine la intensidad de corriente máxima que puede circular por el cable antes de la soldadura y después de ella.
, determine la intensidad de corriente máxima que puede circular por el cable antes de la soldadura y después de ella.
9 Matriz de conductancia de bloques
Se tiene un sistema de cuatro electrodos tal como se indica en la figura. Uno de ellos (electrodo "0") es un prisma cuadrado hueco de lado interior 43 mm y longitud 50 mm. Este electrodo se encuentra siempre a tierra.
En su interior se encuentran tres conductores perfectos. El electrodo "1" es un paralelepípedo de lados 41 mm, 20 mm y 50 mm. Los electrodos "2" y "3" son sendos prismas cuadrados de lado 20 mm y altura 50 mm. la distancia entre superficies conductoras vecinas es de 1 mm.
Todo el espacio entre los distintos electrodos (pero no el exterior al conductor 0) se encuentra lleno de un material óhmico de conductividad 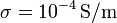
- Teniendo en cuenta la pequeñez relativa de las diferentes distancias calcule, aproximadamente, la matriz de coeficientes de conductancia en este sistema.
- Halle las corrientes que llegan a los conductores 1, 2 y 3, cuando se encuentran conectados a generadores que fijan sus tensiones en
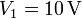 ,
, 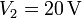 y
y 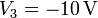 .
.
- Para la configuración anterior, calcule la potencia disipada en el sistema.
- Si el electrodo 2 se encuentra a tensión
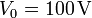 , el 1 se deja desconectado y el 3 se pone a tierra, ¿cuáles son las corrientes que llegan a cada conductor y las tensiones de cada uno? ¿Y si también se desconecta el 3?
, el 1 se deja desconectado y el 3 se pone a tierra, ¿cuáles son las corrientes que llegan a cada conductor y las tensiones de cada uno? ¿Y si también se desconecta el 3?
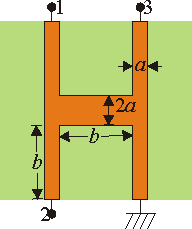
10 Pista en forma de H
Se tiene un circuito impreso en forma de "H" de un material de conductividad σ, con cuatro terminales, una de las cuales se encuentra permanentemente a tierra. Los brazos de la H y el tabique central poseen longitud b. Los cuatro brazos tienen anchura a, (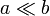 ) mientras que el tramo central posee anchura 2a, según indica la figura. El espesor de toda la pista es c.
) mientras que el tramo central posee anchura 2a, según indica la figura. El espesor de toda la pista es c.
- Determine la matriz de los coeficientes de conductancia, Gij, correspondiente a los tres terminales libres. Desprecie la pequeña contribución de las esquinas donde confluyen los brazos.
- A partir de la matriz anterior, calcule las conductancias
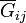 y elabore un circuito equivalente al sistema de tres electrodos, que no emplee nodos intermedios.
y elabore un circuito equivalente al sistema de tres electrodos, que no emplee nodos intermedios.
- Determine la potencia consumida en la pista cuando el terminal 1 se encuentra a potencial V0 y los otros a tierra.
- En la configuración anterior se corta la conexión a tierra del electrodo 2. En el nuevo estado estacionario, ¿se consume más o menos potencia que antes de la desconexión? ¿Cuánto?
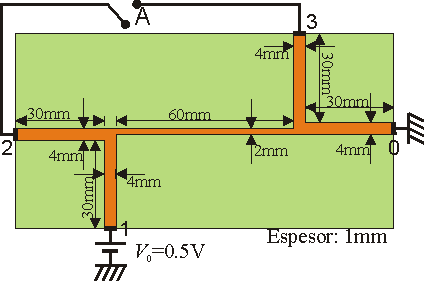
11 Pista con varias terminales
Se tiene un modelo de circuito integrado formado por una pista con las dimensiones indicadas en la figura. La pista es de grafito (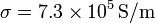 ). El espesor de la pista vale
). El espesor de la pista vale  en todas partes. La anchura de cada segmento rectilíneo es
en todas partes. La anchura de cada segmento rectilíneo es 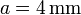 , salvo el central, que tiene una anchura de
, salvo el central, que tiene una anchura de 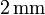 . Todas las fuentes y conexiones exteriores son ideales (sin resistencia).
. Todas las fuentes y conexiones exteriores son ideales (sin resistencia).
- Inicialmente el interruptor A está abierto. Calcule el valor aproximado de la corriente que entra por el electrodo 1, cuando el electrodo 1 está a una tensión de 0.5 V y el electrodo 0 está a tierra.
- ¿Cuánto vale aproximadamente la potencia disipada en el sistema en la situación anterior?
- Suponga que se cierra el interruptor A. ¿Cómo cambia la corriente que entra por el electrodo 1? ¿Y la potencia consumida?
- En la situación del apartado anterior, ¿cuánto vale aproximadamente la densidad de corriente en cada tramo recto del circuito? ¿Y la potencia disipada por unidad de volumen?
12 Modelo esférico de generador
Como modelo ideal de generador suponga el siguiente sistema: una esfera de radio a de conductividad σ1 se encuentra inmersa en un medio de conductividad σ2 que se extiende hasta el infinito. En el interior de la esfera actúa una fuerza no electrostática por unidad de carga 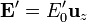 , constante y uniforme.
, constante y uniforme.
- Escriba las ecuaciones y condiciones de salto para la densidad de corriente, el campo y el potencial eléctrico en todo el espacio.
- Sabiendo que en el interior de la esfera el potencial es de la forma
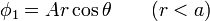
- y en el exterior de ella
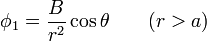
- calcule las constantes A y B.
- Halle la potencia desarrollada por el campo eléctrico en el interior y el exterior de la esfera.
- Considerando que la corriente es la que atraviesa el plano ecuatorial de la esfera (z = 0, r < a) determine la fuerza electromotriz, la resistencia interna y la externa del circuito equivalente.
- ¿A qué tienden los resultados cuando
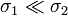 ? ¿Y cuando
? ¿Y cuando 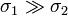 ?
?
13 Descarga de un condensador
Entre dos placas planas y paralelas, perfectamente conductoras, de sección S, y separadas una distancia a se encuentra un medio resistivo, de permitividad  y conductividad σ. Entre las placas hay establecida una tensión V0.
y conductividad σ. Entre las placas hay establecida una tensión V0.
- Halle la corriente que circula entre las placas y la carga almacenada en cada una, así como la energía almacenada en el sistema.
- En t = 0 se desconecta el generador. Determine la evolución de la carga en las placas a partir de ese momento.
- Halle la energía disipada en el medio durante el proceso de descarga del condensador.
- Describa el comportamiento del sistema mediante un circuito equivalente.
14 Carga de un condensador parcialmente relleno
Entre dos placas planas y paralelas separadas una distancia a + b se coloca una capa de espesor a de un medio de permitividad y conductividad σ. El resto del espacio lo ocupa una capa de espesor b vacía.
y conductividad σ. El resto del espacio lo ocupa una capa de espesor b vacía.
En el instante t = 0 se conecta una diferencia de potencial V0.
- ¿Cuánto valen
 ,
,  y
y 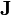 inmediatamente después de conectar el potencial?
inmediatamente después de conectar el potencial?
- ¿Cuánto valen un tiempo largo después de que se haya establecido?
- ¿Cuánto valen en cualquier instante?
- ¿Cómo varía, durante el periodo transitorio, la energía almacenada en el sistema? ¿Cuánta energía se disipa durante este periodo? ¿De dónde procede esta energía?
- Si en lugar de una tensión escalón se aplica durante un largo periodo de tiempo un voltaje alterno V = V0cos(ωt)
- ¿Cuánto vale la corriente que llega al elemento? ¿Cuál es la impedancia del sistema? ¿Y el circuito equivalente?
- ¿Cuanto vale la energía aportada por el generador en un periodo? ¿En qué se emplea esta energía?
15 Descarga de un sistema "corte de helado"
Un medio óhmico de permitivida , conductividad σ y sección S / 2 rellena parcialmente el espacio entre dos placas planas y paralelas perfectamente conductoras, ambas de sección S y separadas una distancia a. La otra mitad del espacio entre las placas queda vacío.
, conductividad σ y sección S / 2 rellena parcialmente el espacio entre dos placas planas y paralelas perfectamente conductoras, ambas de sección S y separadas una distancia a. La otra mitad del espacio entre las placas queda vacío.
Inicialmente el sistema se halla en estado estacionario, con una diferencia de potencial $V_0$ entre las placas
- Determine los campos
 ,
, 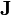 y
y  en el sistema, así como las densidades (volumétricas y superficiales) de carga libre y de polarización.
en el sistema, así como las densidades (volumétricas y superficiales) de carga libre y de polarización.
- Calcule la energía eléctrica almacenada y la potencia que se disipa en el sistema en este estado estacionario.
- En t = 0 se desconecta el generador, quedando el circuito abierto
- Determine los campos
 ,
, 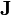 y
y  y las distribuciones de carga en el sistema cuando, pasado un tiempo largo, se alcanza de nuevo un estado estacionario.
y las distribuciones de carga en el sistema cuando, pasado un tiempo largo, se alcanza de nuevo un estado estacionario.
- Determine la evolución temporal de estos campos y cargas para todo t > 0.
- ¿Cuánta energía se disipa en el proceso?
- Determine los campos
- Si en lugar de una tensión escalón se aplica durante un largo periodo de tiempo un voltaje alterno V = V0cos(ωt)
- ¿Cuánto vale la corriente que llega al elemento? ¿Cuál es la impedancia del sistema? ¿Y el circuito equivalente?
- ¿Cuanto vale la energía aportada por el generador en un periodo? ¿En qué se emplea esta energía?
16 Condensador sometido a un voltaje en rampa
Entre dos placas metálicas, planas y paralelas, de sección S, y separadas una distancia a, se encuentra un medio óhmico de permitividad  y conductividad σ.
y conductividad σ.
Ambas placas están conectadas a sendos generadores de tensión variable.
- Inicialmente ambas placas se encuentran a tierra. Entonces, la tensión de la placa 1 se varía gradualmente de 0 a V0 en un tiempo T como V1(t) = V0t / T. Determine la corriente que llega a esta placa durante este tiempo.
- Para el periodo anterior, calcule la energía disipada en el medio óhmico, así como la energía aportada por el generador en este intervalo. ¿Coinciden estas dos cantidades? Si no lo hacen, ¿a qué se debe su diferencia?
- Una vez que la placa 1 se encuentra a tensión V0, el potencial de la placa 2 comienza a elevarse hasta el mismo valor, requiriendo de nuevo un periodo T para alcanzar el valor límite. ¿Cuánta corriente llega a la placa 1 durante este intervalo? ¿Y a la placa 2?
- Durante este segundo periodo, ¿cuánta energía se disipa en el medio? ¿Cuánta aporta cada generador? ¿Se verifica el balance energético?
17 Dos esferas alejadas
Dos esferas metálicas, perfectamente conductoras, de radio a, se encuentran muy alejadas la una de la otra (de forma que no se influyen entre sí). Las dos esferas se encuentran conectadas mediante un cable de resistencia R. Una de las esferas se encuentra conectada a un generador de tensión V0, a través de un interruptor que inicialmente se encuentra abierto. Ambas esferas están inicialmente descargadas.- Suponga que el interruptor se cierra durante un periodo de tiempo muy corto (el imprescindible para que se cargue la esfera conectada a él) y se vuelve a abrir. Justo tras este intervalo ¿cómo es la distribución de cargas y potenciales en las esferas? ¿Cuánto vale la energía electrostática almacenada en el sistema?
- Si se deja transcurrir un periodo de tiempo largo, ¿cómo queda la distribución de cargas y potenciales? ¿Cuál es la energía electrostática almacenada en el sistema en el estado final?
- Determine la evolución en el tiempo de las cargas y potenciales en cada esfera, así como la corriente que circula por el cable.
- Halle la energía disipada en el cable durante el periodo transitorio y verifique que se satisface el balance energético.
- Suponga ahora que, en el proceso anterior, el generador no se desconecta, sino que se deja permanentemente conectado a la primera esfera. En ese caso, ¿cómo varía la carga en cada esfera? ¿Y la corriente por el cable? ¿Y la energía disipada y la energía almacenada?
- Si en lugar de una tensión escalón se aplica a la esfera durante un largo periodo de tiempo un voltaje alterno V = V0cos(ωt)
- ¿Cuánto vale la corriente que llega a esta esfera? ¿Cuál es la impedancia del sistema? ¿Y el circuito equivalente?
- ¿Cuanto vale la energía aportada por el generador en un periodo? ¿En qué se emplea esta energía?
18 Despolarización de una esfera
Una esfera de radio a se despolariza según la ley
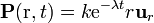
Determine las densidades de carga de polarización, así como la densidad de corriente de polarización. ¿Se verifica la ley de conservación de la carga para ρp y σp?
19 Campos en un condensador sometido a un voltaje alterno
Suponga que se sumergen dos conductores perfectos en un material de permitividad  y conductividad σ. Si se aplica entre ellos una diferencia de potencial constante V0 la corriente que llega a uno de ellos vale I0. ¿Cuál será la corriente si el voltaje varía como V0cosωt?
y conductividad σ. Si se aplica entre ellos una diferencia de potencial constante V0 la corriente que llega a uno de ellos vale I0. ¿Cuál será la corriente si el voltaje varía como V0cosωt?