Problemas de Cinemática del punto (G.I.A.)
De Laplace
Contenido |
1 Problemas del boletín
1.1 Ecuaciones de curvas
Expresa en forma parámetrica e implícita las siguientes curvas
- El eje OY
- Una circunferencia de radio a, contenida en el plano XY y con centro en el origen.
- Una parábola contenida en el plano YZ y con ecuación z = y2.
1.2 Trayectoria de una partícula
La trayectoria de una partícula viene dada por la ley horaria
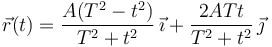
Determina la velocidad y aceleración de la partícula, los vectores del triedro intrínseco, así como la ecuación de la trayectoria. Calcula también las componentes intrínsecas de la velocidad y la aceleración ¿Cual es la expresión de un desplazamiento elemental 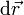 ? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula.
? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula.
1.3 Tiro oblicuo
Determina el movimiento de un proyectil disparado con una velocidad inicial v0 y un ángulo α con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria.
1.4 Cuerda enrollándose
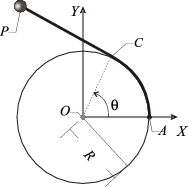
Una partícula se mueve en el plano OXY mientras permanece
conectada a uno de los extremos de un hilo inextensible de longitud
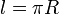 . El otro extremo está unido a un punto fijo A de una
circunferencia de radio R y centro O, cuyas coordenadas en el
sistema cartesiano OXY son
. El otro extremo está unido a un punto fijo A de una
circunferencia de radio R y centro O, cuyas coordenadas en el
sistema cartesiano OXY son 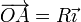 . Partiendo
de la posición inicial
. Partiendo
de la posición inicial 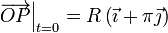 , el movimiento de la partícula con velocidad de módulo
constante v0 da lugar a que el hilo, que permanece siempre tenso,
se enrolle en dicha circunferencia. Utilizando como parámetro el
ángulo θ correspondiente al punto C donde desaparece el
contacto hilo--circunferencia, calcula:
, el movimiento de la partícula con velocidad de módulo
constante v0 da lugar a que el hilo, que permanece siempre tenso,
se enrolle en dicha circunferencia. Utilizando como parámetro el
ángulo θ correspondiente al punto C donde desaparece el
contacto hilo--circunferencia, calcula:
- Las ecuaciones paramétricas de la trayectoria seguida por la partícula.
- La ley horaria del movimiento θ = θ(t) y tiempo que tarda el hilo en enrollarse completamente sobre la circunferencia.
- La aceleración de la partícula.
- El triedro intrínseco de la trayectoria seguida por la partícula
1.5 Velocidad de un punto en la superficie de la Tierra
La Tierra rota uniformemente con respecto a su eje con velocidad angular ω constante. Encuentra en función de
la latitud λ, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: 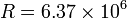 m.)
m.)
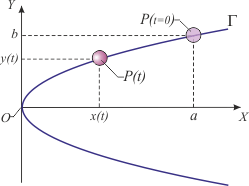
1.6 Punto moviéndose sobre una parábola
Un punto inicialmente en reposo en la posición x = a, y = b,describe la parábola 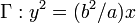 . Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
. Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
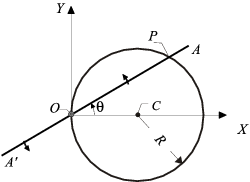
1.7 Barra deslizando sobre una circunferencia
En un plano OXY, se define el sistema cinemático formado por los dos siguientes elementos geométricos:
- una circunferencia fija, de radio R y centrada en el punto C de coordenadas
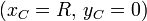 ;
;
- un segmento rectilíneo móvil A'A, de longitud superior a 4R, el cual gira con velocidad angular constante ω (en sentido antihorario) alrededor de un eje fijo que pasa por su punto medio O y es normal al plano OXY (eje OZ).
Sabiendo que el ángulo θ ( que forman OA y OX) es nulo en el instante inicial (t = 0); y considerando como móvil problema el punto P en el que se cortan el segmento A'A y la circunferencia , se pide:
- item Determinar las ecuaciones horarias,
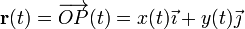 , del punto P, así como sus vectores velocidad,
, del punto P, así como sus vectores velocidad, 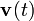 , y aceleración,
, y aceleración, 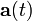 .
.
- Calcular las aceleraciones tangencial y normal de dicho punto P.
1.8 Parámetro arco de una hélice
Sea la hélice Γ descrita en un sistema de referencia cartesiano OXYZ por las siguientes ecuaciones paramétricas:
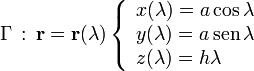
donde a y h son constantes conocidas.
- Determina la longitud recorrida sobre la hélice (parámetro arco) en función del parámetro λ
- Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
- Calcula su radio de curvatura.