Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del sólido rígido (GIE)

De Laplace

(Diferencias entre revisiones)
m (→Diferentes movimientos de una esfera)
(→Ejemplo gráfico de movimiento plano)
Línea 152: Línea 152:
# En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?
# En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?
# ¿Dónde se encuentra el centro instantáneo de rotación?
# ¿Dónde se encuentra el centro instantáneo de rotación?
 +
 +
==[[Comparación de posibles movimientos planos]]==
 +
De las siguientes cuatro figuras, solo una representa velocidades
 +
posibles de los extremos A y B de una barra rígida que realiza un movimiento
 +
plano.
 +
 +
# ¿Cuál es la figura correcta?
 +
# Para la barra anterior, ¿dónde se encuentra su centro instantáneo de rotación, según la cuadrícula de la figura?
 +
# ¿Cuánto vale, en rad/s, la velocidad angular instantánea de este movimiento, si la cuadrícula representa m en distancias y m/s en velocidades?
==[[Deslizamiento entre dos rodillos]]==
==[[Deslizamiento entre dos rodillos]]==

Revisión de 22:01 4 feb 2013

Contenido

1 Caso de campo de velocidades de un sólido

El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional

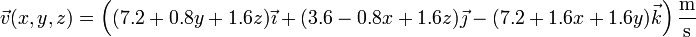
\vec{v}(x,y,z)=\left((7.2 + 0.8 y + 1.6 z)\vec{\imath}+(3.6 - 0.8 x + 1.6 z)\vec{\jmath} -(7.2+1.6 x+1.6 y)\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}
  1. Determine la velocidad angular, \vec{\omega}, y la velocidad del origen de coordenadas, \vec{v}_0.
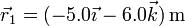  2. Halle la velocidad del punto \vec{r}_1=(-5.0\vec{\imath}-6.0\vec{k})\,\mathrm{m}.
  3. ¿Qué tipo de movimiento describe el sólido en este instante?
  4. Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o eje instantáneo de rotación, en su caso).

2 Movimiento de un sólido conocido un eje

Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector 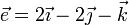\vec{e}=2\vec{\imath}-2\vec{\jmath}-\vec{k}, de tal forma que la velocidad del punto B(0,2,1) es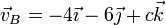 \vec{v}_B=-4\vec{\imath}-6\vec{\jmath}+c\vec{k}

  1. Halle el valor de la constante c.
  2. Calcule la velocidad angular instantánea.
  3. Calcule la velocidad del punto P(1,1,0).

Todas las cantidades están expresadas en las unidades del SI.

3 Clasificación de movimientos de un sólido

Se tiene un sólido formado por ocho masas iguales, 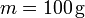m=100\,\mathrm{g}, situadas en los vértices de un cubo de lado 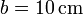b=10\,\mathrm{cm}. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.

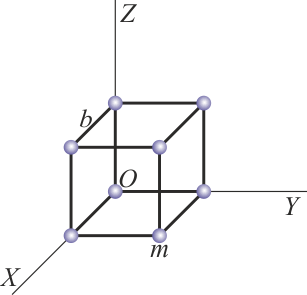
Archivo:ocho-masas.png

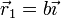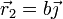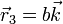
Considere los casos siguientes para las velocidades de las masas situadas en \vec{r}_1=b\vec{\imath}, \vec{r}_2=b\vec{\jmath} y \vec{r}_3=b\vec{k}

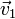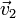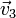Caso \vec{v}_1 (cm/s) \vec{v}_2 (cm/s) \vec{v}_3 (cm/s)
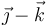
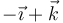
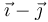
I \vec{\jmath}-\vec{k} -\vec{\imath}+\vec{k} \vec{\imath}-\vec{\jmath}
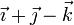
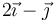
II \vec{\imath}+\vec{\jmath}-\vec{k} \vec{k} 2\vec{\imath}-\vec{\jmath}
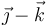
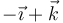
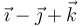
III \vec{\jmath}-\vec{k} -\vec{\imath}+\vec{k} \vec{\imath}-\vec{\jmath}+\vec{k}
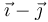
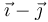
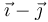
IV \vec{\imath}-\vec{\jmath} \vec{\imath}-\vec{\jmath} \vec{\imath}-\vec{\jmath}
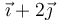
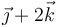
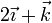
V \vec{\imath}+2\vec{\jmath} \vec{\jmath}+2\vec{k} 2\vec{\imath}+\vec{k}
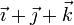
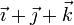
VI \vec{\imath}+\vec{\jmath}+\vec{k} \vec{\imath}+\vec{\jmath}+\vec{k} \vec{0}
  1. Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
  2. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
  3. Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
  4. Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.

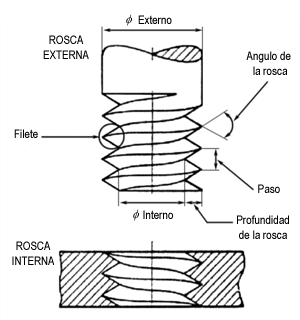
4 Rapidez de los puntos de un tornillo

Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo.

Archivo:tornillo.png

5 Rodadura y deslizamiento de un disco

Un disco de radio R y masa M rueda y desliza sobre el plano horizontal y = 0 de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma

\vec{v}_A = v_A\vec{\imath}\qquad \vec{v}_B = v_B\vec{\imath}
  1. Calcule la velocidad angular del disco.
  2. Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
  3. Determine la posición del centro instantáneo de rotación.
  4. Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
    1. vA = − vB
    2. vA = 0
    3. vA = vB

6 Rodadura y pivotamiento de una pelota

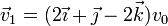Una pelota de radio R rueda y pivota sin deslizar sobre el plano horizontal z = 0, de forma que las velocidades de los puntos \vec{r}_1=(\vec{\imath}+\vec{k})R y \vec{r}_2=(-\vec{\imath}+\vec{k})R valen respectivamente \vec{v}_1=(2\vec{\imath}+\vec{\jmath}-2\vec{k})v_0 y \vec{v}_2=(2\vec{\imath}+3\vec{\jmath}+2\vec{k})v_0.

  1. Determine la velocidad angular de rodadura y la de pivotamiento.
  2. Halle la velocidad del centro de la bola.
  3. Determine la ecuación del eje instantáneo de rotación.

7 Diferentes movimientos de una esfera

Considérese una esfera de masa M y radio R que se mueve sobre la superficie horizontal z = 0. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula

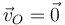
\vec{v}_O = \vec{0}

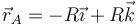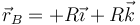Para este mismo instante la velocidad de los puntos \vec{r}_A=-R\vec{\imath}+R\vec{k} y \vec{r}_B=+R\vec{\imath}+R\vec{k} situados en un diámetro horizontal valen respectivamente

\vec{v}_A = v_A\vec{\jmath}\qquad \vec{v}_B = v_B\vec{\jmath}

Para los tres casos siguientes:

  • vA = + vB
  • vA = 0
  • vA = − vB
  1. Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
  2. Calcule la velocidad angular del sólido.
  3. Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
  4. Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
  5. Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.

8 Deslizamiento de una barra

Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una distancia de 60 cm de la esquina y se mueve con velocidad de 12 cm/s alejándose de la esquina

  1. ¿Con qué velocidad se mueve el extremo superior de la barra?
  2. Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OZ, ¿dónde se encuentra el C.I.R. de la barra en el instante anteriormente descrito?

9 Movimiento de un sistema biela-manivela

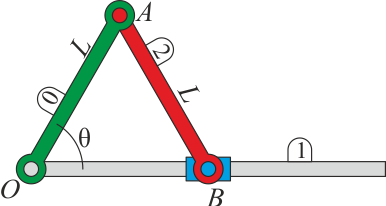
Un sistema biela-manivela está formado por: una barra fija (el eje “1”); una barra (la manivela “0”) de longitud L, articulada en el punto O del eje y que forma un ángulo θ(t) con él; y una segunda barra (la biela “2”), también de longitud L, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje.

  1. Halle las velocidades de los puntos A y B de la biela.
  2. Determine la velocidad angular de la biela respecto al eje.
  3. Localice el centro instantáneo de rotación (CIR) de la biela respecto al eje.
  4. Suponga el caso 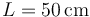L=50\,\mathrm{cm} y que en un instante dado tg(θ) = 0.75 siendo 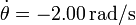\dot{\theta}=-2.00\,\mathrm{rad}/\mathrm{s}. Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.
Archivo:esquema-biela-manivela.png

10 Barra articulada rotatoria

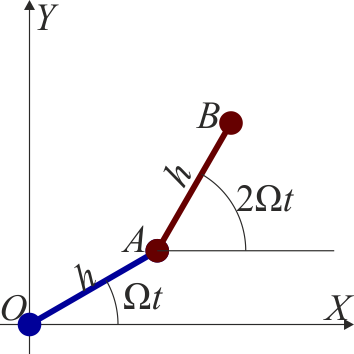
Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud h situadas sobre una superficie horizontal. La primera barra tiene un extremo O fijo, de forma que gira alrededor de él con velocidad angular constante Ω respecto a un sistema de ejes fijos OXY. La segunda barra está articulada en el extremo A de la primera y gira respecto de los mismos ejes fijos con una velocidad angular 2Ω. En el instante t = 0 el sistema está completamente extendido a lo largo del eje OX.

  1. Calcule la velocidad del punto de articulación A y del extremo libre B de la segunda barra en el instante t = 0.
  2. Localice la posición del centro instantáneo de rotación I del movimiento de la segunda barra respecto a los ejes fijos para el instante t = 0.
  3. Determine la posición del extremo B cuando ha pasado medio periodo, t = π / Ω, así como la velocidad de este punto en ese instante.
  4. Escriba las ecuaciones horarias de la posición del punto B para todo instante.
  5. Calcule la aceleración del extremo B de la barra en el instante t = 0. ¿Es nula alguna de sus componentes intrínsecas?
Archivo:barras-articuladas-rotatorias.png

11 Ejemplo gráfico de movimiento plano

En un movimiento plano, se tiene que la velocidad instantánea de dos puntos A y B es la ilustrada en la figura (para la posición, la cuadrícula representa cm y para la velocidad cm/s)

  1. En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?
  2. ¿Dónde se encuentra el centro instantáneo de rotación?

12 Comparación de posibles movimientos planos

De las siguientes cuatro figuras, solo una representa velocidades posibles de los extremos A y B de una barra rígida que realiza un movimiento plano.

  1. ¿Cuál es la figura correcta?
  2. Para la barra anterior, ¿dónde se encuentra su centro instantáneo de rotación, según la cuadrícula de la figura?
  3. ¿Cuánto vale, en rad/s, la velocidad angular instantánea de este movimiento, si la cuadrícula representa m en distancias y m/s en velocidades?

13 Deslizamiento entre dos rodillos

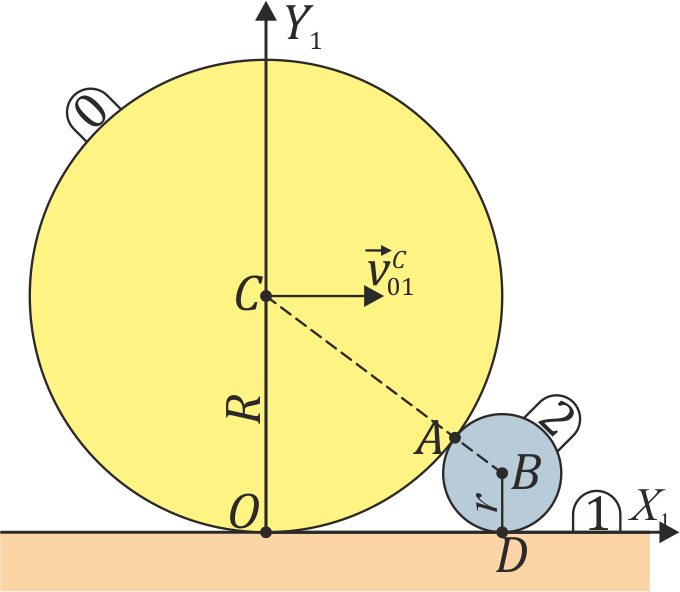
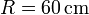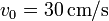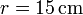Un rodillo de radio R=60\,\mathrm{cm} (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante v_0=30\,\mathrm{cm}/\mathrm{s} respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio r=15\,\mathrm{cm} (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).

Halle la velocidad relativa de deslizamiento en el punto A de contacto entre los dos sólidos. ¿Cuál es la rapidez de este deslizamiento?

Archivo:Dos-rodillos-01.png

14 Clasificación de movimientos de un sólido (versión 2011)

Se tiene un sólido formado por ocho masas iguales, 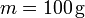m=100\,\mathrm{g}, situadas en los vértices de un cubo de lado 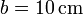b=10\,\mathrm{cm}. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.

Archivo:ocho-masas.png

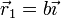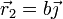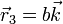
Considere los casos siguientes para las velocidades de las masas situadas en \vec{r}_1=b\vec{\imath}, \vec{r}_2=b\vec{\jmath} y \vec{r}_3=b\vec{k}

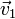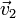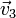Caso \vec{v}_1 (cm/s) \vec{v}_2 (cm/s) \vec{v}_3 (cm/s)
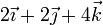
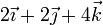
I 2\vec{\imath}+2\vec{\jmath}+4\vec{k} 2\vec{\imath}+2\vec{\jmath}+4\vec{k} 2\vec{k}
II 2\vec{\imath}+\vec{\jmath}+2\vec{k} 3\vec{\imath}+2\vec{\jmath} 2\vec{\imath}+4\vec{\jmath} + 2\vec{k}
III 2\vec{\imath}+2\vec{\jmath}+2\vec{k} 2\vec{\imath}+2\vec{\jmath}+2\vec{k} 2\vec{\imath}+2\vec{\jmath}+2\vec{k}
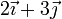
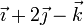
IV 2\vec{\imath}+3\vec{\jmath} \vec{\imath}+2\vec{\jmath}-\vec{k} 4\vec{\imath}+4\vec{\jmath}+2\vec{k}
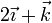
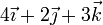
V 2\vec{\imath}+\vec{k} 4\vec{\imath}+2\vec{\jmath}+3\vec{k} 3\vec{\imath}+\vec{\jmath}+2\vec{k}
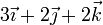
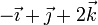
VI 2\vec{\imath}+\vec{\jmath}+2\vec{k} 3\vec{\imath}+2\vec{\jmath}+2\vec{k} -\vec{\imath}+\vec{\jmath}+2\vec{k}
  1. Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
  2. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
  3. Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
  4. Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.

15 Rodadura permanente de un disco

La rodadura permanente de un disco de radio R sobre una superficie horizontal puede describirse mediante el campo de velocidades

\vec{v}(\vec{r}) = \vec{v}_0 +\vec{\omega}\times\vec{r}\qquad \qquad \vec{v}_0 = v_0\vec{\imath}\qquad\vec{\omega}=-\frac{v_0}{R}\vec{k}

donde la superficie horizontal se encuentra en y = − R.

Determine, para un instante dado, la velocidades de los puntos A, B, C y D situados en los cuatro cuadrantes del disco. ¿Cuál es el eje instantáneo de rotación?

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_s%C3%B3lido_r%C3%ADgido_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace