Clasificación de movimientos de un sólido
De Laplace
Contenido |
1 Enunciado
Se tiene un sólido formado por ocho masas iguales, 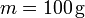 , situadas en los vértices de un cubo de lado
, situadas en los vértices de un cubo de lado 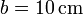 . En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
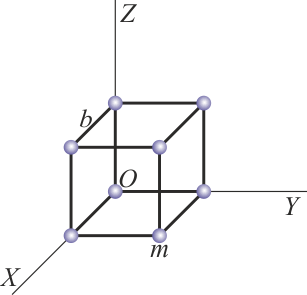
Considere los casos siguientes para las velocidades de las masas situadas en 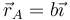 ,
, 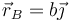 y
y 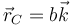
| Caso | 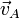 (cm/s) (cm/s)
| 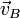 (cm/s) (cm/s)
| 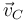 (cm/s) (cm/s)
|
|---|---|---|---|
| I | 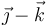
| 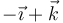
| 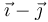
|
| II | 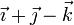
| 
| 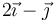
|
| III | 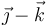
| 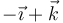
| 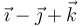
|
| IV | 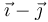
| 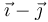
| 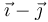
|
| V | 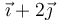
| 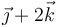
| 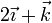
|
| VI | 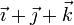
| 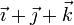
| 
|
- Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
- Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
- Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
2 Introducción
Para cada uno de los casos, el procedimiento es el siguiente:
- Se comprueba si verifican la condición cinemática de rigidez, de forma que para cada par de puntos
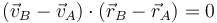
- Si no se cumple, ya hemos acabado.
- Si mira si las velocidades de los tres puntos son iguales. Si lo son, el movimiento es una traslación con dicha velocidad. En particular, si hay tres puntos no alineados con velocidad nula, el estado es de reposo.
- Si no ocurre lo anterior, pero uno de los puntos tiene velocidad nula, el movimiento es una rotación alrededor de un eje que pasa por este punto. La velocidad angular se saca de la velocidad de los otros puntos.
- Si dos puntos tienen la misma velocidad y el tercero no, el EIRMD (o EIR en su caso) apunta en la dirección de la recta que pasa por los dos puntos. De aquí se saca la velocidad de deslizamiento y de la velocidad del tercer punto la velocidad angular.
- Si no se aplica nada de lo anterior, hay que recurrir a la expresión del teorema de Chasles
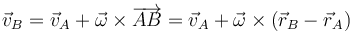
- para hallar el vector ω.
- Una vez que se tiene la velocidad angular, se calcula la velocidad de deslizamiento (igual para todos los puntos), tomando un punto cualquiera y hallando
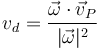
- Si esta velocidad es nula, el movimiento es una rotación. Si es distinta de cero, se trata de un movimiento helicoidal.
- El EIR o EIRMD, si no se ha localizado previamente, se determina empleando la fórmula
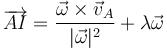
- que nos da la posición de los puntos del eje respecto al punto A.
3 Caso I
Tenemos que, midiendo las distancias en cm y las velocidades en cm/s
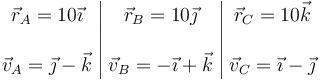
Comprobamos en primer lugar la condición de rigidez. Para el par AB
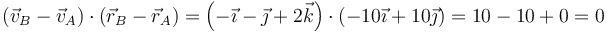
Para el AC

Para el BC
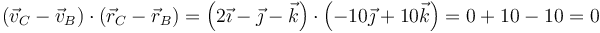
En los tres casos se satisface la condición. Por tanto, este es un posible movimiento de un sólido rígido.
Las tres velocidades no son iguales. Por tanto, no se trata de un movimiento de traslación.
No hay dos iguales, ni ninguna es nula, por lo que aun no podemos decir nada sobre el tipo de movimiento.
Recurrimos entonces al teorema de Chasles. Suponemos una velocidad angular genérica
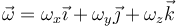
y la aplicamos a la relación entre las velocidades de A y B
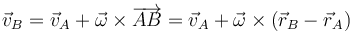
nos queda
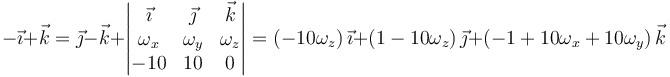
Igualando componente a componente llegamos al sistema de ecuaciones
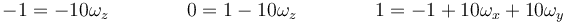
que nos dice que

Aun no tenemos las tres componentes, porque para determinar completamente el movimiento de un sólido necesitamos las velocidades de tres puntos no alineados. Aplicando de nuevo el teorema de Chasles al par AC
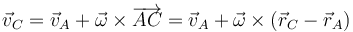
nos queda
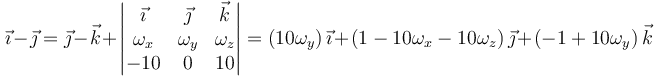
Igualando y despejando llegamos a

que con las ecuaciones anteriores nos dan la velocidad angular completa

Podría parecer excesivo que necesitamos seis ecuaciones para determinar tres incógnitas, pero la condición de rigidez nos garantiza que no son incompatibles y que son justo las necesarias.
Una vez que tenemos la velocidad angular, hallamos la velocidad de deslizamiento, a partir de la velocidad de cualquiera de los puntos
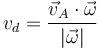
que nos da
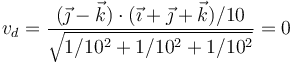
Al ser nula, el movimiento del sólido es de rotación.
Hallamos la ecuación del eje instantáneo de rotación mediante la fórmula
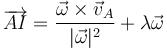
donde
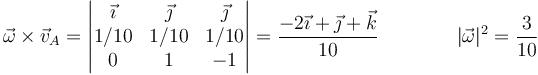
lo que nos da
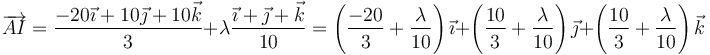
Esta es la posición respecto al punto A. Dado el sistema de referencia que estamos empleando, es preferible escribir la posición del eje respecto al origen de coordenadas O. Esto lo conseguimos con la suma vectorial
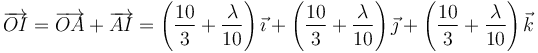
Ahora bien, en la expresión anterior, λ es un parámetro arbitrario. Simplemente nos sirve para etiquetar loa diferentes puntos del eje. Sin pérdida de generalidad podemos definir el nuevo parámetro
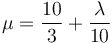
de forma que el eje se escribe en la forma mucho más simple
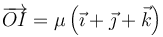
Esta expresión nos dice que el eje pasa por el origen de coordenadas, uy que su dirección la da el vector (1,1,1), que apunta en la diagonal del cubo.
4 Caso II
Operamos igualmente en el segundo caso. En primer lugar chequeamos la condición de rigidez.
Para el par AB
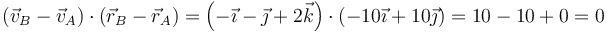
Para el AC

Para el BC
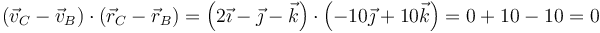
Todos los cálculos son idénticos al del apartado anterior, ya que las diferencias entre velocidades son las mismas. Si nos fijamos, vemos que las tres velocidades se obtienen de las del caso I sumando  a cada una, por lo que si allí eran compatibles con la rigidez, aquí también lo son.
a cada una, por lo que si allí eran compatibles con la rigidez, aquí también lo son.
Como en el apartado anterior, aplicamos el teorema de Chasles para determinar la velocidad angular. Los cálculos son de nuevo idénticos a los del apartado anterior, ya que en ellos solo se necesitan las diferencias de velocidades entre dos puntos. El resultado es
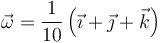
Podría parecer excesivo que necesitamos seis ecuaciones para determinar tres incógnitas, pero la condición de rigidez nos garantiza que no son incompatibles y que son justo las necesarias.
Una vez que tenemos la velocidad angular, hallamos la velocidad de deslizamiento, a partir de la velocidad de cualquiera de los puntos
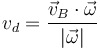
que nos da
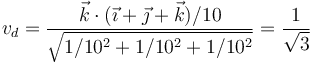
Puesto que en este caso no es nula, el movimiento del sólido es helicoidal.
Hallamos ahora la posición del EIRMD respecto a uno de los puntos. Puesto que B es el que tiene la velocidad más simple, lo hacemos respecto a éste
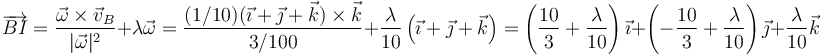
Si queremos la posición del eje respecto al origen

5 Caso III
Comprobamos la condición cinemática de rigidez. Para el par AB
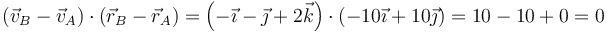
Para el AC
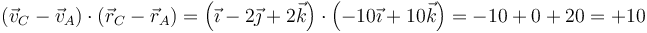
Puesto que esta cantidad no es nula, no necesitamos seguir. Este caso es incompatible con la condición de rigidez y por tanto no corresponde a un posible movimiento de un sólido rígido.
6 Caso IV
Este caso es el más sencillo de todos. Puesto que las velocidad de los tres puntos es la misma, el movimiento es una traslación, con velocidad (en cm/s)

7 Caso V
Como en el resto de los casos comprobamos la condición de rigidez. Para el par AB
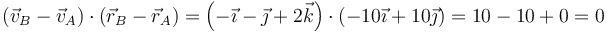
Para el AC

Para el BC
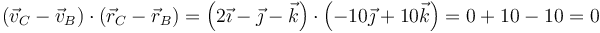
En los tres casos se satisface la condición. Por tanto, este es un posible movimiento de un sólido rígido.
Lo anterior es un copia-pega del caso I, ya que las diferencias son idénticas en todos los casos.
Calculamos la velocidad angular empleando el teorema de Chasles y el resultado es de nuevo el mismo que en el caso I.

Una vez que tenemos la velocidad angular, hallamos la velocidad de deslizamiento, a partir de la velocidad de cualquiera de los puntos
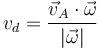
que nos da
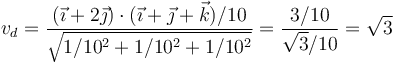
Puesto que esta velocidad no es nula, el movimiento es ahora helicoidal. La velocidad de deslizamiento, en forma vectorial, se escribe
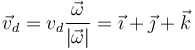
8 Caso VI
Comprobamos en primer lugar la condición de rigidez.
Entre A y B es automático, puesto que tienen la misma velocidad, por lo que su velocidad relativa es nula y no se alejan el uno del otro.
Para A y C tenemos

Para el BC
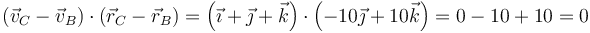
Por tanto se trata de un movimiento rígido.
Puesto que la velocidad de uno de los puntos es nula y la de otro no, el movimiento es una rotación. El eje instantáneo de rotación pasa por el punto de velocidad nula (en este caso el C).
Además los puntos A y B tienen la misma velocidad. Esto quiere decir que se encuentran sobre una recta paralela al EIR. Puesto que la dirección del eje la marca la velocidad angular, esto nos da la dirección de ésta.
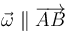
Hallamos el vector unitario en esta dirección
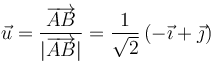
lo que nos permite escribir la velocidad angular como
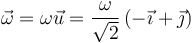
Para hallar el valor de la cantidad escalar ω aplicamos el teorema de Chasles

lo que nos da
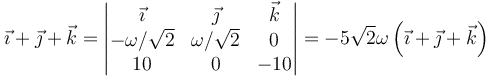
Por tanto
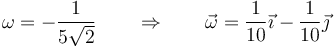
El EIR según hemos indicado, pasa por C y tiene la dirección de  , por lo que puede escribirse
, por lo que puede escribirse
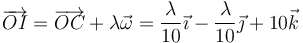
9 Resumen
Reuniendo los seis casos, tenemos la tabla
| Caso | Tipo |
|---|---|
| I | Rotación |
| II | Helicoidal |
| III | Imposible |
| IV | Traslación |
| V | Helicoidal |
| VI | Rotación |





