Problemas de herramientas matemáticas (GIOI)
De Laplace
(→Ángulo entre diagonales) |
(→Determinación de un vector a partir de sus proyecciones) |
||
| Línea 68: | Línea 68: | ||
<center><math>\vec{A}\cdot\vec{X}=k\qquad \vec{A}\times\vec{X} = \vec{C}</math></center> | <center><math>\vec{A}\cdot\vec{X}=k\qquad \vec{A}\times\vec{X} = \vec{C}</math></center> | ||
| - | Determine el valor de <math>\vec{X}</math>. ¿Es suficiente una sola de las dos ecuaciones para | + | Determine el valor de <math>\vec{X}</math>. ¿Es suficiente una sola de las dos ecuaciones para hallarlo</math>? |
[[Determinación de un vector a partir de sus proyecciones|Solución]] | [[Determinación de un vector a partir de sus proyecciones|Solución]] | ||
Revisión de 16:29 7 oct 2019
Contenido |
1 Arco capaz
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores 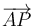 y
y
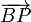 son ortogonales.
son ortogonales.
Inversamente, sean A, B y P tres puntos tales que 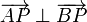 . Pruebe que el centro de la circunferencia que pasa por A, B y P se encuentra en el punto medio del segmento AB.
. Pruebe que el centro de la circunferencia que pasa por A, B y P se encuentra en el punto medio del segmento AB.
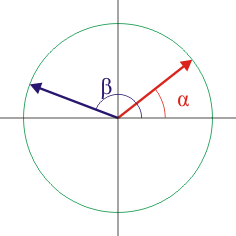
2 Coseno y seno de una diferencia
A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos.
3 Teoremas del seno y del coseno
Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno
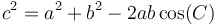
y del seno
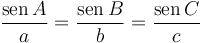
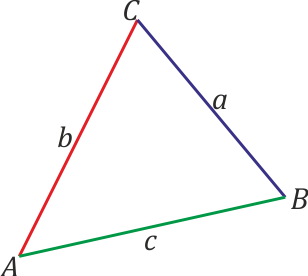
en un triángulo de lados a, b y c, y ángulos opuestos A, B y C.
4 Construcción de una base
Dados los vectores

Construya una base ortonormal dextrógira 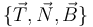 , tal que
, tal que
- El primer vector,
 , vaya en la dirección y sentido de
, vaya en la dirección y sentido de 
- El segundo,
 , esté contenido en el plano definido por
, esté contenido en el plano definido por  y
y  y apunte hacia el mismo semiplano (respecto de
y apunte hacia el mismo semiplano (respecto de  ) que el vector
) que el vector  .
.
- El tercero,
 , sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
, sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
- Supongamos un vector que en la base canónica se escribe
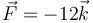
- ¿Cuál es su expresión en la base
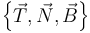
- ¿Cuál es su expresión en la base
5 Ejemplo de operaciones con dos vectores
Dados los vectores

- ¿Qué ángulo forman estos dos vectores?
- ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
- Escriba
 como suma de dos vectores, uno paralelo a
como suma de dos vectores, uno paralelo a  y otro ortogonal a él.
y otro ortogonal a él.
6 Ángulo entre diagonales
Calcule el ángulo que forman dos diagonales de un cubo.
7 Determinación de un vector a partir de sus proyecciones
Se tiene un vector conocido, no nulo,  y uno que se desea determinar,
y uno que se desea determinar, 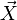 . Se dan como datos su producto escalar y su producto vectorial por
. Se dan como datos su producto escalar y su producto vectorial por 

Determine el valor de 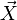 . ¿Es suficiente una sola de las dos ecuaciones para hallarlo</math>?
. ¿Es suficiente una sola de las dos ecuaciones para hallarlo</math>?





