Problemas de Gas Ideal
De Laplace
(→Expansión adibática no cuasiestáica) |
|||
| Línea 58: | Línea 58: | ||
== [[Comparación de un proceso isotérmico y uno adiabático]] == | == [[Comparación de un proceso isotérmico y uno adiabático]] == | ||
| - | |||
Un gas ideal monoatómico ocupa un volumen de <math>4\,\mathrm{m^3}</math> | Un gas ideal monoatómico ocupa un volumen de <math>4\,\mathrm{m^3}</math> | ||
a la presión de <math>8\,\mathrm{atm}</math> y a la temperatura de | a la presión de <math>8\,\mathrm{atm}</math> y a la temperatura de | ||
| Línea 68: | Línea 67: | ||
#Expansión isoterma. | #Expansión isoterma. | ||
#Expansión adiabática. | #Expansión adiabática. | ||
| - | |||
| - | |||
== [[Proceso isotermo y adiabático consecutivos]] == | == [[Proceso isotermo y adiabático consecutivos]] == | ||
Revisión de 19:27 27 abr 2009
1 Ecuación de estado
Utilizando la ecuación de estado de los gases ideales, responda a las siguientes preguntas
- ¿Que volumen ocupa un mol de gas en condiciones estándar?
- ¿Cuantas moléculas hay en
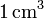de gas ideal a una temperatura de 300 K y a una presión de 1 atm?
¿Y si la presión es de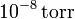 
?
2 Pistón oscilante
Un cilindro de 2.4 m de altura se llena con 0.1 moles de un gas ideal a una temperatura y presión normales. El cilindro se cierra entonces con un pistón de masa 1.4 kg que se deja caer hasta alcanzar el equilibrio.
- Determine la altura h0 del pistón suponiendo que la temperatura del gas no varía en la compresión.
- Suponga que el pistón se empuja ligeramente hacia abajo más allá de la posición de equilibrio y luego se libera. Suponiendo que la temperatura del gas permanece constante y que el rozamiento del pistón es despreciable, demuestre que el pistón describe un movimiento armónico simple y determine su frecuencia.
3 Trabajo en distintos procesos
Un mol de un gas ideal está contenido en un cilindro que tiene un émbolo móvil. La presión, volumen y temperatura iniciales son Pi,Vi,Ti, respectivamente. Calcule el trabajo realizado sobre el gas para los siguientes procesos, y dibuje cada uno de ellos en un diagrama PV
- Una compresión isobárica en la que el volumen final sea la mitad del volumen inicial
- Una compresión isotérmica en la que la presión final se cuatro veces la inicial
- Un proceso isócoro en el que la presión final sea el triple de la inicial.
4 Trabajo en un ciclo
Las condiciones iniciales del estado de un gas perfecto son: V=4 l, P=2 atm, t = 27o C. Se dilata el gas a presión constante hasta duplicar su volumen. A continuación se comprime isotérmicamente hasta recuperar el volumen inicial. Finalmente se enfría a volumen constante hasta su presión inicial.
- Dibuje el ciclo en un diagrama PV.
- Calcule el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos.
5 Trabajo en una y en dos etapas
Un gas diatómico se comprime adiabáticamente, de modo cuasiestático, desde 1 atm hasta 25 atm, siendo la temperatura inicial t = 25 °C. La compresión puede realizarse en una sola etapa o bien en dos: desde 1 atm hasta 5 atm primero, y desde 5 atm hasta 25 atm después, dejando que el gas se enfríe a presión constante hasta volver a su temperatura inicial entre las dos etapas.
- Dibuje los dos procesos en el diagrama PV .
- Determine cual de los dos procesos exige realizar un menor trabajo sobre el sistema.
Nota: No es necesario incluir el proceso intermedio de compresión a presión constante en el balance del trabajo realizado.
6 Comparación de un proceso isotérmico y uno adiabático
Un gas ideal monoatómico ocupa un volumen de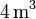 
a la presión de 
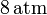y a la temperatura de
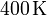. El gas se expande hasta la presión final de
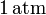mediante un proceso cuasiestático. Calcule el
trabajo realizado, el calor absorbido y la variación de energía interna en
los siguientes casos:
- Expansión isoterma.
- Expansión adiabática.
7 Proceso isotermo y adiabático consecutivos
Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar su presión inicial. Ambos procesos son cuasiestáticos. Halle
- La temperatura final
- El trabajo total realizado por el gas
- El calor total absorbido por el gas
- La variación de energía interna
8 Expansión adibática no cuasiestática
4 moles de nitrógeno están a 25 oC y 30 atm. Se pasa bruscamente la presión hasta un valor de 10 atm mediante una expansión adiabática del gas contra una presión exterior constante de 10 atm. El proceso no es cuasiestático. Calcule
- La temperatura final del gas suponiendo que la ecuación de estado de los gases ideales es aplicable a los estados inicial y final.
- La variación de energía interna.
- El trabajo realizado sobre el gas.
- Compare con las mismas magnitudes en un proceso adiabático cuasiestático que expanda el gas hasta la misma presión final de 10 atm.
