Trabajo en una y en dos etapas

De Laplace

1 Enunciado

Un gas diatómico se comprime adiabáticamente, de modo cuasiestático, desde 1 atm hasta 25 atm, siendo la temperatura inicial t = 25 °C. La compresión puede realizarse en una sola etapa o bien en dos: desde 1 atm hasta 5 atm primero, y desde 5 atm hasta 25 atm después, dejando que el gas se enfríe a presión constante hasta volver a su temperatura inicial entre las dos etapas.

Dibuje los dos procesos en el diagrama PV .
Determine cual de los dos procesos exige realizar un menor trabajo sobre el sistema.

Nota: No es necesario incluir el proceso intermedio de compresión a presión constante en el balance del trabajo realizado.

2 Introducción

Este problema pretende introducir algunos aspectos de la irreversibilidad que presenta los procesos termodinámicos reales. Para ello comparamos dos procesos con algunas características comunes:

En el primer proceso comprimimos un gas ideal de forma adiabática desde 1 a 25 atm. Esto correspondería a tener un cilindro con un pistón y a que presionáramos el pistón de forma lo suficientemente rápida como para que al gas no le de tiempo a intercambiar calor con el ambiente. En este caso todo el trabajo que realizamos sobre el sistema se invertirá en aumentar la energía interna.

En el segundo proceso, partimos del mismo estado inicial y subimos de nuevo hasta 25 atm pero en lugar de realizar la compresión de una vez, paramos a descansar cuando vamos por 5&atm;. Durante el periodo de descanso, al gas le da tiempo a enfriarse y volver a la temperatura inicial, que es la del ambiente. Esto lo hace cediendo calor y reduciendo la energía interna. Cuando volvemos a comprimir lo hacemos sobre un gas más frio que en el primer proceso, por lo que el trabajo del segundo paso será diferente.

En el balance de trabajo no incluiremos el trabajo del paso intermedio de enfriamiento porque "ocurre solo", esto es, se trata de un proceso espontáneo en el que el sistema cede calor al ambiente, y como tal irreversible. Al agente que está comprimiendo el pistón le basta con mantener la presión en este proceso.

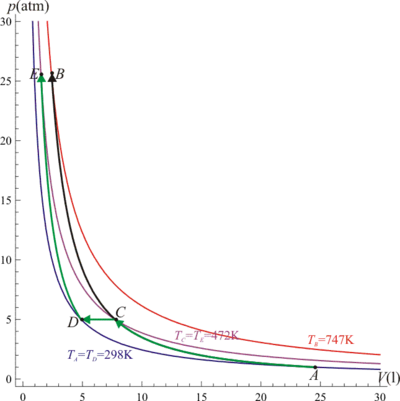
3 Diagrama PV

En un diagrama PV los dos procesos se representan de la forma siguiente:

La compresión adiabática en un solo paso corresponde a la curva negra en la figura, que va de A a B. Esta curva parte del punto A, que está a 298 K y 1 atm y va cortando isotermas, lo que corresponde a que el gas se calienta, hasta que llega al punto B, situado, como veremos, a una presión de 25 atm y una temperatura de 747 K.

La compresión en dos etapas se compone de tres tramos. El primero sigue a la curva anterior hasta el punto C, situado a una presión de 5 atm y una temperatura de 472 K. A partir de ahí el gas se enfría, manteniéndose la presión constante. El punto final de este paso intermedio es D, situado de nuevo a 298 K. A partir de ahí se produce la nueva compresión adiabática, que lleva al sistema al punto E, a 25 atm y a una temperatura de 472 K.

El trabajo en cada uno de los caminos corresponde al área situada bajo la curva y el eje de abscisas.

4 Trabajo realizado sobre el sistema

4.1 En una sola etapa

Consideremos el proceso adiabático que lleva del estado inicial A al final, B.

En un proceso adiabático el sistema no intercambia calor con el ambiente. De acuerdo con el primer principio de la termodinámica, el incremento en la energía interna se debe exclusivamente al trabajo realizado sobre el sistema. A su vez, la energía interna de un gas ideal depende exclusivamente de su temperatura, por lo que

$W_{A\to B} = \Delta U = n\,c_V\,\Delta T = n\,c_V(T_B-T_A)$

Sustituyendo la ecuación de estado de los gases ideales

$W_{A\to B} = \frac{c_V}{R}(p_BV_B-p_AV_A)=\frac{p_BV_B-p_AV_A}{\gamma-1}$

(donde hemos usado la ley de Mayer, $R = c p - c V = c V (γ - 1)$ ).

En esta expresión conocemos la presión inicial, $p A$ y la final $p B$ . El volumen inicial lo podemos hallar como

$V_A=\frac{nRT_A}{p_A}$

El volumen final lo hallamos observando que el proceso es adiabático y reversible y por tanto se cumple lay de Poisson

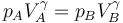
$p_AV_A^\gamma = p_BV_B^\gamma\,$ $\Rightarrow$ $V_B = V_A\left(\frac{p_A}{p_B}\right)^{\frac{1}{\gamma}}$

Sustituyendo esto en la expresión del trabajo queda

$W_{A\to B}=\frac{V_A}{\gamma-1}\left(p_B\left(\frac{p_A}{p_B}\right)^{\frac{1}{\gamma}}-p_A\right)=\frac{p_AV_A}{\gamma-1}\left(\left(\frac{p_B}{p_A}\right)^{\frac{\gamma-1}{\gamma}}-1\right)=\frac{nRT_A}{\gamma-1}\left(r_{AB}^{(\gamma-1)/\gamma}-1\right)$

donde llamamos $r A B = p B / p A$ a la relación de presión entre el estado final y el inicial. En ete proceso esta relación vale 25.

4.2 En dos etapas

Consideramos ahora el camino quebrado de A a E, con una compresión adiabática de A a C, un enfriamiento isóbaro de C a D y otra compresión adiabática de D a E.

4.2.1 Primera etapa

En el paso de A a C el cálculo del trabajo es completamente análogo al caso de la compresión adiabática de A a B. El trabajo resultante vale

$W_{A\to C}=\frac{nRT_A}{\gamma-1}\left(r_{AC}^{(\gamma-1)/\gamma}-1\right)$

con $r A C = p C / p A = 5$ en este caso.

4.2.2 Segunda etapa

En la segunda compresión adiabática, el cálculo es idéntico a los dos anteriores

$W_{D\to E}=\frac{nRT_D}{\gamma-1}\left(r_{DE}^{(\gamma-1)/\gamma}-1\right)=\frac{nRT_A}{\gamma-1}\left(r_{DE}^{(\gamma-1)/\gamma}-1\right)$

donde en el último paso se ha aplicado que el sistema se ha enfriado hasta volver a la temperatura inicial y $T D = T A$ . Puesto que la relación de presión $r D E = p E / p D = 5$ , este trabajo tiene exactamente el mismo valor numérico que el de A a C, esto es que pasar de 5 a 25 atm requiere el mismo trabajo que ir de 1 a 5, pese a que es el cuádruple de incremento en la presión.

4.2.3 El proceso intermedio

El trabajo que no hemos incluido es el de la compresión isóbara de C a D. El trabajo que se realiza sobre el sistema en este paso es

$W_{C\to D} = -p\,\Delta V = p_C(V_C-V_D)\,$

Sustituyendo la ley de Poisson y la ecuación de estado

$W_{C\to D} = p_CV_A\left(\frac{p_A}{p_C}\right)^{\frac{1}{\gamma}}-p_DV_D=nRT_A\left(r_{AC}^{(\gamma-1)/\gamma}-1\right)$

4.2.4 Trabajo total

Sumando el trabajo de las dos compresiones adiabáticas

$W_T=W_{A\to C}+W_{D\to E}=\frac{nRT_A}{\gamma-1}\left(r_{AC}^{(\gamma-1)/\gamma}+r_{DE}^{(\gamma-1)/\gamma}-2\right)$

5 Comparación entre los dos trabajos

Para ver cuál de los dos procesos requiere más trabajo dividimos el segundo por el primero y nos queda

$\frac{W_T}{W_{A\to B}}= \frac{r_{AC}^{(\gamma-1)/\gamma}+r_{DE}^{(\gamma-1)/\gamma}-2}{r_{AB}^{(\gamma-1)/\gamma}-1}$

En este caso, si llamamos simplemente $r$ a $r A B$ tenemos, según el enunciado

$r = r_{AB}=25\,$ $r_{AC}=r_{DE}=\sqrt{r}=5\,$ $\gamma=\frac{7}{5}=1.4\,$

obtenemos la proporción

$\frac{W_T}{W_{A\to B}}= \frac{2(r^{(\gamma-1)/2\gamma}-1)}{r^{(\gamma-1)/\gamma}-1}= 0.774$

es decir, que por el segundo camino realizamos un 22% menos de trabajo que por el primero. Al dejar que el sistema se enfríe, el segundo paso requiere menos trabajo que si lo hacemos todo de una vez.

5.1 El límite de infinitos pasos intermedios

Podemos imaginarnos más de dos pasos sucesivos, dejando que el sistema vuelva a la temperatura original. Si N, el número de pasos se hace tender a infinito, con cada paso manteniendo en cada uno la misma relación de presiones, la proporción entre el trabajo por pasos y el de una tacada tiende a

$\frac{W_T}{W_{A\to B}}=\lim_{N\to\infty}\frac{N(r^{(\gamma-1)/N\gamma}-1)}{r^{(\gamma-1)/\gamma}-1}=\frac{\ln(r^{(\gamma-1)/\gamma})}{r^{(\gamma-1)/\gamma}-1}$

que para $r = 25$ da

$\frac{W_T}{W_{A\to B}}\to 0.61$

un 39% menos de trabajo por la línea quebrada que por la adiabática.

6 Valores numéricos

Para ayudar a fijar ideas, vamos a calcular valores numéricos de las distintas magnitudes implicadas en los diferentes procesos. Para ello supondremos 1 mol de gas ideal, situado inicialmente a una presión inicial de 1 atm y a una temperatura de 298 K.

El volumen ocupado inicialmente por este gas es

$V_A = \frac{nRT_A}{p_A}= \frac{1\,\mathrm{mol}\times 0.082\,\mathrm{atm}\cdot\mathrm{l}/\mathrm{K}\cdot\mathrm{mol}\times 298\,\mathrm{K}}{1\,\mathrm{atm}} = 24.45\,\mathrm{l}$

6.1 En una etapa

En la compresión adiabática en una etapa, el volumen final es

$V_B = V_A\left(\frac{p_A}{p_B}\right)^{\frac{1}{\gamma}}=24.45\,\mathrm{l} \left(\frac{1}{25}\right)^{\frac{1}{1.4}}=2.45\,\mathrm{l}$

El volumen se reduce a una décima parte del original en esta compresión.

La temperatura en el estado final es

$T_B = \frac{p_BV_B}{nR} = 747.5\,\mathrm{K}$

El trabajo necesario para comprimir el gas es

$W_{A\to B} = \frac{p_BV_B-p_AV_A}{\gamma-1} = 92.2\,\mathrm{atm}\cdot\mathrm{l}=9.345\,\mathrm{kJ}$

6.2 En dos etapas

6.2.1 Primera compresión

En la compresión a 5 atm el volumen se reduce a

$V_C = V_A\left(\frac{p_A}{p_C}\right)^{\frac{1}{\gamma}}=7.75\,\mathrm{l}$

y la temperatura sube a

$T_C = \frac{p_CV_C}{nR} = 472.0,\mathrm{K}$

El trabajo para esta compresión

$W_{A\to C} = \frac{p_CV_C-p_AV_A}{\gamma-1} = 35.7\,\mathrm{atm}\cdot\mathrm{l}=3.616\,\mathrm{kJ}$

6.2.2 Enfriamiento isóbaro

Cuando el sistema se enfría su temperatura baja a $T_D=T_A=298\,\mathrm{K}$ , lo que conlleva una reducción adicional del volumen a

$V_D = \frac{n R T_D}{p_D}=\frac{n R T_A}{p_C}=4.89\,\mathrm{l}$

El trabajo que se realiza espontáneamente en este proceso es

$W_{C\to D}=p_C(V_C-V_D)=14.3\,\mathrm{atm}\cdot\mathrm{l}=1.447\,\mathrm{kJ}$

6.2.3 Segunda compresión

En la compresión de 5 atm a 25 atm el volumen se reduce a

$V_E = V_D\left(\frac{p_D}{p_E}\right)^{\frac{1}{\gamma}}=1.55\,\mathrm{l}$

y la temperatura sube a

$T_E = \frac{p_EV_E}{nR} = 472.0,\mathrm{K}$

esto es, volvemos a la temperatura del estado C.

El trabajo necesario para esta compresión

$W_{D\to E}= \frac{p_EV_E-p_DV_D}{\gamma-1}=35.7\,\mathrm{atm}\cdot\mathrm{l}=3.616\,\mathrm{kJ}$

Como dijimos en la solución analítica, los trabajos en las dos etapas son exactamente iguales.

6.2.4 Trabajo total

Sumando las dos compresiones adiabáticas

$W_T=W_{A\to C}+W_{D\to E}=71.4\,\mathrm{atm}\cdot\mathrm{l}=7.233\,\mathrm{kJ}$

6.3 Comparación entre los dos procesos

Dividiendo el trabajo del proceso en dos etapas por el de una sola llegamos a la proporción

$\frac{W_T}{W_{A\to B}} = \frac{71.4\,\mathrm{atm}\cdot\mathrm{l}}{92.2\,\mathrm{atm}\cdot\mathrm{l}}=0.774$

que, por supuesto, coincide con lo que obtuvimos en la solución analítica.

Trabajo en una y en dos etapas

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Diagrama PV

4 Trabajo realizado sobre el sistema

4.1 En una sola etapa

4.2 En dos etapas

4.2.1 Primera etapa

4.2.2 Segunda etapa

4.2.3 El proceso intermedio

4.2.4 Trabajo total

5 Comparación entre los dos trabajos

5.1 El límite de infinitos pasos intermedios

6 Valores numéricos

6.1 En una etapa

6.2 En dos etapas

6.2.1 Primera compresión

6.2.2 Enfriamiento isóbaro

6.2.3 Segunda compresión

6.2.4 Trabajo total

6.3 Comparación entre los dos procesos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES