Coordenadas cilíndricas. Diferenciales
De Laplace
(Diferencias entre revisiones)
(→Diferenciales de superficie) |
(→Diferencial de volumen) |
||
| Línea 20: | Línea 20: | ||
==Diferencial de volumen== | ==Diferencial de volumen== | ||
| + | Combinando los tres diferenciales | ||
| + | |||
| + | <center><math>\mathrm{d}\tau = \rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathrm{d}z</math></center> | ||
==Enlaces== | ==Enlaces== | ||
Revisión de 20:15 22 nov 2007
Contenido |
1 Diferencial de camino
Aplicando la expresión general del diferencial de camino resulta
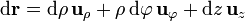
2 Diferenciales de superficie
Dependiendo de la coordenada que consideremos constante, tenemos tres vectores diferenciales de superficie:
- Superficie ρ = cte (cilindros rectos)
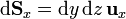
- Superficie
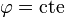 (semiplanos verticales)
(semiplanos verticales)
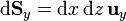
- Superficie z = cte (planos horizontales)

3 Diferencial de volumen
Combinando los tres diferenciales
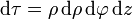
4 Enlaces
- Siguiente: Coordenadas esféricas. Diferenciales
- Anterior: Coordenadas cartesianas. Diferenciales





