Entrar Página Discusión Historial Go to the site toolbox

Diferenciales

De Laplace

Contenido

1 Introducción

Una de las operaciones que más a menudo se efectúan sobre los campos es la integración: sobre una línea, una superficie o un volumen y tanto integrales escalares como vectoriales.

Lo que nunca hay que perder de vista es que una integral es una suma de cosas muy pequeñitas. No tiene más misterio. Por ejemplo, si nos encontramos la integral

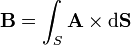
\mathbf{B} = \int_S \mathbf{A}\times\mathrm{d}\mathbf{S}

esto quiere decir simplemente que, dada una superficie 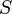S\,, la descomponemos en elementos diferenciales 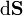\mathrm{d}\mathbf{S}\,. Cada uno de esos vectores elementales se multiplica vectorialmente por el vector \mathbf{A} y se suman todos esos productos. Como la suma de vectores es un vector, el resultado de la integral será una cantidad vectorial. Y eso es todo. No hay que quebrarse la cabeza meditando si es un flujo o una circulación, si hay que poner tal o cual jacobiano, o si podemos hallar una primitiva. Solo hay que sumar.

Eso sí, para poder sumar, primero debemos poder expresar correctamente los diferenciales de línea, de superficie o de volumen. Y su expresión dependerá del sistema de coordenadas que estemos empleando. Vamos a ello.


2 Diferencial de camino

Los factores de escala dan la proporcionalidad entre a variación en una coordenada y la distancia recorrida a lo largo de una línea coordenadas. Si variamos infinitesimalmente la coordenada $q_1$ recorremos la distancia

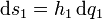
\mathrm{d}{s_1} = h_1 \,\mathrm{d}{q_1}

A esta distancia le corresponde un desplazamiento en la dirección de la línea coordenada de q1

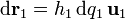
\mathrm{d}{\mathbf{r}_1} = h_1\,\mathrm{d}{q_1}\,\mathbf{u}_{1}

En el caso de que tengamos un desplazamiento general, en el cual cambien las tres coordenadas, el resultado será la suma vectorial (no la suma escalar de las distancias) de los desplazamientos individuales

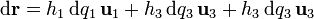
\mathrm{d}{\mathbf{r}}=h_1\,\mathrm{d}{q_1}\,\mathbf{u}_{1} + h_3\,\mathrm{d}{q_3}\,\mathbf{u}_{3} + h_3\,\mathrm{d}{q_3}\,\mathbf{u}_{3}

3 Diferencial de superficie

El diferencial de superficie escalar, dS es el área de un pequeño trocito de una superficie. Sin embargo, de bastante más interés es el diferencial vectorial, que se define como el producto de dicha área por el vector normal a la superficie

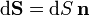
\mathrm{d}{\mathbf{S}} = \mathrm{d}{S}\,\mathbf{n}

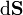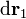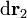Para obtener el vector \mathrm{d}{\mathbf{S}} consideramos dos vectores tangentes a la superficie \mathrm{d}{\mathbf{r}_1} y \mathrm{d}{\mathbf{r}_2}. El producto vectorial de estos dos vectores es otro vector...

  • Perpendicular a ambos vectores, esto es, perpendicular a la superficie.
  • De módulo igual al área del paralelogramo definido por ambos vectores.

pero estas dos propiedades son justamente las que definen el vector 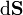\mathrm{d}{\mathbf{S}}. Por tanto,

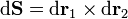
\mathrm{d}{\mathbf{S}} = \mathrm{d}{\mathbf{r}_1}\times\mathrm{d}{\mathbf{r}_2}

Esta construcción se puede hacer de forma general para cualquier superficie. Sin embargo, aquí nos limitaremos a considerar superficies coordenadas. ¿Por qué? Porque es más fácil y porque casi siempre trabajaremos con este tipo de superficies (ya que precisamente las superficies son las que nos inclinan a elegir un sistema de coordenadas u otro).

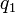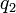Para una superficie q3 = cte los puntos de la superficie dependen de las coordenadas q_1\, y q_2\,, por lo que los dos diferenciales tangentes a la superficie son

\mathrm{d}\mathbf{r}_1 = h_1\,\mathrm{d}{q_1}\,\mathbf{u}_{1} \qquad \mathrm{d}\mathbf{r}_2 = h_2\,\mathrm{d}{q_2}\,\mathbf{u}_{2}

y el vector diferencial de superficie

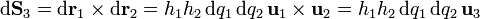
\mathrm{d}{\mathbf{S}}_3 = \mathrm{d}\mathbf{r}_1\times\mathrm{d}\mathbf{r}_2 = h_1h_2\,\mathrm{d}{q_1}\,\mathrm{d}{q_2}\,\mathbf{u}_{1}\times\mathbf{u}_{2} = h_1h_2\,\mathrm{d}{q_1}\,\mathrm{d}{q_2}\,\mathbf{u}_{3}

donde hemos aplicado que se trata de una base ortonormal dextrógira, en la que

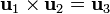
\mathbf{u}_{1}\times\mathbf{u}_{2}=\mathbf{u}_{3}

4 Diferencial de volumen

Un elemento de volumen, dτ es una pequeña porción del espacio. En principio, su forma es arbitraria. De hecho, a menudo es útil pensar en elementos esféricos. Sin embargo, por su simplicidad, consideraremos elementos en forma de paralelepípedo. Si tenemos tres diferenciales de camino no coplanarios, el volumen del prisma que determinan es

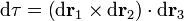
\mathrm{d}\tau = \left(\mathrm{d}\mathbf{r}_1\times\mathrm{d}\mathbf{r}_2\right)\cdot\mathrm{d}\mathbf{r}_3

considerando de nuevo diferenciales a lo largo de las líneas coordenadas y aplicando la ortonormalidad de las bases, esta expresión se reduce a

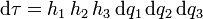
\mathrm{d}\tau = h_1\,h_2\,h_3\,\mathrm{d}{q_1}\,\mathrm{d}{q_2}\,\mathrm{d}{q_3}

4.1 ¿Qué pasó con el jacobiano?

Una de las cosas que se aprenden en Cálculo es que, para hacer una integral de volumen, hay que introducir una cantidad llamada jacobiano, de forma que

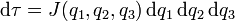
\mathrm{d}{\tau}=J(q_1,q_2,q_3)\,\mathrm{d}{q_1}\,\mathrm{d}{q_2}\,\mathrm{d}{q_3}

siendo

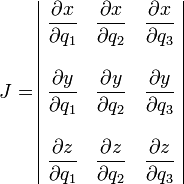
J = \begin{array}{|ccc|} \displaystyle\frac{\partial x}{\partial q_1} & \displaystyle\frac{\partial x}{\partial q_2} & \displaystyle\frac{\partial x}{\partial q_3} \\ & & \\\displaystyle\frac{\partial y}{\partial q_1} & \displaystyle\frac{\partial y}{\partial q_2} & \displaystyle\frac{\partial y}{\partial q_3} \\ & & \\\displaystyle\frac{\partial z}{\partial q_1} & \displaystyle\frac{\partial z}{\partial q_2} & \displaystyle\frac{\partial z}{\partial q_3}\end{array}

en la formula anterior para dτ parece que no hay tal jacobiano, pero por supuesto que está ahí. Simplemente ocurre que en un sistema de coordenadas ortogonales

J(q_1,q_2,q_3)=h_1h_2h_3\,

5 Enlaces

Obtenido de "http://tesla.us.es/wiki/index.php/Diferenciales"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 18:42, 13 abr 2010. - Esta página ha sido visitada 31.594 veces. - Aviso legal - Acerca de Laplace