Coordenadas cilíndricas. Diferenciales
De Laplace
Contenido |
1 Diferencial de camino
Aplicando la expresión general del diferencial de camino resulta
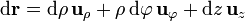
2 Diferenciales de superficie
Dependiendo de la coordenada que consideremos constante, tenemos tres vectores diferenciales de superficie:
- Superficie ρ = cte (cilindros rectos)
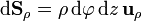
- Superficie
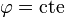 (semiplanos verticales)
(semiplanos verticales)
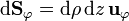
- Superficie z = cte (planos horizontales)
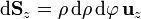
3 Diferencial de volumen
Combinando los tres diferenciales
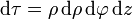
4 Enlaces
- Siguiente: Coordenadas esféricas. Diferenciales
- Anterior: Coordenadas cartesianas. Diferenciales





