Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del movimiento rectilíneo (GIE)

De Laplace

(Diferencias entre revisiones)
(→integración aproximada de la velocidad)
Línea 130: Línea 130:
<center><math>v = \frac{14.4t}{(t+2)^2}</math></center>
<center><math>v = \frac{14.4t}{(t+2)^2}</math></center>
-
: ¿Cuál es el error relativo cometido en el apartado anterior?
+
:: ¿Cuál es el error relativo cometido en el apartado anterior?
-
# Con ayuda de la cuadrícula halle el valor aproximado de la aceleración en <math>t = 3\,\mathrm{s}</math>. Calcule el valor exacto y el error cometido con la aproximación.
+
<ol start="3">
-
 
+
<li> Con ayuda de la cuadrícula halle el valor aproximado de la aceleración en <math>t = 3\,\mathrm{s}</math>. Calcule el valor exacto y el error cometido con la aproximación.</li>
 +
</ol>
==[[Calculo gráfico de velocidad media]]==
==[[Calculo gráfico de velocidad media]]==

Revisión de 10:12 8 oct 2012

Contenido

1 Persecución policial

Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado?

Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor?

2 Aproximación numérica de la velocidad y la aceleración

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
x (m) 0.00 -0.04 -0.06 -0.06 -0.04 0.00 0.06 0.14 0.24 0.36 0.50
  1. ¿En qué momento es máxima la velocidad? ¿En qué momento es nula? Calcule aproximadamente la velocidad en el intervalo entre t=0\,\mathrm{s} y t=1\,\mathrm{s}.
  2. Calcule aproximadamente la aceleración en el mismo intervalo.

3 Ejemplo de movimiento rectilíneo no uniforme

Una partícula se mueve a lo largo de una recta de forma que su posición sigue la ley, en el SI

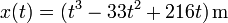
x(t) = (t^3-33t^2+216t)\,\mathrm{m}

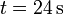entre t=0\,\mathrm{s} y t=24\,\mathrm{s}.

  1. Calcule la velocidad y la aceleración de este movimiento.
  2. ¿Cuál es la máxima distancia de la posición inicial a la que llega a encontrarse la partícula? ¿Cuánto vale el desplazamiento neto a lo largo del intervalo? ¿Y la distancia total recorrida?
  3. ¿Cuánto valen la máxima y la mínima rapidez de este movimiento?

4 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

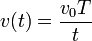
v(t) = \frac{v_0T}{t}

¿Cuánto vale la velocidad media entre t = T y t = 3T?

5 Ejemplos de velocidad en función de la posición

1) La velocidad de una partícula sigue la ley

v = \sqrt{Ax}

siendo x la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

2) Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

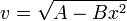
v = \sqrt{A- B x^2}

con A y B constantes positivas.

  1. ¿En que se medirá B en el SI?
  2. ¿Cómo depende de la posición la aceleración de la partícula?

6 Velocidad decreciente con la posición

Mediante una serie de sensores se mide la velocidad de un vehículo en puntos equiespaciados, obteniéndose la tabla

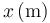
x\,(\mathrm{m}) 0.0 100.0 200.0 300.0 400.0 500.0
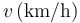
v\,(\mathrm{km}/\mathrm{h}) 108 90 72 54 36 18
  1. ¿Qué ley sencilla cumple la velocidad como función de la posición?
  2. Determine la aceleración como función de x. ¿Se trata de un movimiento uniformemente acelerado?
  3. Halle el valor de la aceleración en cada uno de los puntos de medida.
  4. Calcule el tiempo empleado en recorrer los 500 m. Si continúa con este movimiento, ¿cuánto tardará en recorrer 600 m?

7 Frenado de un fórmula 1

Cuando el Ferrari de Fernando Alonso se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 340 km/h. Cuando entra en la chicane va a 80 km/h.

  1. Suponiendo que la aceleración es constante, determine su valor.
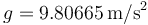  2. Exprese el resultado en el SI y como un múltiplo de g (siendo g=9.80665\,\mathrm{m}/\mathrm{s}^2).
  3. Determine la velocidad como función de la posición y represéntela gráficamente.

8 integración aproximada de la velocidad

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

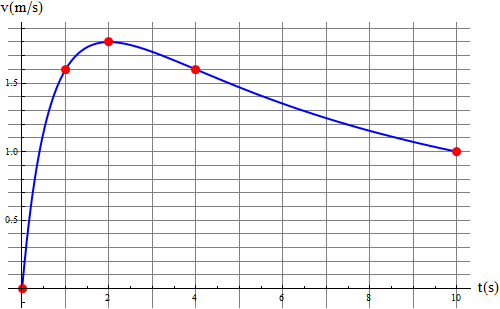
Archivo:graf-vt.png

La partícula parte de x = 0.

  1. Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en t=10\,\mathrm{s}.
  2. Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad, en el SI, es
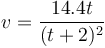
v = \frac{14.4t}{(t+2)^2}
¿Cuál es el error relativo cometido en el apartado anterior?
  1. Con ayuda de la cuadrícula halle el valor aproximado de la aceleración en 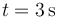t = 3\,\mathrm{s}. Calcule el valor exacto y el error cometido con la aproximación.

9 Calculo gráfico de velocidad media

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

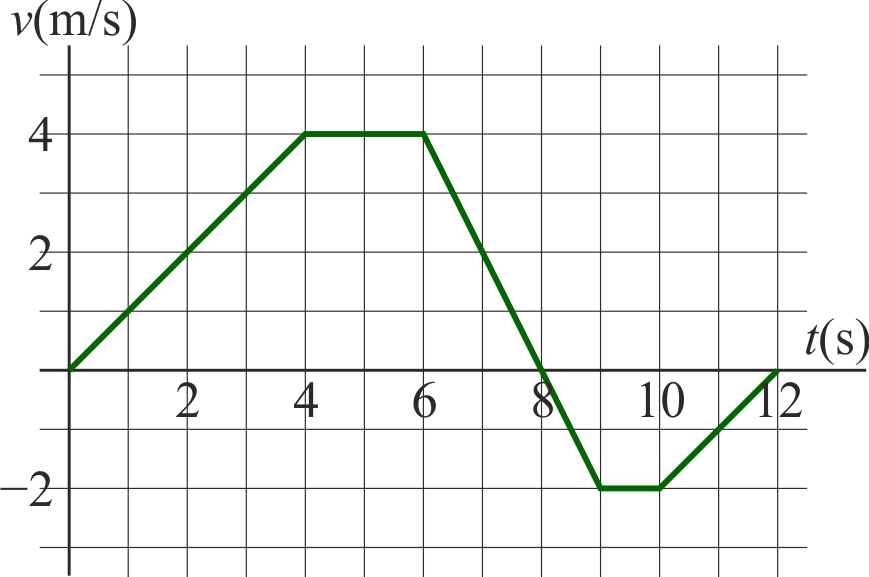
Archivo:velocidad-quebrada.png
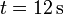  1. ¿Cuánto vale aproximadamente la velocidad media entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?
  2. ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?

10 Movimiento sinusoidal cuadrático

Una partícula oscila según la ley

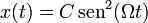
x(t) = C\,\mathrm{sen}^2(\Omega t)
  1. Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
  2. ¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

11 Ejemplo de integración numérica

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

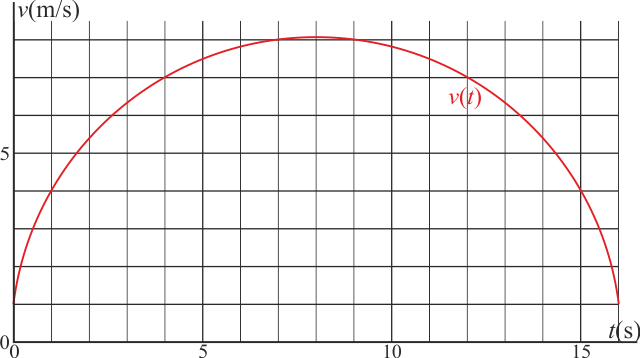
Archivo:velocidad-circulo.png

La partícula parte de s = 0.

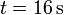  1. Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en t=16\,\mathrm{s}.
  2. Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es
v = \sqrt{1+16t-t^2}
¿Cuál es el error relativo cometido en el apartado anterior?
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_movimiento_rectil%C3%ADneo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace