Problemas de introducción a la termodinámica (GIE)
De Laplace
(→Variación de la presión de los neumáticos) |
(→Termómetro de gas con resorte) |
||
| Línea 56: | Línea 56: | ||
<li>Si queremos construir una escala para los grados Celsius con este termómetro, ¿estarán las líneas equiespaciadas?</li> | <li>Si queremos construir una escala para los grados Celsius con este termómetro, ¿estarán las líneas equiespaciadas?</li> | ||
</ol> | </ol> | ||
| - | [[Categoría:Problemas del principio cero de la termodinámica (GIE)]] | + | |
| + | <center>[[Archivo:termometro-gas-resorte.png]]</center> | ||
| + | |||
| + | [[Categoría:Problemas del principio cero de la termodinámica (GIE)|0]] | ||
Revisión de 09:51 14 feb 2012
Contenido |
1 Conversión entre escalas de temperaturas
Exprese las siguientes temperaturas en la escala Celsius, absoluta y Fahrenheit:
- Cero absoluto
- 0°F
- 100°F
- Punto triple del agua
- Punto de fusión del azufre a 1 atm
- Punto de sublimación del hielo seco a 1 atm
2 Dilatación de una esfera metálica
Se tiene una bola hueca de hierro que a 20°C tiene un radio interior de 12.0 mm y un radio exterior de 15.0 mm, siendo la densidad del hierro a esta temperatura 7874 kg/m³ y su coeficiente de dilatación lineal 11.8×10−6K−1.
Se eleva la temperatura de la bola a 50°C. Determine:
- Los nuevos radios interior y exterior de la bola.
- La densidad del hierro a 50°C.
- El incremento en el volumen ocupado por el hierro.
- Si la bola de hierro está llena de aire que inicialmente tiene una presión de 100 kPa, ¿cuál será la presión del gas cuando la esfera está a 50°C?
3 Variación de la densidad del agua
La densidad del agua a 0°C vale 999.8395 kg/m³ a 4°C vale 999.9720 kg/m³ y a 10°C vale 999.7026 kg/m\³. Determine aproximadamente el coeficiente de dilatación volumétrico a estas tres temperaturas.
4 Análisis de termómetro de mercurio
Se construye un termómetro empleando un capilar de 0.4 mm de diámetro en el que hay una columna de mercurio que a 0°C mide 2.0 cm. Suponiendo que el coeficiente de dilatación lineal vale 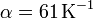 en el intervalo (0°C,100°C) y despreciando la dilatación del vidrio,
¿cuánto mediría la columna a 100°C si el mercurio fuera sólido? ¿Cu´anto mide, teniendo en cuenta que es líquido? ¿Es esto suficiente para hacerlo legible?
en el intervalo (0°C,100°C) y despreciando la dilatación del vidrio,
¿cuánto mediría la columna a 100°C si el mercurio fuera sólido? ¿Cu´anto mide, teniendo en cuenta que es líquido? ¿Es esto suficiente para hacerlo legible?
Suponga ahora que en el extremo inferior del capilar hay una pequeña esfera que contiene 0.5 cm³ de mercurio, ¿cuánto medirá en ese caso la columna de mercurio a 100°C?
5 Compresión isoterma de un gas
Un cilindro vertical de 10.0 cm de diámetro contiene hidrógeno a 25°C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura. Se coloca sobre la tapa una pesa de 2.0 kg. Halle la altura de la tapa una vez que se alcanza de nuevo el equilibrio térmico con el exterior. ¿A qué temperatura habrá que calentar el gas para que la tapa vuelva a su posición inicial, con el peso todavía encima?
6 Tubo con dos cámaras de gas
Se tiene una cámara cilíndrica horizontal de 20 cm de diámetro y 60 cm de longitud de paredes rígidas. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente está fijado con pernos. En la cámara de la izquierda hay 4.0 g de H2 gaseoso y en la de la derecha 4.0 g de N2. Los dos gases y el ambiente que los rodea están a 25°C.
- Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central.
- Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas
7 Variación de la presión de los neumáticos
Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la tempera exterior es de 5°C. Si no los toca en seis meses y no hay fugas, ¿cuál será la presión manométrica un día de julio a 40°C? ¿Qué proporción de aire debe extraer de cada neumático para devolver la presión a 2.4 bar? Si tras reducir la presión se despreocupa otros seis meses, ¿cuál será la presión manométrica cuando vuelva a hacer 5°C? Desprecie la dilatación de los neumáticos.
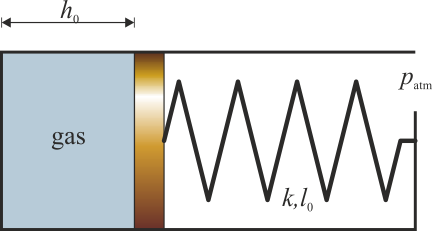
8 Termómetro de gas con resorte
Se construye un termómetro de gas mediante un cilindro de sección S en el interior del cual hay un pistón que puede deslizarse sin rozamiento. El pistón cierra una cámara en la que hay un gas ideal. La cara exterior del pistón está unida al extremo del tubo mediante un resorte de constante k y longitud natural l0. Esta parte del tubo está abierta a la atmósfera. Para un cierto valor de la temperatura, t0, la presión es la atmosférica, el pistón se encuentra a una distancia h0 del fondo y el resorte no ejerce fuerza alguna. Cuando el gas se calienta, se expande y el resorte se comprime.
- Determine la temperatura del gas cuando el resorte se encuentra comprimido una distancia x.
- Indique cómo sería en un diagrama pV la curva correspondiente a un aumento cuasiestático de la temperatura entre T0 y T1.
Suponga que el diámetro del cilindro es 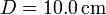 , la presión exterior
, la presión exterior 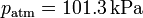 , la altura del pistón a
, la altura del pistón a 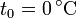 es
es 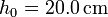 y a
y a 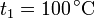 es
es 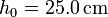 .
.
- Calcule la constante del resorte.
- Determine la posición del pistón cuando
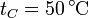
- Si queremos construir una escala para los grados Celsius con este termómetro, ¿estarán las líneas equiespaciadas?