Entrar Página Discusión Historial Go to the site toolbox

Problemas de Dinámica del punto (GIC)

De Laplace

(Diferencias entre revisiones)
(→Partícula en un tubo que gira con velocidad angular constante)
(→Partícula en un pozo de potencial)
Línea 70: Línea 70:
#Sabiendo que la partícula inicia su movimiento desde el reposo en el punto <math>P_0</math> de coordenada <math>x=2L</math>, determina su energía mecánica.
#Sabiendo que la partícula inicia su movimiento desde el reposo en el punto <math>P_0</math> de coordenada <math>x=2L</math>, determina su energía mecánica.
#¿En qué otro punto (de la región <math>x<L</math>) la partícula se detiene momentáneamente (punto de retorno)? ¿Cuánto tiempo emplea en llegar desde <math>x=L</math> a ese punto de retorno?
#¿En qué otro punto (de la región <math>x<L</math>) la partícula se detiene momentáneamente (punto de retorno)? ¿Cuánto tiempo emplea en llegar desde <math>x=L</math> a ese punto de retorno?
 +
 +
==[[Partícula deslizando sobre un disco (GIA) |Partícula deslizando sobre un disco]]==
 +
[[Imagen:F1_GIA_masa_resbalando_sobre_disco_enunciado.png|right]]
 +
Una partícula <math>P</math>, de masa <math>m</math>, es abandonada en reposo en el punto más alto de un disco vertical de radio <math>R</math> que descansa apoyado en el suelo. Debido a una ligera perturbación, la partícula comienza a deslizar bajo la acción de la gravedad. Suponiendo que no hay rozamiento, determina el punto en el que la partícula pierde contacto con el disco, así como la velocidad con la que impacta contra el suelo.

Revisión de 13:22 30 nov 2011

Contenido

1 Equilibrio de una partícula bajo la acción de tres muelles

Una partícula libre de masa m está unida a tres muelles de longitud natural nula y constantes elásticas kA, kB y kC. Cada uno de los muelle tiene el otro extremo fijado en un punto. Las coordenadas de los puntos de fijación son A( − a,0,0), B(a,0,0) y C(0,a,0).

  1. Calcula la posición de equilibrio de la partícula.
  2. Considera las situaciones siguientes
    1. m = 0 y kA = kB = kC = k
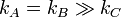
    2. m = 0 y k_A=k_B\gg k_C
    3. kA = kB = kC = k y m > > ka / g.

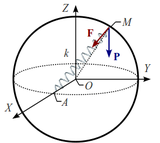
2 Equilibrio de una partícula sobre una esfera lisa

Un punto material M de peso P está obligado a permanecer en la superficie de una esfera de radio R y centro O. Además, M es atraído por un punto fijo A del ecuador de la superficie esférica, debido a la existencia de un resorte elástico ideal, de longitud natural nula y de constante recuperadora 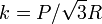k=P/\sqrt{3}R, que conecta ambos puntos. Determina las posiciones de equilibrio del punto material M, y la fuerza de reacción vincular en ellas.


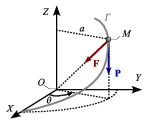
3 Equilibrio de una partícula sobre una hélice

Un punto material M, de peso P, está vinculado a la hélice Γ, definida en el sistema de referencia cartesiano OXYZ por la ecuación vectorial 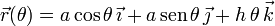\vec{r}(\theta)=a\cos\theta\,\vec{\imath}+a\,\mathrm{sen}\,\theta\,\vec{\jmath}+h\,\theta\,\vec{k}. Determina la posición de equilibrio estático del punto M si, además, este es atraído por el origen por una fuerza \vec{F} proporcional a la distancia entre ambos puntos, siendo k la constante de proporcionalidad.

4 Fuerza unidireccional

Una partícula de masa m está sometida a una fuerza constante 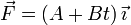\vec{F}=(A + Bt)\,\vec{\imath}. Si parte del reposo y desde el origen del sistema de referencia, encuentra la posición y la velocidad de la partícula en cualquier instante.

5 Partícula en el campo gravitatorio terrestre

Una partícula de masa m se mueve en el seno del campo gravitatorio terrestre cerca de la superficie, de modo que la aceleración de la gravedad puede suponerse constante y dirigida verticalmente a la superficie (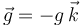\vec{g}=-g\,\vec{k}). Analiza el movimiento de la partícula para las siguientes condiciones iniciales

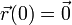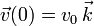  1. \vec{r}(0)=\vec{0}, \vec{v}(0)=v_0\,\vec{k}.
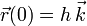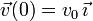  2. \vec{r}(0)=h\,\vec{k}, \vec{v}(0)=v_0\,\vec{\imath}.
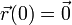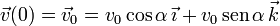  3. \vec{r}(0)=\vec{0}, \vec{v}(0)=\vec{v}_0=v_0\cos\alpha\,\vec{\imath} + v_0\,\mathrm{sen}\,\alpha\,\vec{k}.

6 Muelle vertical

Se tiene un muelle vertical de constante K y longitud natural l0. El sistema está sometido a la acción de la gravedad, 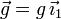\vec{g}=g\,\vec{\imath}_1.

  1. Se cuelga una masa m del extremo del muelle. ¿Cuál es la nueva elongación del muelle cuando se alcanza el equilibrio?
  2. Partiendo de la situación del apartado anterior, estiramos la masa de modo que la elongación del muelle aumenta una distancia L, y lo soltamos. Describe las fuerzas actuando sobre la masa justo después de soltarla.
  3. Aplicando la Segunda Ley de Newton calcula la posición de la masa como función del tiempo. ¿Que movimiento describe?

Nota : Podemos suponer que todos los desplazamientos del muelle son verticales.

7 Partícula ensartada en un aro circular

Se tiene un aro circular de radio R. Engarzado en él hay una masa m que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad.

  1. Suponiendo que el contacto es liso, encuentra las ecuaciones que describen el movimiento de la masa en función del ángulo α de la figura.
  2. Soltamos la masa con velocidad inicial nula y un ángulo inicial 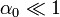\alpha_0\ll1. Encuentra la función α(t) que describe el movimiento de la masa.
  3. Supongamos ahora que nos dicen que la masa realiza un movimiento circular uniforme con frecuencia angular Ω. Encuentra la expresión de la fuerza de ligadura en función del ángulo θ. ¿Es constante? En este caso, ¿el vínculo es liso o rugoso?

8 Partícula en un tubo que gira con velocidad angular constante

Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme ω en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede describirse como

\begin{matrix} x(t) = r(t)\,\cos(\omega t)&\qquad\qquad& y(t) = r(t)\,\,\mathrm{sen}\,(\omega t) \end{matrix}
  1. Halla la ecuación diferencial que cumple la función r(t) sabiendo que el vínculo entre la partícula y el tubo es liso.
  2. Comprueba que
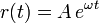
r(t) = A\,e^{\omega t}

es una solución de la ecuación para r(t).

  1. Para esta solución particular
    1. Calcula la fuerza ejercida por el tubo en cada instante.
    2. Halla la potencia desarrollada por el tubo sobre la partícula. Calcula el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de r = b a r = 2b.
    3. Calcula el incremento de la energía cinética de la partícula en el mismo intervalo y comprueba que se verifica el teorema de las fuerzas vivas o de la energía.

9 Partícula en un pozo de potencial

Una partícula P, de masa m, realiza un movimiento rectilíneo sobre la parte positiva del eje OX. La partícula está sometida a una fuerza que tiene la forma

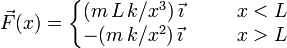
\vec{F}(x) = \left\{ \begin{matrix} (m\,L\,k/x^3)\,\vec{\imath}&\quad&x< L\\ -(m\,k/x^2)\,\vec{\imath}&\quad&x>L \end{matrix} \right.

siendo k una constante conocida.

  1. Determina la energía potencial de la partícula en función de su coordenada x (considerando que es nula en el infinito y exigiendo su continuidad en x = L) y represéntala gráficamente.
  2. Sabiendo que la partícula inicia su movimiento desde el reposo en el punto P0 de coordenada x = 2L, determina su energía mecánica.
  3. ¿En qué otro punto (de la región x < L) la partícula se detiene momentáneamente (punto de retorno)? ¿Cuánto tiempo emplea en llegar desde x = L a ese punto de retorno?

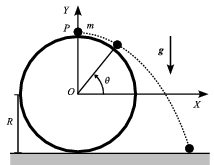
10 Partícula deslizando sobre un disco

Una partícula P, de masa m, es abandonada en reposo en el punto más alto de un disco vertical de radio R que descansa apoyado en el suelo. Debido a una ligera perturbación, la partícula comienza a deslizar bajo la acción de la gravedad. Suponiendo que no hay rozamiento, determina el punto en el que la partícula pierde contacto con el disco, así como la velocidad con la que impacta contra el suelo.

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_Din%C3%A1mica_del_punto_(GIC)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace