Entrar Página Discusión Historial Go to the site toolbox

Partícula en un tubo que gira con velocidad angular constante (GIA)

De Laplace

Contenido

1 Enunciado

Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme ω en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede describirse como

\begin{matrix} x(t) = r(t)\,\cos(\omega t)&\qquad\qquad& y(t) = r(t)\,\,\mathrm{sen}\,(\omega t) \end{matrix}
  1. Halla la ecuación diferencial que cumple la función r(t) sabiendo que el vínculo entre la partícula y el tubo es liso.
  2. Comprueba que
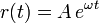
r(t) = A\,e^{\omega t}

es una solución de la ecuación para r(t).

  1. Para esta solución particular
    1. Calcula la fuerza ejercida por el tubo en cada instante.
    2. Halla la potencia desarrollada por el tubo sobre la partícula. Calcula el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de r = b a r = 2b.
    3. Calcula el incremento de la energía cinética de la partícula en el mismo intervalo u comprueba que se verifica el teorema de las fuerzas vivas o de la energía.

2 Solución

2.1 Ecuaciones de movimiento

La ecuación de movimiento es la Segunda Ley de Newton

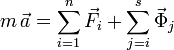
m\,\vec{a} = \sum\limits_{i=1}^n\vec{F}_i + \sum\limits_{j=i}^s\vec{\Phi}_j

donde 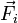\vec{F}_i son las fuerzas activas y 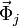\vec{\Phi}_j son las fuerzas de reacción vincular que actúan sobre las partículas.

En este problema no hay fuerzas activas, pues no se habla del peso. La única fuerza que actúa sobre la partícula es la fuerza de reacción vincular, \vec{\Phi} , que ejerce sobre ella el tubo cuando gira, obligándola a permanecer dentro de él. El enunciado dice que el vínculo es liso. Esto quiere decir que \vec{\Phi} es perpendicular al tubo. Por tanto la segunda Ley de Newton queda

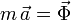
m\,\vec{a} = \vec{\Phi}


Vamos a resolver el problema usando coordenadas polares. En estas coordenadas los vectores de posición, velocidad y aceleración son

\begin{array}{l} \vec{r} = \rho\,\vec{u}_{\rho} \\ \\ \vec{v} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta} \\ \\ \vec{a} = (\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta})\,\vec{u}_{\theta} \end{array}

Artículo completo: Coordenadas polares

En este problema la partícula está obligada a permanecer dentro del tubo, y este gira con velocidad angular constante ω. Por tanto, la variación del ángulo θ con el tiempo es

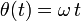
\theta(t) = \omega\,t

Hemos tomado θ(0) = 0 para simplificar. Por tanto, en este caso las expresiones de la posición, la velocidad y la aceleración quedan

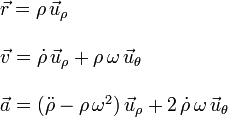
\begin{array}{l} \vec{r} = \rho\,\vec{u}_{\rho} \\ \\ \vec{v} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\omega\,\vec{u}_{\theta} \\ \\ \vec{a} = (\ddot{\rho}-\rho\,\omega^2)\,\vec{u}_{\rho} + 2\,\dot{\rho}\,\omega\,\vec{u}_{\theta} \end{array}

La expresión de la fuerza de reacción vincular en coordenadas polares, al ser perpendicular al tubo, es

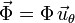
\vec{\Phi} = \Phi\,\vec{u}_{\theta}

La Segunda Ley de Newton, que es una ecuación vectorial, da lugar en este caso a dos ecuaciones escalares, una por cada componente

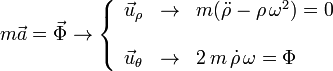
m\vec{a} = \vec{\Phi} \rightarrow \left\{ \begin{array}{lcl} \vec{u}_{\rho} & \to & m(\ddot{\rho}-\rho\,\omega^2)=0 \\ & & \\ \vec{u}_{\theta} & \to & 2\,m\,\dot{\rho}\,\omega = \Phi \end{array} \right.

Resolviendo la primera ecuación obtenemos ρ(t). Una vez conocida esta, la segunda ecuación nos da la expresión de la fuerza de reacción vincular Φ(t).

2.2 Resolución de la ecuación diferencial

2.2.1 Solución general

La ecuación diferencial para ρ(t) es

\ddot{\rho} = w^2\,\rho

Puede comprobarse que las funciones eωt y e − ωt son solución de esta ecuación. Por tanto, la solución general es de la forma

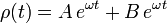
\rho(t) = A\,e^{\omega t} + B\,e^{\omega t}

Las constantes A y B se determinan a partir de las condiciones iniciales.

La solución general puede escribirse de una forma alternativa usando las definiciones del seno y coseno hiperbólicos

\cosh(\alpha) = \dfrac{e^{\alpha} + e^{-\alpha}}{2} \qquad\qquad \mathrm{senh}(\alpha) = \dfrac{e^{\alpha} - e^{-\alpha}}{2}

De esta forma la solución general se puede escribir

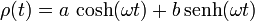
\rho(t) = a\,\cosh(\omega t) + b\,\mathrm{senh}(\omega t)

2.2.2 Condiciones iniciales

Vamos a suponer que en el instante inicial el tubo es paralelo al eje OX y la partícula está situada a una distancia ρ0 del origen. Eso nos da una condición inicial sobre la posición

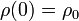
\rho(0) = \rho_0\,

Al empezar a girar el tubo, en un primer momento la partícula gira con él, por lo que la velocidad no tiene componente radial. Así pues,

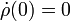
\dot{\rho}(0)=0

Determinamos las constantes a y b a partir de estas condiciones iniciales

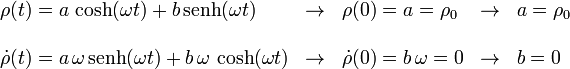
\begin{array}{lclcl} \rho(t) = a\,\cosh(\omega t) + b\,\mathrm{senh}(\omega t) &\to& \rho(0)=a=\rho_0 &\to& a = \rho_0 \\ &&&& \\ \dot{\rho}(t) = a\,\omega\,\mathrm{senh}(\omega t) + b\,\omega\,\cosh(\omega t) &\to& \dot{\rho}(0)=b\,\omega=0 &\to& b= 0 \end{array}

Así pues, la evolución en el tiempo de la posición de la partícula, expresada en coordenadas polares, viene dada por las funciones

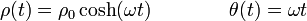
\rho(t) = \rho_0\cosh(\omega t) \qquad \qquad \theta(t) = \omega t

2.2.3 Comportamiento asintótico

La función que da la evolución de la distancia de la partícula al origen puede escribirse

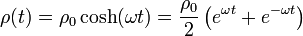
\rho(t) = \rho_0\cosh(\omega t) = \dfrac{\rho_0}{2}\left(e^{\omega t} + e^{-\omega t}\right)

Al aumentar el tiempo, la primera exponencial crece, mientras que la segunda decrece. Vamos a ver que en un tiempo corto esta segunda exponencial puede despreciarse respecto a la primera. La escala de tiempo relevante es el tiempo que tarda el tubo en dar una vuelta. Si la velocidad angular es ω este tiempo es

T = 2π / ω

Vamos a ver el valor de las exponenciales para algunos valores de t

Tiempo eωt e − ωt e − ωt / eωt
0 1 1 1
T/4 4.81 0.208 0.043
T/2 23.1 0.043 0.0019

Es decir, cuando el tubo ha dado simplemente media vuelta, el valor de la segunda exponencial es sólo un 0.19% del valor de la primera. Este factor se va haciendo más pequeño. Esto quiere decir que después de media vuelta del tubo, el valor de la coordenada ρ(t) puede aproximarse con muy buena aproximación por

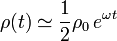
\rho(t) \simeq \dfrac{1}{2}\rho_0\,e^{\omega t}

2.3 Fuerza ejercida por el tubo

La ecuación obtenida de las componentes angulares de la Segunda Ley de Newton nos da el valor de la fuerza de reacción vincular

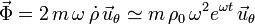
\vec{\Phi} = 2\,m\,\omega\,\dot{\rho}\,\vec{u}_{\theta}\simeq m\,\rho_0\,\omega^2e^{\omega t}\,\vec{u}_{\theta}

Hemos usado la aproximación asintótica de ρ(t).

2.4 Potencia desarrollada sobre la partícula

Dada una fuerza \vec{\Phi} actuando sobre una partícula, la potencia que le transfiere en cada instante es

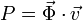
P = \vec{\Phi}\cdot\vec{v}

En nuestro caso, usando coordenadas polares tenemos

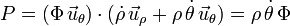
P = (\Phi\,\vec{u}_{\theta})\cdot(\dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta}) =\rho\,\dot{\theta}\,\Phi

En este problema, y utilizando la expresión asintótica de ρ(t) tenemos

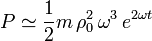
P \simeq \dfrac{1}{2}m\,\rho_0^2\,\omega^3\,e^{2\omega t}

2.5 Trabajo realizado sobre la partícula entre ρ = b y ρ = 2b

Vamos a calcular estre trabajo de dos formas, integrando la potencia en el tiempo e integrando el trabajo a partir de su definición

2.5.1 Integración de la potencia

La potencia instantánea se define como

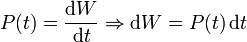
P(t) = \dfrac{\mathrm{d}W}{\mathrm{d}t} \Rightarrow \mathrm{d}W = P(t)\,\mathrm{d}t

Como tenemos la expresión de la potencia instantánea en función del tiempo, tenemos que hacer la integral

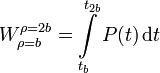
W_{\rho=b}^{\rho=2b} = \int\limits_{t_b}^{t_{2b}}P(t)\,\mathrm{d}t

donde tb y t2b son los instantes de tiempo en los cuales el valor de ρ(t) es b y 2b, respectivamente. Para determinar estos valores usamos la expresión asintótica de ρ(t)

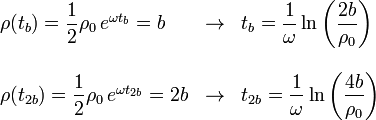
\begin{array}{lcl} \rho(t_b) = \dfrac{1}{2}\rho_0\,e^{\omega t_b}=b & \to & t_b = \dfrac{1}{\omega}\ln\left(\dfrac{2b}{\rho_0}\right) \\ \\ \rho(t_{2b}) = \dfrac{1}{2}\rho_0\,e^{\omega t_{2b}}=2b & \to & t_{2b} = \dfrac{1}{\omega}\ln\left(\dfrac{4b}{\rho_0}\right) \end{array}

Ahora podemos hacer la integral

\begin{array}{ll} W_{\rho=b}^{\rho=2b}& = \int\limits_{t_b}^{t_{2b}}P(t)\,\mathrm{d}t\\ &\\ & = \int\limits_{t_b}^{t_{2b}}\dfrac{1}{2}m\,\rho_0^2\,\omega^3\,e^{2\omega t}\,\mathrm{d}t\\ &\\ & = \dfrac{1}{2}m\,\rho_0^2\,\omega^3\int\limits_{t_b}^{t_{2b}}\,e^{2\omega t}\,\mathrm{d}t\\ &\\ & = \dfrac{1}{4}m\,\rho_0^2\,\omega^2\left[e^{2\omega t}\right]_{t_b}^{t_{2b}} \end{array}

Tenemos

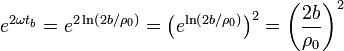
e^{2\omega t_b} = e^{2\ln\left(2b/\rho_0\right)} = \left(e^{\ln\left(2b/\rho_0\right)}\right)^2= \left(\dfrac{2b}{\rho_0}\right)^2

Operando igual para 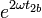e^{2\omega t_{2b}} obtenemos para el trabajo

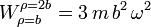
W_{\rho=b}^{\rho=2b} = 3\,m\,b^2\,\omega^2

2.5.2 Integración de la definición de trabajo

Al realizar un desplazamiento diferencial 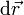\mathrm{d}\vec{r} el trabajo realizado por la fuerza de reacción vincular es

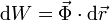
\mathrm{d}W = \vec{\Phi}\cdot\mathrm{d}\vec{r}

El desplazamiento 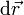\mathrm{d}\vec{r} es

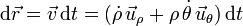
\mathrm{d}\vec{r} = \vec{v}\,\mathrm{d}t = (\dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta})\,\mathrm{d}t

Una derivada es un cociente entre dos incrementos muy pequeños. Podemos hacer entonces

\dot{\rho}\,\mathrm{d}t = \dfrac{\mathrm{d}\rho}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\rho \qquad\qquad \dot{\theta}\,\mathrm{d}t = \dfrac{\mathrm{d}\theta}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\theta

Entonces el desplazamiento diferencial se puede expresar en función de las variaciones infinitesimales de ρ y θ

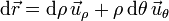
\mathrm{d}\vec{r} = \mathrm{d}\rho\,\vec{u}_{\rho} + \rho\,\mathrm{d}\theta\,\vec{u}_{\theta}

Entonces el trabajo realizado por la fuerza de reacción vincular en un tiempo dt es

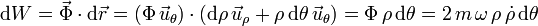
\mathrm{d}W = \vec{\Phi}\cdot\mathrm{d}\vec{r} = (\Phi\,\vec{u}_{\theta})\cdot(\mathrm{d}\rho\,\vec{u}_{\rho} + \rho\,\mathrm{d}\theta\,\vec{u}_{\theta}) = \Phi\,\rho\,\mathrm{d}\theta = 2\,m\,\omega\,\rho\,\dot{\rho}\,\mathrm{d}\theta

Utilizando otra vez la idea de que la derivada es un cociente tenemos

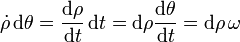
\dot{\rho}\,\mathrm{d}\theta = \dfrac{\mathrm{d}\rho}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\rho\dfrac{\mathrm{d}\theta}{\mathrm{d}t} = \mathrm{d}\rho\,\omega

Por tanto el trabajo infinitesimal es

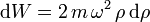
\mathrm{d}W = 2\,m\,\omega^2\,\rho\,\mathrm{d}\rho

Ahora podemos calcular el trabajo en función del cambio en la coordenada radial

W_{\rho=b}^{\rho=2b} = \int\limits_b^{2b}2\,m\,\omega^2\,\rho\,\mathrm{d}\rho= m\,\omega^2\,\left[\rho^2\right]_b^{2b} =3\,m\,b^2\,\omega^2

Obtenemos el mismo resultado que con el método anterior.

2.6 Variación de la energía cinética

La energía cinética en cada instante es

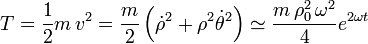
T = \dfrac{1}{2}m\,v^2 = \dfrac{m}{2}\left(\dot{\rho}^2+ \rho^2\dot{\theta}^2\right) \simeq \dfrac{m\,\rho_0^2\,\omega^2}{4}e^{2\omega t}

donde hemos usado la solución asintótica. Como tenemos los instantes de tiempo que corresponden a ρ = b y ρ = 2b, podemos calcular la variación de energía cinética

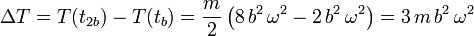
\Delta T = T(t_{2b}) - T(t_b) = \dfrac{m}{2}\left(8\,b^2\,\omega^2 - 2\,b^2\,\omega^2\right) = 3\,m\,b^2\,\omega^2

Podemos comprobar que la variación de la energía cinética es igual al trabajo realizado por la fuerza de reacción vincular. Se verifica así el teorema de las fuerzas vivas.

Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_en_un_tubo_que_gira_con_velocidad_angular_constante_(GIA)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 14:21, 28 nov 2010. - Esta página ha sido visitada 5.596 veces. - Aviso legal - Acerca de Laplace