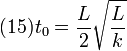Partícula en un pozo de potencial (GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una partícula $P$ , de masa $m$ , realiza un movimiento rectilíneo sobre la parte positiva del eje $O X$ . La partícula está sometida a una fuerza que tiene la forma

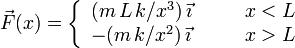
$\vec{F}(x) = \left\{ \begin{array}{lcl} (m\,L\,k/x^3)\,\vec{\imath}&\quad&x< L\\ -(m\,k/x^2)\,\vec{\imath}&\quad&x>L \end{array} \right.$

siendo $k$ una constante conocida.

Determina la energía potencial de la partícula en función de su coordenada $x$ (considerando que es nula en el infinito y exigiendo su continuidad en $x = L$ ) y represéntala gráficamente.
Sabiendo que la partícula inicia su movimiento desde el reposo en el punto $P 0$ de coordenada $x = 2 L$ , determina su energía mecánica.
¿En qué otro punto (de la región $x < L$ ) la partícula se detiene momentáneamente (punto de retorno)? ¿Cuánto tiempo emplea en llegar desde $x = L$ a ese punto de retorno?

2 Solución

En este problema no hay dos fuerzas , sino una sola fuerza cuya expresión es diferente según en que región del eje $O X$ nos encontremos. Para $x < L$ la fuerza es repulsiva, alejando a la partícula del origen. Para $x > L$ la fuerza es atractiva, atrayéndola hacia el origen.

Para determinar la energía potencial aplicamos su definición como trabajo realizado por la fuerza al trasladar la partícula. El problema nos dice que consideremos como origen de potenciales el infinito, donde la energía potencial es cero. Entonces, para un punto cualquiera del eje $O X$ la energía potencial vale

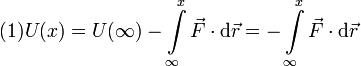
$(1) U(x) = U(\infty)-\int\limits_{\infty}^x\vec{F}\cdot\mathrm{d}\vec{r}=-\int\limits_{\infty}^x\vec{F}\cdot\mathrm{d}\vec{r}$

El vector $\mathrm{d}\vec{r}$ va siguiendo la curva que recorremos para venir desde el infinito hasta el punto sobre el eje de coordenada $x$ . Como en este caso nos movemos siempre sobre el eje $O X$ , la curva en cuestión es el propio eje, es decir

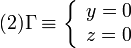
$(2) \Gamma\equiv \left\{ \begin{array}{l} y=0\\z=0 \end{array} \right.$

Por tanto, un desplazamiento elemental sobre el eje es

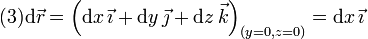
$(3) \mathrm{d}\vec{r}= \left(\mathrm{d} x\,\vec{\imath}+\mathrm{d} y\,\vec{\jmath}+\mathrm{d} z\,\vec{k}\right)_{(y=0,z=0)} = \mathrm{d} x\,\vec{\imath}$

Así pues, la energía potencial en un punto de coordenada $x$ es

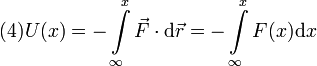
$(4) U(x) = -\int\limits_{\infty}^x\vec{F}\cdot\mathrm{d}\vec{r}=-\int\limits_{\infty}^xF(x)\mathrm{d} x$

A la hora de hacer esta integral, hay que fijarse en que la expresión de $F (x)$ depende del valor de $x$ . Debemos distinguir dos casos

\paragraph{ $x > L$ } Debemos usar la expresión de $F (x)$ para $x > L$ . Por tanto

$(5) U(x) = -\int\limits_{\infty}^x\left(-\frac{\displaystyle mk}{\displaystyle x^2}\right)\mathrm{d} x= mk\int\limits_{\infty}^x\frac{1}{x^2}\mathrm{d} x= -mk\left[\frac{1}{x}\right]_{\infty}^x= -\frac{mk}{x}$

\paragraph{ $x < L$ } En este caso, hay que dividir la integral en dos partes

$(6) \begin{array}{ll} U(x)&=-\int\limits_{\infty}^xF(x)\mathrm{d} x=-\int\limits_{\infty}^LF(x)\mathrm{d} x-\int\limits_{L}^xF(x)\mathrm{d} x = U(L) -\int\limits_{L}^x\frac{\displaystyle mkL}{\displaystyle x^3}\mathrm{d} x =\\ \\ & =-\frac{\displaystyle mk}{\displaystyle L}+mkL\left[\frac{\displaystyle 1}{\displaystyle 2x^2}\right]_L^x= \frac{\displaystyle mk}{\displaystyle 2L}\left(\frac{\displaystyle L^2}{\displaystyle x^2}-3\right) \end{array}$

Para calcular $U (L)$ hemos usado la expresión encontrada para $x > L$ . Imponemos así que la energía potencial sea continua a lo largo del eje.

Por tanto, la energía potencial para cualquier punto del eje $X$ es

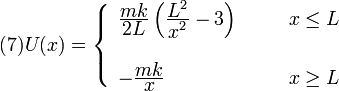
$(7) U(x) = \left\{ \begin{array}{lcl} \frac{\displaystyle mk}{\displaystyle 2L}\left(\frac{\displaystyle L^2}{\displaystyle x^2}-3\right) &\quad&x\leq L\\ &&\\ -\frac{\displaystyle mk}{\displaystyle x}&\quad&x\geq L \end{array} \right.$

La gráfica de la derecha muestra los valores de la energía potencial, mecánica y cinética para este caso. La energía mecánica es la línea horizontal constante. La energía potencial tiende a infinito cerca del origen y a cero al alejarse. La parte en $x < L$ representa la región con fuerza repulsiva mientras que en $x > L$ la fuerza es atractiva.

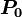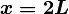
2.1 Partícula que parte del reposo en $\boldsymbol{P_0}$ con $\boldsymbol{x=2L}$

La energía mecánica de la partícula en cada instante es la suma de su energía cinética y su energía potencial. Esta suma se conserva durante el movimiento. Nos dicen que en el instante inicial está en reposo, es decir, su energía cinética es nula. Por tanto su energía mecánica es

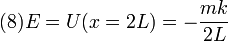
$(8) E = U(x=2L) = -\frac{\displaystyle mk}{\displaystyle 2L}$

2.2 Punto de retorno

La energía cinética en cada posición se calcula a partir de la conservación de la energía mecánica

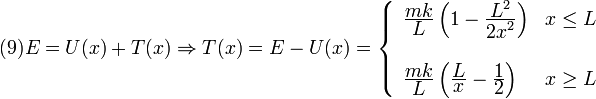
$(9) E = U(x)+T(x)\Rightarrow T(x) = E-U(x) = \left\{ \begin{array}{ll} \frac{\displaystyle mk}{\displaystyle L}\left(1-\frac{\displaystyle L^2}{\displaystyle 2x^2}\right)&x\leq L\\ &\\ \frac{\displaystyle mk}{\displaystyle L}\left(\frac{\displaystyle L}{\displaystyle x}-\frac{\displaystyle 1}{\displaystyle 2}\right)&x\geq L \end{array} \right.$

La gráfica muestra el valor de la energía cinética al variar $x$ . Ahora bien, $T$ debe ser siempre positiva, $T = m v 2 / 2$ , por tanto los valores de $x$ para los que $T$ es negativa no tienen sentido físico. En este caso, la partícula parte del punto de corte más a la derecha entre la energía mecánica y la energía potencial. No puede moverse hacia la derecha, pues entonces su energía cinética sería negativa (la fuerza en esta zona empuja hacia el origen). Se desplaza entonces hacia la izquierda acelerándose ( $T$ crece), hasta que $T$ llega a un máximo y empieza a disminuir (cuando entra en la región de fuerza repulsiva). Cuando $T = 0$ , su velocidad se hace cero (punto de retorno). Este punto se encuentra imponiendo la condición $T = 0$ en la zona de $x < L$ , es decir

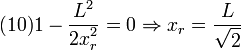
$(10) 1-\frac{\displaystyle L^2}{\displaystyle 2x_r^2}=0\Rightarrow x_r = \frac{\displaystyle L}{\displaystyle \sqrt{2}}$

2.3 Tiempo para ir de 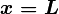$\boldsymbol{x=L}$ hasta el punto de retorno

Podemos calcular la velocidad a partir de la energía cinética. En la zona $x < L$ tenemos

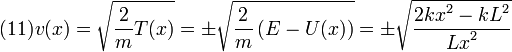
$(11) v(x) = \sqrt{\frac{\displaystyle 2}{\displaystyle m}T(x)}=\pm\sqrt{\frac{\displaystyle 2}{\displaystyle m}\left(E-U(x)\right)}= \pm\sqrt{\frac{\displaystyle 2kx^2-kL^2}{\displaystyle Lx^2}}$

Elegimos el signo menos pues en el caso que estamos examinando la partícula se desplaza hacia la izquierda. Por definición de velocidad, el tiempo que tarda la partícula en recorrer un espacio infinitesimal $d x$ es

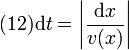
$(12) \mathrm{d} t = \left|\frac{\displaystyle \mathrm{d} x}{\displaystyle v(x)}\right|$

Consideramos el valor absoluto para no preocuparnos por el signo.

Entonces, el tiempo total que tarda en recorrer el espacio entre $x = L$ y 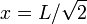$x=L/\sqrt{2}$ es la suma de todos los pequeños intervalos de tiempo, es decir

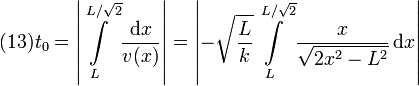
$(13) t_0 = \left|\int\limits_{L}^{L/\sqrt{2}}\frac{\displaystyle \mathrm{d} x}{\displaystyle v(x)}\right|= \left|-\sqrt{\frac{\displaystyle L}{\displaystyle k}}\int\limits_{L}^{L/\sqrt{2}}\frac{\displaystyle x}{\displaystyle \sqrt{2x^2-L^2}}\,\mathrm{d} x \right|$

Teniendo en cuenta que

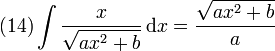
$(14) \int\frac{\displaystyle x}{\displaystyle \sqrt{ax^2+b}}\,\mathrm{d} x = \frac{\displaystyle \sqrt{ax^2+b}}{\displaystyle a}$

obtenemos que el tiempo pedido es

$(15) t_0 = \frac{\displaystyle L}{2}\sqrt{\displaystyle \frac{L}{k}}$

Partícula en un pozo de potencial (GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Partícula que parte del reposo en $\boldsymbol{P_0}$ con $\boldsymbol{x=2L}$

2.2 Punto de retorno

2.3 Tiempo para ir de $\boldsymbol{x=L}$ hasta el punto de retorno

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Partícula en un pozo de potencial (GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Partícula que parte del reposo en con

2.2 Punto de retorno

2.3 Tiempo para ir de hasta el punto de retorno

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.1 Partícula que parte del reposo en $\boldsymbol{P_0}$ con $\boldsymbol{x=2L}$

2.3 Tiempo para ir de $\boldsymbol{x=L}$ hasta el punto de retorno