Problemas de dinámica del sólido rígido (CMR)
De Laplace
1 Fuerza sobre una barra
Sobre una barra de longitud b y masa M situada en reposo horizontalmente en una superficie sin rozamiento se aplica una fuerza F0 también horizontal. El punto de la aplicación se encuentra a una distancia c del centro de la barra.
- Si la fuerza es perpendicular a la barra, ¿cuánto valen la aceleración del CM y la aceleración angular de la barra? ¿Alrededor de qué punto comienza a girar la barra?
- Suponga ahora que la fuerza forma un ángulo β con la barra, ¿cuánto valen ese caso las aceleraciones y donde se encuentra el centro instantáneo de rotación?
- Suponga que la barra se encuentra articulada en un extremo de forma que sólo puede girar en torno a este punto. ¿Cuánto valen las aceleraciones en ese caso? ¿Cuánto vale la fuerza que el punto de articulación ejerce sobre la barra?
- Si la barra estuviera empotrada en su extremo, de forma que no pudiera moverse de ninguna manera, ¿cuánto valdrían la fuerza y el momento de reacción ejercidos por la articulación?
2 Equilibrio de una barra apoyada
Supongamos que tenemos una barra de masa m y longitud 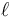 apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto.
apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto.
- Suponga primero que no hay rozamiento con las superficies y que la barra forma un ángulo θ con la pared. ¿Puede quedarse en equilibrio la barra para algún valor de θ?
- Suponga ahora que la barra posee un coeficiente de rozamiento estático μ con el suelo. ¿Para qué ángulos puede alcanzarse entonces el equilibrio?
- En una posición de equilibrio del apartado anterior, ¿cuánto valen las fuerzas de reacción norma-les en la pared y el suelo?

3 Movimiento de una barra apoyada
Suponga que la barra del problema anterior se encuentra apoyada sobre un suelo sin rozamiento y sobre la pared vertical. Inicialmente se encuentra vertical apoyada en la esquina pero una ligera sacudida hace que empiece a resbalar. Para el instante en que forma un ángulo θ con la pared, halle:
- La velocidad angular
 y la aceleración angular
y la aceleración angular 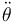 de la barra.
de la barra.
- Las fuerzas de reacción ejercidas por el suelo y la pared.
- Existe un valor de θ para el cual la barra se separa de la pared. Determine este valor.
- Halle la ecuación de movimiento para la barra una vez que se ha separado de la pared.
- Calcule el valor de θ ̇ en el momento en que la barra impacta con el suelo.
4 Motocicleta que acelera
Es conocido que al arrancar un coche, éste levanta un poco el morro y se hunde por la parte trasera. El mismo principio se aplica a los caballitos de las motocicletas. Supongamos una motocicleta con una masa M y tal que su centro de masas se encuentra a una altura H respecto a los ejes de las ruedas (las cuales tienen radio R, masa m y momento de inercia I). El CM está a una distancia dA del eje delantero y a una dB del trasero.
- Calcule la fuerza que se ejerce sobre cada eje cuando la moto arranca con una aceleración a0 sobre un suelo horizontal.
- Determine la fuerza de rozamiento que el suelo ejerce sobre cada rueda, así como el par ejercido por el motor sobre el eje de tracción (el de la rueda trasera).
- ¿Cuál es la aceleración máxima que puede alcanzar la moto sin que su rueda trasera patine?
- ¿Cuánto vale la potencia desarrollada por las diferentes fuerzas y momentos sobre el cuerpo y sobre las ruedas? ¿Cómo se transmite la energía aportada por el motor a las diferentes partes del sistema?
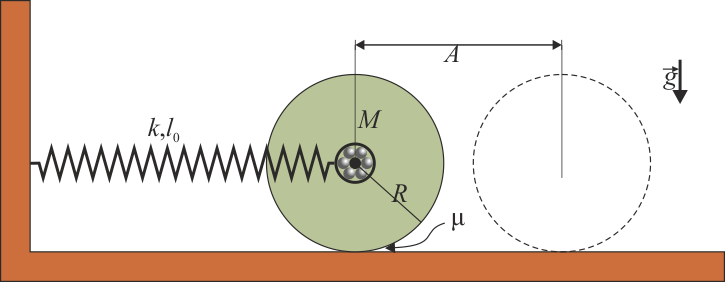
5 Rodillo unido a un resorte
Un rodillo cilíndrico macizo de radio R y masa M se encuentra apoyado sobre una superficie horizontal, siendo el coeficiente de rozamiento (estático y dinámico) μ. El eje del rodillo está atado a la pared mediante un resorte de constante k y longitud natural l0.
Se separa el rodillo de la posición de equilibrio una distancia A y se suelta desde el reposo. El rodillo rueda sin deslizar.
- Halle la velocidad del centro del rodillo y la velocidad angular para el instante en que su centro pasa por la posición de equilibrio.
- ¿Cuánto vale el periodo de las oscilaciones que describe?
- Calcule la fuerza de rozamiento estático que ejerce el suelo sobre el rodillo (a) en la posición inicial y (b) al pasar por la posición de equilibrio.
- ¿Cuál es el máximo valor de A que se puede alejar el rodillo si no se quiere que este empiece a deslizar sobre el suelo?
6 Motocicleta en una curva
A la hora de tomar una curva, ¿de qué sirve inclinarse lateralmente?
- Supongamos que Jorge Lorenzo toma una curva de 150 m de radio a una velocidad de 160 km/h ¿cuánto debe inclinarse en grados respecto a la vertical para no caerse ni a un lado ni al otro?
- Es sabido que Marc Márquez es capaz de inclinarse más que otros pilotos. Si en esa misma curva Márquez se inclina 60°, ¿a qué velocidad puede pasar por la curva? ¿Cuánto debe valer como mínimo el coeficiente rozamiento estático del neumático sobre el asfalto?
- Si en esa curva, Pedrosa intenta hacer lo mismo que Jorge y Marc, pero pisa un charco que nadie más ha visto, de forma que el coeficiente de rozamiento estático se reduce a μ = 0.5, ¿qué efecto tiene sobre la moto (a) respecto a su trayectoria (b) respecto a su inclinación?
7 |Péndulo Compuesto (I)
Se tiene un péndulo compuesto consistente en una barra homogénea de longitud 2b y masa m suspendida por un punto situado O a una distancia d del centro G de la barra (d < b).:
- Determine el periodo de oscilación de la barra si se suelta desde un ángulo pequeño θ0 respecto a la vertical.
- Suponga ahora que la barra se sitúa en el equilibrio inestable con el CM por encima del punto de apoyo y desde ahí se suelta con una velocidad inicial muy pequeña. Para el instante en que pasa por la vertical, calcule:
- La velocidad angular de la barra y la velocidad lineal de los extremos de la barra.
- Calcule la fuerza ejercida sobre el punto de anclaje.
- Calcule la tensión en cada punto de la barra.
- Repita los cálculos del apartado anterior para el momento en que forma un ángulo θ con la vertical.
8 Péndulo Compuesto (II)
Para el péndulo compuesto del problema anterior, considere que el soporte en O es una rótula, de forma que puede girar libremente alrededor de dicho punto. Si se hace girar la barra con la velocidad angular adecuada Ω alrededor del eje OZ1 es posible conseguir que mantenga un ángulo θ constante con la vertical.
Determine cuál debe ser el valor de Ω para un ángulo θ dado.
¿Es posible conseguir que se incline con ángulo constante para cualquier valor de Ω?
9 Péndulo Compuesto (III)
Para el sistema de los dos problemas anteriores (1 y 2) suponga ahora el caso general en el que la barra se mueve libremente, modificando el ángulo θ con la vertical y el ángulo φ alrededor del eje OZ1.
- Determine las ecuaciones de movimiento para estos dos ángulos.
- Halle dos constantes de movimiento no triviales.
- Con ayuda de las constantes anteriores, halle una ecuación de movimiento para θ que no incluya a φ
- Calcule qué valor debe tener la velocidad angular
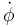 para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
10 Péndulo compuesto
Una barra homogénea de 1kg de masa y 1m de longitud está suspendida del techo por dos soportes muy ligeros, uno de ellos está articulado a un punto A, situado a 20cm de un extremo de la barra y el otro está articulado sin rozamiento en el otro extremo O.
- Determine la fuerza que ejerce cada soporte en el equilibrio.
- En un momento dado, se rompe el soporte en A. Justo tras el corte, halle:
- La aceleración lineal del centro de masas de la barra, G.
- La aceleración angular de la barra
- La fuerza que realiza el soporte en O. ¿Cuánto ha aumentado o disminuido respecto a la situación de equilibrio?
- Suponga que la articulación en O es un par de revolución, de forma que solo puede moverse en el plano OXZ
- Obtenga la ecuación de movimiento para el ángulo que forma con la vertical
- Halle las frecuencia de las pequeñas oscilaciones que realiza cuando se suelta desde una posición próxima a la vertical.
- Para el caso del enunciado, que se suelta desde la posición horizontal, calcule la fuerza que ejerce el soporte en O para cada ángulo θ
- Suponga ahora que la articulación en O es una rótula, de forma que la barra puede tanto variar su ángulo θ con la vertical como el ángulo φ alrededor de OZ.
- Determine las ecuaciones de movimiento para estos dos ángulos.
- Halle dos constantes de movimiento no triviales.
- Con ayuda de las constantes anteriores, halle una ecuación de movimiento para θ que no incluya a φ
- Calcule qué valor debe tener la velocidad angular
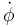 para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
11 Disco que rueda sobre corona
Un engranaje está formado por una cavidad circular de radio R (“sólido 1”) que se encuentra inmóvil y por cuyo perímetro interior rueda sin deslizar un disco homogéneo de masa m y radio r (sólido 2). Este disco está empujado por una varilla ideal sin masa cuyo extremo O está engranado a un eje de un motor y que está ranurada de manera que el disco 2 se halla ensartado son rozamiento en la ranura mediante un pequeño vástago de masa despreciable. Todo el sistema es horizontal por lo que no hace falta considerar el efecto del peso.

Considere un instante en el que el centro del disco se encuentra sobre el eje OY (ver figura). En ese instante la velocidad del centro G del disco 2 vale 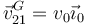 y su aceleración tangencial vale
y su aceleración tangencial vale 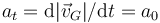 .
.
Para ese instante y empleando el sistema de ejes indicado en la figura (con OZ hacia afuera del papel), halle:
- El vector velocidad angular y el vector aceleración angular del disco 2, de radio r, respecto al 1.
- La aceleración del centro del disco 2 y la del punto A del disco 2 en contacto con el sólido 1.
- La energía cinética del disco 2, así como su momento cinético respecto a su centro y respecto al punto O, centro del sistema.
- Calcule las fuerzas que se ejercen sobre el disco 2 en su centro (por la varilla) y en el punto A.
- Halle el par que ejerce el motor en O para mantener el sistema en funcionamiento.
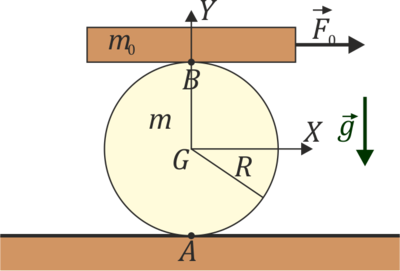
12 Plataforma sobre cilindro rodante
Un rodillo cilíndrico macizo homogéneo de masa m y radio R puede rodar sin deslizar sobre una superficie horizontal. El rodillo se encuentra impulsado por una fina plataforma horizontal de masa m0 cuyo contacto con el rodillo es también de rodadura sin deslizamiento. En un instante dado en que la plataforma está centrada sobre el rodillo y el sistema se halla en reposo se tira de ella con una fuerza 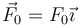 . Determine, en el orden que estime necesario:
. Determine, en el orden que estime necesario:
- La aceleración angular del rodillo, la aceleración del centro del rodillo, y la aceleración de la plataforma.
- Las fuerzas que actúan sobre el rodillo en el punto A, de contacto con el suelo y el punto B, donde se apoya la plataforma.
- Si el coeficiente de rozamiento estático entre el rodillo y el suelo, y entre el rodillo y la plataforma, vale μ, ¿cuál es valor máximo de F0 para que el rodillo no deslice? ¿Por dónde empezará a deslizar, por el punto A o por el punto B?
13 Rotores desequilibrados
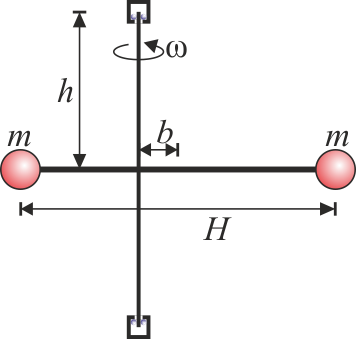
Se tiene un rotor formado por dos masas iguales, de valor m situadas en los extremos de una barra ideal (sin masa) de longitud H. Cuando este rotor está equilibrado gira en torno a un eje perpendicular a la barra y que pasa por su centro. Este eje está anclado en dos rodamientos situados a una distancia h del centro de la barra (uno por encima y otro por debajo de ella).
Calcule las fuerzas horizontales que el rotor produce sobre los rodamientos cuando gira con velocidad angular constante ω en torno al eje si:
- Es horizontal y se encuentra centrado en el eje vertical.
- Es horizontal pero se encuentra descentrado de forma que el eje no pasa por el centro de la barra, sino a una distancia b de éste.
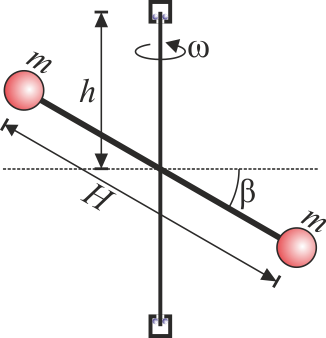
- Está centrado pero la barra está inclinada respecto a la horizontal un ángulo β.
- Es horizontal y se encuentra centrado en el eje vertical, pero las masas no son exactamente iguales, sino que vale m_1 y m_2.
Desprecie el efecto del peso.
14 Placa rectangular giratoria
Sabiendo que el momento de inercia de una chapa rectangular de masa m, base b y altura h respecto a un eje tangente a la chapa, paralelo a la base por su centro es IXX = mh2 / 12:
- Halle el tensor de inercia de una chapa de masa
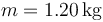 ,
, 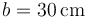 y
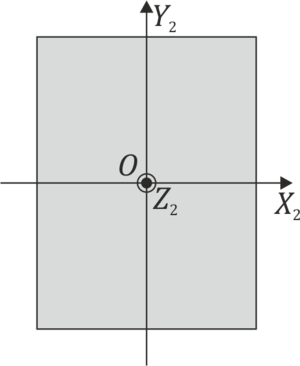
y 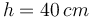 respecto a un triedro ortogonal cuyos ejes pasan por el centro de la chapa y OX2 y OY2 son paralelos a los lados.
respecto a un triedro ortogonal cuyos ejes pasan por el centro de la chapa y OX2 y OY2 son paralelos a los lados.
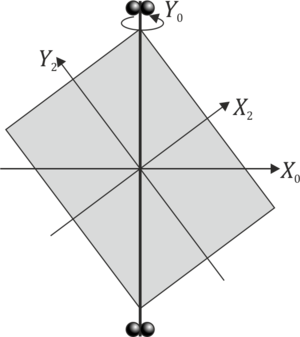
Suponga que esta chapa se monta sobre un eje fijo “1” que pasa por su diagonal y que está articulado mediante rodamientos sin fricción. Los rodamientos se hallan, cada uno de ellos, a una distancia de 60cm del centro de la chapa. Si la chapa se hace girar con velocidad angular constante 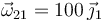 (rad\/s), halle:
(rad\/s), halle:
- El momento cinético respecto al centro de la chapa.
- La energía cinética de la chapa.
- El par aplicado respecto al CM para mantener el sistema en movimiento.
- La fuerza que la placa ejerce sobre los rodamientos en su rotación, suponiendo que estas fuerzas son puramente ortogonales al eje.
Puede despreciarse el efecto del peso. Puede emplearse un sistema intermedio “0” que gira con la misma velocidad angular pero que tiene su eje OY0 coincidente con el OY1
15 Dos discos en varilla giratoria
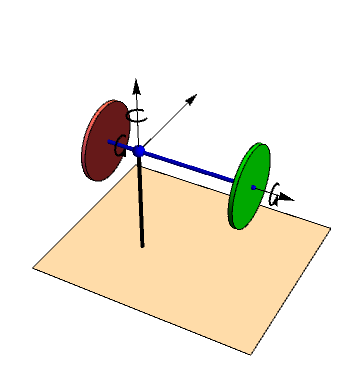
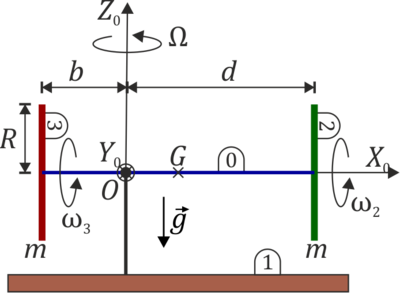
Se tiene un sistema formado por dos discos idénticos, de masa m y radio R (sólidos “2” y “3”). Los discos está montados sobre un eje común (sólido “0”), que es una varilla ideal de masa despreciable. La unión de los discos a la varilla es mediante rodamientos que permiten un giro libre alrededor del eje. La varilla, a su vez está articulada en una rótula a un eje vertical. El punto de articulación, O, no es el centro de la varilla, G, sino que está a una distancia d del disco 2 y a una distancia b del disco 3.
El sistema está sometido a la acción del peso y la posible fuerza de reacción en O.
Tomamos un sistema de ejes rotatorio OX0Y0Z0 en el que el eje OZ0 es el vertical y el OX0 el que pasa por O y los centros de los dos discos. Todas las cantidades deben referirse a la base 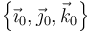 .
Supongamos que los discos giran respecto a su eje común, OX0, con velocidades angulares constantes
.
Supongamos que los discos giran respecto a su eje común, OX0, con velocidades angulares constantes 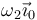 y
y 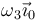 , respectivamente, mientras la varilla gira respecto al eje vertical OZ_0 con velocidad angular constante
, respectivamente, mientras la varilla gira respecto al eje vertical OZ_0 con velocidad angular constante 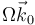 . Para un instante dado:
. Para un instante dado:
- Determine las velocidades angulares de los dos discos respecto a un sistema fijo “1”,
 y
y 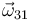 .
.
- Para cada disco determine su tensor de inercia respecto al sistema OX0Y0Z0.
- Calcule la cantidad de movimiento del sistema.
- Halle el momento cinético respecto al punto O de cada disco y el total, suma de los dos,
- Halle la energía cinética de cada disco y la total, suma de las dos.
- Determine la relación que debe haber entre ω2, ω3 y Ω en función de las masas, de g y de las dimensiones del sistema para que el sistema se mantenga girando uniformemente sin que sea preciso aplicar ningún par en O, de forma que el único momento sea el debido al peso.
- Halle la fuerza de reacción en O.
16 Masa suspendida de un polipasto
Un bloque “2” de masa m pende de un polipasto formado por dos poleas. La polea “3” tiene radio r y está unida rígidamente al bloque por una barra de longitud b. La polea “4” tiene el mismo radio y está fijada al techo “1” por otra barra de longitud b. Un hilo inextensible sin masa está atado al techo, pasa por la polea 3, luego por la 4 y está unida al bloque mediante un resorte de constante k y longitud natural 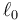 . La longitud del hilo es tal que en ausencia de peso del bloque, el muelle estaría en su longitud natural y el hilo estirado pero sin tensión.
. La longitud del hilo es tal que en ausencia de peso del bloque, el muelle estaría en su longitud natural y el hilo estirado pero sin tensión.
Se cuelga verticalmente el sistema.
- Suponiendo que las poleas no tienen masa, halle la posición de equilibrio del bloque, heq, medida desde el techo. ¿Cuánto vale la tensión del hilo en ese estado?
- Suponiendo que el bloque que se desplaza verticalmente una cantidad A respecto de la posición de equilibrio, determine la frecuencia de las oscilaciones que describe el bloque. ¿Cuánto debe ser el valor máximo de la amplitud si no se quiere que el hilo se destense?
- Suponga ahora que las dos poleas son cilindros macizos de masa m0, con su correspondiente momento de inercia. ¿Cuánto vale en ese caso la frecuencia de las oscilaciones?
- Suponga ahora que el bloque está conectado a un amortiguador de constante γ ¿Cuál es la ecuación de movimiento del bloque en ese caso?

17 Percusión en sistema de dos masas
Supongamos dos masas iguales m / 2 unidas por una barra rígida de longitud b, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento.
- Se comunica una percusión
 perpendicular a la barra a una distancia c de su centro. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?
perpendicular a la barra a una distancia c de su centro. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?
- ¿Cómo cambian los resultados del problema anterior si en lugar de una mancuerna tenemos una barra homogénea de longitud b y masa m a la cual se comunica una percusión
 perpendicular a la barra a una distancia c de su centro?
perpendicular a la barra a una distancia c de su centro?
- ¿Cómo cambian los resultados de los dos problemas anteriores si la barra está articulada a un punto fijo O, situado a una distancia d del centro de la barra? ¿Cuánto valen las fuerzas y momentos de reacción en O?
- ¿Y sí en lugar de estar articulada, está empotrada en O?
18 Péndulo cónico
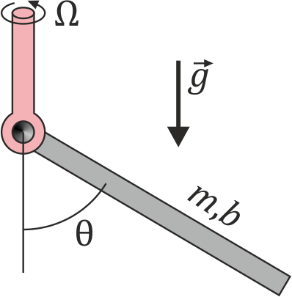
Una barra homogénea de masa m y longitud b se encuentra articulada en su extremo O a un eje vertical que gira con velocidad angular constante 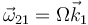 . La barra mantiene en su giro un ángulo constante con la vertical. Determine este ángulo en función de Ω y del resto de constantes del problema. ¿Se levanta la barra para todas las velocidades de giro? ¿Qué velocidad angular se necesita para que la barra quede completamente horizontal?
. La barra mantiene en su giro un ángulo constante con la vertical. Determine este ángulo en función de Ω y del resto de constantes del problema. ¿Se levanta la barra para todas las velocidades de giro? ¿Qué velocidad angular se necesita para que la barra quede completamente horizontal?
19 Anilla ensartada en un aro rodante
Se tiene un sistema formado por un aro “2” de masa m2 que puede rodar sin deslizar sobre una superficie horizontal “1”. Ensartado en este aro se encuentra una pequeña anilla “3” de masa m3 que puede deslizarse sin fricción a lo largo del aro “2”.
Empleando como coordenadas la posición x del centro C del aro “2” a lo largo del eje horizontal y el ángulo θ que la posición de la anilla “3” forma con la vertical, determine:
- Las ecuaciones de movimiento para estas dos coordenadas.
- Dos constantes de movimiento no triviales.
- Suponiendo que el aro y la anilla están en reposo, se sitúa la anilla formando un pequeño ángulo θ0 con la vertical. Determine la frecuencia de las oscilaciones que realiza el sistema.