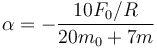Plataforma sobre cilindro rodante (GIE)
De Laplace
Contenido |
1 Enunciado
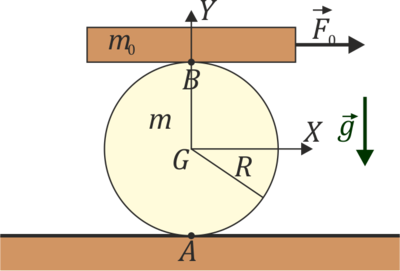
Un rodillo cilíndrico macizo homogéneo de masa m y radio R puede rodar sin deslizar sobre una superficie horizontal. El rodillo se encuentra impulsado por una fina plataforma horizontal de masa m0 cuyo contacto con el rodillo es también de rodadura sin deslizamiento. En un instante dado en que la plataforma está centrada sobre el rodillo y el sistema se halla en reposo se tira de ella con una fuerza 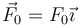 . Determine, en el orden que estime necesario:
. Determine, en el orden que estime necesario:
- La aceleración angular del rodillo, la aceleración del centro del rodillo, y la aceleración de la plataforma.
- Las fuerzas que actúan sobre el rodillo en el punto A, de contacto con el suelo y el punto B, donde se apoya la plataforma.
- Si el coeficiente de rozamiento estático entre el rodillo y el suelo, y entre el rodillo y la plataforma, vale μ, ¿cuál es valor máximo de F0 para que el rodillo no deslice? ¿Por dónde empezará a deslizar, por el punto A o por el punto B?
2 Fuerzas y aceleraciones
A la hora de abordar este problema, hay que tener claro que tenemos dos sólidos en movimiento (aparte del suelo, que está fijo). Por tanto, deben tratarse separadamente, cada uno tendrá su propia aceleración lineal y angular.
Por ello, debemos plantear los diagramas de cuerpo libre por separado.

2.1 Fuerzas y momentos sobre la plataforma
La plataforma o bloque superior está efectuando un movimiento de traslación, por lo que su velocidad angular es nula durante un cierto periodo de tiempo.
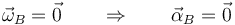
Esto nos permite reducir la dinámica de la plataforma a la de su movimiento de traslación, que además va en la dirección del eje OX. De acuerdo con la 2ª ley de Newton

donde las tres fuerzas que actúan sobre el bloque son
- Su peso,
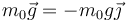 .
.
- La fuerza aplicada externamente
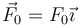 .
.
- La fuerza que el rodillo ejerce sobre la plataforma
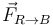 . Esta fuerza es debida al contacto y se compone de dos partes:
. Esta fuerza es debida al contacto y se compone de dos partes:
- Una reacción normal, vertical, que compensa al peso de la plataforma.
- Una fuerza tangencial, que es de rozamiento seco, debida al arrastre de la plataforma sobre el rodillo. Podemos visualizarla mejor imaginando el suelo, el rodillo y la plataforma con dientes de engranajes, con lo que es claro que al tirar de la plataforma, esta ejerce una fuerza sobre el rodillo en el punto de contacto. Por la tercera ley de Newton, el rodillo ejerce una opuesta sobre la plataforma. Esta componente irá hacia atrás (en sentido contrario a F0)
Por tanto, tenemos la ecuación de movimiento
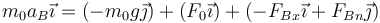
Separando por componentes

La segunda nos permite hallar la fuerza normal en B,

pero la primera no nos proporciona la aceleración, ya que introduce una incógnita adicional, la fuerza de contacto en B. Para determinarla debemos ir a la ecuación para la dinámica del rodillo.
2.2 Fuerzas y momentos sobre el rodillo
Operando de la misma manera tenemos, para la aceleración del centro del rodillo (centro de masas de éste):
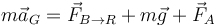
La fuerza del bloque sobre el rodillo será la opuesta a la de la sección anterior. La fuerza en A es del mismo tipo y se debe al contacto del suelo con el rodillo.
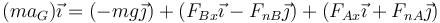
Separando por componentes

Esto nos permite hallar la reacción normal en A
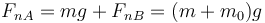
pero no la fuerza en B, ya que de hecho introduce dos incógnitas adicionales, la aceleración del CM y la fuerza tangencial en A.
Es evidente que solo con la 2ª ley de Newtton no se puede resolver el problema.
En el caso del rodillo debemos considerar también la rotación alrededor del CM. Por tratarse de un cuerpo simétrico alrededor del eje de rotación, la ecuación que gobierna ésta es
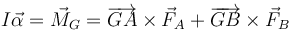
lo que nos da la ecuación

El momento de inercia es de la forma

Esto nos da una nueva ecuación que liga a las fuerzas en A y B, pero introduce una nueva incógnita, la aceleración angular.
Para cerrar el sistema, necesitamos relacionar la aceleración de la plataforma, la del centro del rodillo, y la angular del rodillo. Para relacionarlas debemos recurrir a la cinemática.
2.3 Relaciones entre las aceleraciones
Para relacionar aG y α tenemos que, por ser el contacto en A uno de rodadura sin deslizamiento, la velocidad instantánea en entre punto es nula
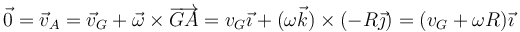
de donde
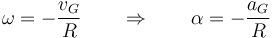
La segunda relación la sacamos de que en todo momento la velocidad en B es el doble de la de G
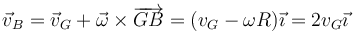
y por tanto
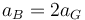
Para precisar, esta aceleración es la del punto B de la plataforma, que solo avanza, no la del B del rodillo, que también tiene aceleración normal.
2.4 Sistema de ecuaciones
Resumiendo, tenemos el siguiente sistema de ecuaciones

Esto es un sistema de ecuaciones lineales que se resuelve de forma sencilla. De la 2ª, la 3ª y la 4ª

Llevando esto a la 1ª y 5ª obtenemos la aceleración del centro del rodillo
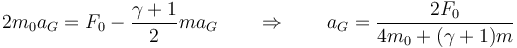
y de la plataforma

así como la aceleración angular
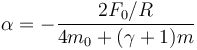
la fuerza de contacto en B
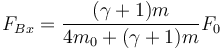
y en A
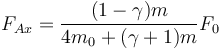
Dado que  (1/2 para el cilindro macizo, 1 para el hueco, 2/3 para la esfera hueca, 2/5 para la maciza), esta fuerza es siempre menor en módulo que la de B y además, en contra de lo que podría pensarse va hacia adelante, no hacia atrás.
(1/2 para el cilindro macizo, 1 para el hueco, 2/3 para la esfera hueca, 2/5 para la maciza), esta fuerza es siempre menor en módulo que la de B y además, en contra de lo que podría pensarse va hacia adelante, no hacia atrás.
3 Fuerza máxima
La condición para que no se produzca deslizamiento es que la fuerza tangencial no supere a μ por la normal.

Dado que | FAx | < | FBx | y que | FnA | > | FnB | el deslizamiento en B se producirá siempre antes que en A. Por tanto, la condición buscada es
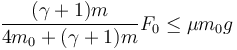
lo que nos da la fuerza máxima
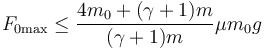
Podemos ver que en el caso de un rodillo infinitamente pesado (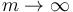 ) se reduce a la fórmula del deslizamiento habitual (
) se reduce a la fórmula del deslizamiento habitual (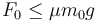 )
)
4 Casos particulares de diferentes cuerpos rodantes
4.1 Cilindro macizo
Haciendo γ = 1 / 2

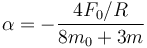


4.2 Cilindro hueco
Haciendo γ = 1

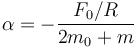

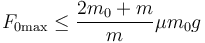
4.3 Esfera hueca
Haciendo γ = 2 / 3

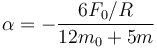

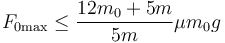
4.4 Esfera maciza
Haciendo γ = 2 / 5