Péndulo Compuesto (I) (CMR)

De Laplace

Contenido

1 Enunciado
2 Ecuación de movimiento
- 2.1 A partir de la energía
- 2.2 A partir de fuerzas y momentos
3 Oscilaciones pequeñas
4 Paso por la vertical
5 Posición general

1 Enunciado

Se tiene un péndulo compuesto consistente en una barra homogénea de longitud $2 b$ y masa $m$ suspendida por un punto situado O a una distancia $d$ del centro G de la barra ( $d < b$ ).:

Determine el periodo de oscilación de la barra si se suelta desde un ángulo pequeño $θ 0$ respecto a la vertical.
Suponga ahora que la barra se sitúa en el equilibrio inestable con el CM por encima del punto de apoyo y desde ahí se suelta con una velocidad inicial muy pequeña. Para el instante en que pasa por la vertical, calcule:
1. La velocidad angular de la barra y la velocidad lineal de los extremos de la barra.
2. Calcule la fuerza ejercida sobre el punto de anclaje.
3. Calcule la tensión en cada punto de la barra.
Repita los cálculos del apartado anterior para el momento en que forma un ángulo $θ$ con la vertical.

2 Ecuación de movimiento

2.1 A partir de la energía

Al ser un sistema con un solo grado de libertad (el ángulo que forma con la vertical), podemos determinar la ecuación de movimiento a partir de la energía mecánica, que e suna cantidad constante al ser un sistema conservativo

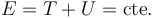
$E=T+U=\mathrm{cte.}\,$

La energía cinética es la correspondiente a una rotación respectoa un punto fijo O

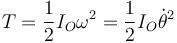
$T=\frac{1}{2}I_O \omega^2=\frac{1}{2}I_O \dot{\theta}^2$

siendo el momento de inercia, de acuerdo con el teorema de Steiner

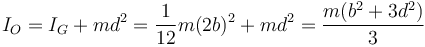
$I_O=I_G+md^2= \frac{1}{12}m(2b)^2+md^2 = \frac{m(b^2+3d^2)}{3}$

La energía potencial, tomando como referencia el punto O, es la correspondiente al peso. La posición vertical del CM es $z G = - d cos(θ)$ , por lo que

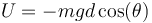
$U=-mgd\cos(\theta)\,$

Esto da la energía mecánica

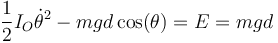
$\frac{1}{2}I_O\dot{\theta}^2 - mgd \cos(\theta)=E=mgd$

El valor de la constante sale de que la posición inicial es vertical y hacia arriba ( $θ = π$ ) en reposo.

Como esta cantidad es constante, su derivada respecto al tiempo se anula

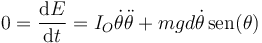
$0=\frac{\mathrm{d}E}{\mathrm{d}t}=I_O\dot{\theta}\ddot{\theta}+mgd\dot{\theta}\,\mathrm{sen}(\theta)$

Sacando factor común

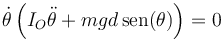
$\dot{\theta}\left(I_O\ddot{\theta}+mgd\,\mathrm{sen}(\theta)\right)=0$

lo que nos da la ecuación de movimiento

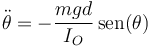
$\ddot{\theta}=-\frac{mgd}{I_O}\,\mathrm{sen}(\theta)$

2.2 A partir de fuerzas y momentos

Un método más sistemático, que no depende de si el sistema es conservativo o no, o de si tiene uno o más grados de libertad, consiste en usar las ecuaciones de Newton y Euler para la traslación y la rotación.

De acuerdo con la segunda ley de Newton

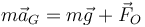
$m\vec{a}_G=m\vec{g}+\vec{F}_O$

siendo 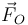$\vec{F}_O$ la fuerza de reacción en el soporte. Esta fuerza es desconocida de antemano, por lo que esta ecuación no es suficiente para determinar la ecuación de movimiento. De hecho, la emplearemos más tarde para calcular esta fuerza de reacción.

La ecuación de Euler para la rotación es

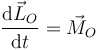
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O$

siendo el momento aplicado

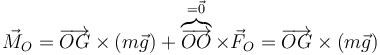
$\vec{M}_O=\overrightarrow{OG}\times(m\vec{g})+\overbrace{\overrightarrow{OO}}^{=\vec{0}}\times\vec{F}_O=\overrightarrow{OG}\times(m\vec{g})$

Vemos que al reducir el problema en el punto O eliminamos el momento debido a la fuerza de reacción.

El único momento es el del peso, que es igual a

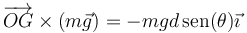
$\overrightarrow{OG}\times(m\vec{g})=-mgd\,\mathrm{sen}(\theta)\vec{\imath}$

Aquí hemos tomado un sistema de ejes en el que el OZ es vertical, el péndulo oscila en el plano OYZ y por tanto el eje OX es el normal al plano hacia afuera. Para un ángulo $θ > 0$ el par produce un giro en torno a OX pero en sentido horario (negativo). Su módulo es igual al módulo del primero (d) por el módulo del segundo (mg) por el seno del ángulo que forman.

El momento cinético $\vec{L}_O$ lo calculamos observando que se trata de una rotación respecto a un eje fijo (OX), que además es un eje principal

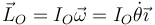
$\vec{L}_O=I_O\vec{\omega}=I_O\dot{\theta}\vec{\imath}$

Derivamos aquí respecto al tiempo

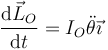
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=I_O\ddot{\theta}\vec{\imath}$

e igualamos al momento de las fuerzas, resultando de nuevo

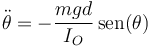
$\ddot{\theta}=-\frac{mgd}{I_O}\,\mathrm{sen}(\theta)$

Una vez que tenemos esta ecuación, podemos determinar, si lo deseamos, la fuerza en el soporte como

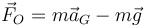
$\vec{F}_O=m\vec{a}_G-m\vec{g}$

3 Oscilaciones pequeñas

Si la barra se suelta desde una posición próxima a la vertical, el ángulo θ será pequeño y puede hacerse la aproximación

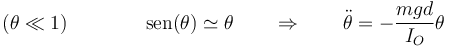
$(\theta\ll 1)\qquad\qquad\mathrm{sen}(\theta)\simeq \theta\qquad\Rightarrow\qquad \ddot{\theta}=-\frac{mgd}{I_O}\theta$

Esta última es la ecuación de un oscilador armónico de frecuencia propia

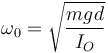
$\omega_0=\sqrt{\frac{mgd}{I_O}}$

y por tanto el periodo de las pequeñas oscilaciones del péndulo vale

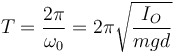
$T=\frac{2\pi}{\omega_0}=2\pi\sqrt{\frac{I_O}{mgd}}$

Si sustituimos el momento de inercia para la barra

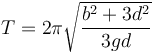
$T=2\pi\sqrt{\frac{b^2+3d^2}{3gd}}$

El resultado es independiente de la masa. Se hace infinito para 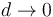$d\to 0$ lo cual quiere decir que si colgamos la barra por su punto central, no gira, independientemente de si está inclinada o no.

4 Paso por la vertical

4.1 Velocidad angular

En el caso de que se suelte desde la vertical, con el CM encima del punto de apoyo (lo que es la posición inestable de un péndulo invertido) no vale la aproximación de ángulos pequeños, pero sí sigue siendo cierta la conservación de la energía mecánica

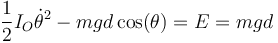
$\frac{1}{2}I_O\dot{\theta}^2 - mgd \cos(\theta)=E=mgd$

Cuando pasa por la vertical $θ = 0$ , lo que nos da

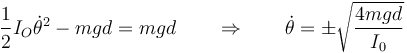
$\frac{1}{2}I_O\dot{\theta}^2 - mgd =mgd\qquad\Rightarrow\qquad \dot{\theta}=\pm\sqrt{\frac{4mgd}{I_0}}$

El doble signo corresponde a las dos posibilidades de caída. El signo positivo sería la caída hacia la izquierda y el negativo hacia la derecha.

En forma vectorial

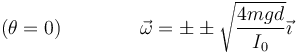
$(\theta=0)\qquad\qquad \vec{\omega}=\pm \pm\sqrt{\frac{4mgd}{I_0}}\vec{\imath}$

En el momento en que pasa por la vertical inferior la velocidad angular es máxima, por lo que la aceleración angular, su derivada, es nula.

$(\theta=0)\qquad\qquad\vec{\alpha}=\vec{0}$

4.2 Fuerza en el soporte

La fuerza de que ejerce el soporte sobre la barra lo hallamos a partir de la segunda ley de Newton

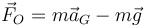
$\vec{F}_O=m\vec{a}_G-m\vec{g}$

La aceleración del centro de masas es la correspondiente a un punto de un sólido en rotación alrededor de O

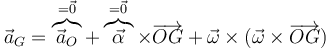
$\vec{a}_G=\overbrace{\vec{a}_O}^{=\vec{0}}+\overbrace{\vec{\alpha}}^{=\vec{0}}\times\overrightarrow{OG}+\vec{\omega}\times(\vec{\omega}\times\overrightarrow{OG})$

Justo en el momento en que pasa por la vertical

$\overrightarrow{OG}=-d\vec{\jmath}\qquad\qquad\vec{\omega}=\dot{\theta}\vec{\imath}$

lo que nos da

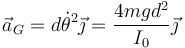
$\vec{a}_G=d\dot{\theta}^2\vec{\jmath}=\frac{4mgd^2}{I_0}\vec{\jmath}$

y la fuerza de reacción

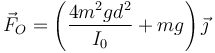
$\vec{F}_O=\left(\frac{4m^2gd^2}{I_0}+mg\right)\vec{\jmath}$

Vemos que es superior al peso, ya que también se produce la aceleración del CM. Si sustituimos el valor del momento de inercia

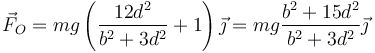
$\vec{F}_O=mg\left(\frac{12d^2}{b^2+3d^2}+1\right)\vec{\jmath}=mg\frac{b^2+15d^2}{b^2+3d^2}\vec{\jmath}$

En el caso de que la barra esté colgada por su extremo

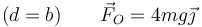
$(d=b)\qquad\vec{F}_O=4mg\vec{\jmath}$

4.3 Tensión

La tensión en un hilo ideal sin masa tiene el mismo módulo en todos sus puntos. En una barra con masa, en cambio, la tensión cambia d eun punto a otro, ya que hay que tener en cuenta la inercia de la propia barra.

Consideramos en primer lugar el segmento de barra que queda por debajo del punto de apoyo. Sea r la posición a lo largo de este tramo. La masa de un elemento de logitud $d r$ es

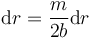
$\mathrm{d}r=\frac{m}{2b}\mathrm{d}r$

Sobre este elemento actúan tres fuerzas: la tensión desde arriba, la tensión por abajo y el peso. De acuerdo con la segunda ley de Newton

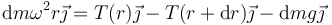
$\mathrm{d}m\omega^2 r\vec{\jmath}=T(r)\vec{\jmath}-T(r+\mathrm{d}r)\vec{\jmath}-\mathrm{d}mg\vec{\jmath}$

De aquí llegamos a la ecuación

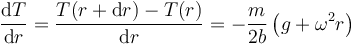
$\frac{\mathrm{d}T}{\mathrm{d}r}=\frac{T(r+\mathrm{d}r)-T(r)}{\mathrm{d}r}=-\frac{m}{2b}\left(g+\omega^2 r\right)$

que integrada da

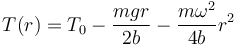
$T(r)=T_0-\frac{mgr}{2b}-\frac{m\omega^2}{4b}r^2$

La cnstante de integración la obtenemos de que en el extremo de la barra la tensión es nula

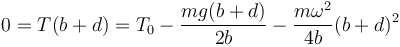
$0=T(b+d)=T_0-\frac{mg(b+d)}{2b}-\frac{m\omega^2}{4b}(b+d)^2$

lo que nos da finalmente

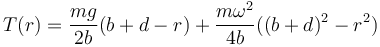
$T(r) =\frac{mg}{2b}(b+d-r)+\frac{m\omega^2}{4b}((b+d)^2-r^2)$

Si sustituimos el vale de $ω 2$ para este caso particular

5 Posición general

5.1 Velocidad angular

5.2 Fuerza en el soporte

5.3 Tensión

Péndulo Compuesto (I) (CMR)

De Laplace

Contenido

1 Enunciado

2 Ecuación de movimiento

2.1 A partir de la energía

2.2 A partir de fuerzas y momentos

3 Oscilaciones pequeñas

4 Paso por la vertical

4.1 Velocidad angular

4.2 Fuerza en el soporte

4.3 Tensión

5 Posición general

5.1 Velocidad angular

5.2 Fuerza en el soporte

5.3 Tensión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES