Anilla ensartada en un aro rodante
De Laplace
Contenido |
1 Enunciado
Se tiene un sistema formado por un aro “2” de masa m2 que puede rodar sin deslizar sobre una superficie horizontal “1”. Ensartado en este aro se encuentra una pequeña anilla “3” de masa m3 que puede deslizarse sin fricción a lo largo del aro “2”.
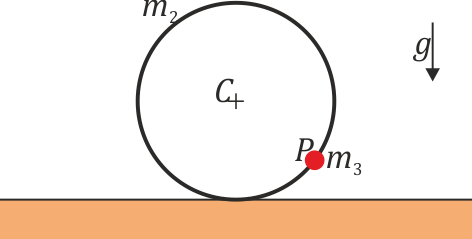
Empleando como coordenadas la posición x del centro C del aro “2” a lo largo del eje horizontal y el ángulo θ que la posición de la anilla “3” forma con la vertical, determine:
- Las ecuaciones de movimiento para estas dos coordenadas.
- Dos constantes de movimiento no triviales.
- Suponiendo que el aro y la anilla están en reposo, se sitúa la anilla formando un pequeño ángulo θ0 con la vertical. Determine la frecuencia de las oscilaciones que realiza el sistema.
2 Ecuaciones de movimiento
Cada uno de los dos cuerpos “2” y “3” obedece las ecuaciones dadas por el teorema de la cantidad de movimiento y el teorema del momento cinético. En cada caso debemos incluir las posibles fuerzas de reacción sobre cada uno de los cuerpos.
2.1 Para el aro
2.1.1 Teorema de la cantidad de movimiento
El aro experimenta las siguientes fuerzas externas:
- Su peso
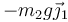
- La reacción del suelo en el punto de contacto A, la cual tiene dos componentes
- Una vertical
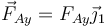 que impide que el aro atraviese el suelo, y mantiene el centro a una altura constante R.
que impide que el aro atraviese el suelo, y mantiene el centro a una altura constante R.
- Una horizontal,
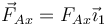 que impide que el aro deslice, de manera que solo ruede.
que impide que el aro deslice, de manera que solo ruede.
- Una vertical
- Una fuerza de reacción debida a la anilla. El vínculo de que la anilla permanezca en el aro se consigue realizando una fuerza normal sobre ésta
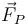 y, por la tercera ley de Newton, una fuerza igual y de sentido contrario
y, por la tercera ley de Newton, una fuerza igual y de sentido contrario 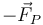 se aplica en el aro.
se aplica en el aro.
Esto nos da la sigueinte relación
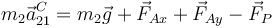
La aceleración del centro del aro es puramente horizontal
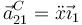
Para expresar la fuerza 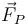 usamos un sistema “3” de ejes que está girado un ángulo θ respecto al sistema “1”, de manera que
usamos un sistema “3” de ejes que está girado un ángulo θ respecto al sistema “1”, de manera que 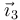 es tangente al aro y
es tangente al aro y 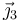 es radial y hacia adentro.
es radial y hacia adentro.

( ). Estos vectores se relacionan directamente con los correspondientes a las coordenadas polares.
). Estos vectores se relacionan directamente con los correspondientes a las coordenadas polares.
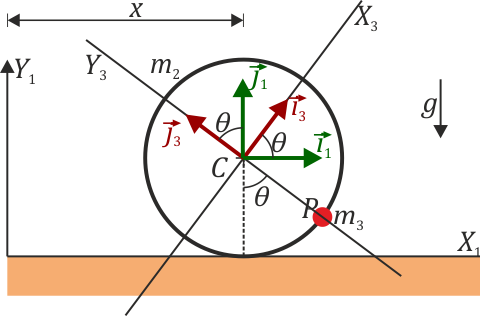
Tenemos entonces
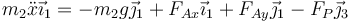
Separando por componentes
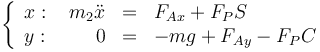
Estas dos ecuaciones no son suficientes para determinar el movimiento del aro.
2.1.2 Teorema del momento cinético
La tercera ecuación para el aro la da la evolución del momento cinético. Respecto al centro del aro
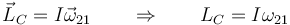
Podemos usar escalares ya que ambos vectores apuntan en la dirección del eje Z, perpendicular al plano de movimiento. Podemos relacionar la velocidad angular con la velocidad de avance del centro por la condición de rodadura

y de aquí
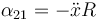
La única fuerza que provoca un momento respecto al centro es la tangencial en el punto de contacto. Por ello
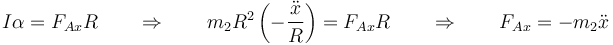
Llevando esto a la componente horizontal del TCM podemos eliminar esta fuerza de reacción y queda

Para completar el sistema necesitamos además las ecuaciones para la anilla.
2.2 Para la anilla
Considerando la anilla como una partícula, no es necesario considerar la rotación. En ese caso nos basta con el TCM, es decir, con la 2ª ley de Newton.
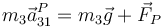
La aceleración de la partícula se relaciona con la del centro del aro como
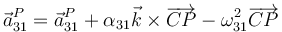
siendo

(aquí estamos imaginando un sólido o sistema de referencia "3" cuyo eje OY3 sería el radio por C y P).
Además

Esto nos da
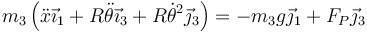
Esta expresión combina dos bases vectoriales. para obtener una ecuación escalar debemos proyectar sobre una dirección dada.
2.3 Ecuaciones de movimiento
Si proyectamos la ecuación vectorial de la anilla hacemos sobre 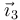 eliminamos la fuerza de reacción FP y queda
eliminamos la fuerza de reacción FP y queda

Si proyectamos sobre la dirección horizontal 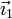

Sumamos esta ecuación con la correspondiente al aro

y nos queda
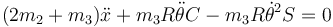
Tenemos entonces el sistema

De aquí podemos despejar las segundas derivadas
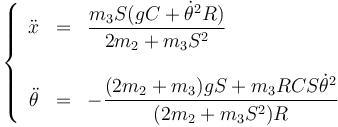
La segunda de las ecuaciones contiene solo a la variable θ y sus derivadas, con lo que puede ser resuelta sin tener en cuenta la posición x del anillo, que puede determinarse posteriormente.
Como límite de interés podemos ver qué pasa si 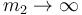 , es decir, el aro es infinitamente masivo. En ese caso
, es decir, el aro es infinitamente masivo. En ese caso
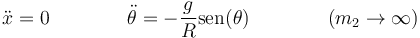
es decir, el aro no se mueve, mientras que la anilla cumple la ecuación del péndulo.
3 Constantes de movimiento
3.1 Cantidad de movimiento generalizada
En este sistema no se conserva la cantidad de movimiento,
- En su componente vertical, porque está el peso, que acelera a la anilla en esta dirección.
- En la componente horizontal, porque hay una fuerza externa FAx que acelera el CM del sistema.
No obstante, si examinamos la ecuación de movimiento
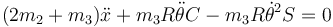
vemos que esta ecuación equivale a
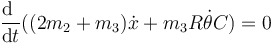
y por tanto, una constante no trivial es
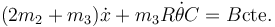
Esta magnitud generaliza la cantidad de movimiento, incorporando un término de rotación.
De hecho, puede integrarse una segunda vez y dar
con lo cual, si quisiéramos, podríamos obtener una segunda constante no trivial como
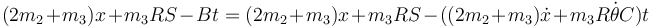
No obstante, hay una segunda constante con mayor significado físico.
3.2 Energía mecánica
En este sistema se conserva la energía mecánica. La justificación para ello es que:
- El peso es una fuerza conservativa que deriva de una energía potencial.
- La fuerza de reacción
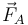 se aplica sobre un punto de velocidad nula (el de contacto con el suelo) y por tanto no desarrolla potencia.
se aplica sobre un punto de velocidad nula (el de contacto con el suelo) y por tanto no desarrolla potencia.
- La fuerza interna
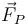 podría, en principio, afectar a la energía, sin embargo, su potencia es suma de la que hace sobre cada sólido
podría, en principio, afectar a la energía, sin embargo, su potencia es suma de la que hace sobre cada sólido
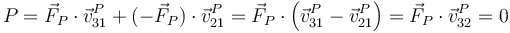
- ya que esta fuerza es radial y la velocidad de la anilla respecto al aro es tangencial.
Por tanto la energía mecánica se conserva. Ésta es suma de
- La energía cinética del aro, suma de la de traslación y la de rotación.
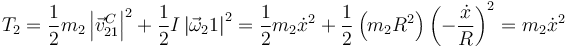
- La energía cinética de la partícula
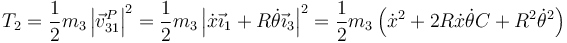
- La energía potencial de la partícula, que podemos medir desde la altura del centro del aro
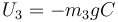
Sumando estas tres cantidades resulta la energía

Podemos comprobar que esta cantidad es una constante derivando respecto al tiempo y sustituyendo las ecuaciones de movimiento.
4 Pequeñas oscilaciones
La ecuación de movimiento para el ángulo θ es
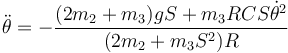
Si consideramos pequeñas oscilaciones alrededor del punto más bajo podemos hacer las aproximaciones
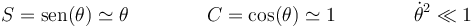
con esto queda la ecuación aproximada
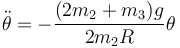
que es la de un oscilador armónico con frecuencia

Para 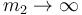 se recupera de nuevo la ecuación del péndulo simple.
se recupera de nuevo la ecuación del péndulo simple.





