Problemas de dinámica de un sistema de partículas F1-GIC
De Laplace
1 Problemas del boletín
1.1 Centro de masas de sistemas continuos
Calcula por la posición del centro de masas de estos sistemas
- Una barra homogénea delgada de longitud h y masa M.
- Una barra de longitud a y densidad lineal de masa λ = Cx, siendo x la distancia a un extremo de la barra y C una constante.
- Una barra homogénea delgada en forma de semicírculo de radio a y masa M.
- Dos esferas macizas de masas M1 y M2 y radios R y 2R, unidas por un cilindro de masa M3 y longitud L.
- Una esfera maciza de radio 2b, densidad homogénea ρ0, con una cavidad también esférica, de radio b, cuyo centro se encuentra a una distancia b del centro de la esfera original.
1.2 Bloque deslizando sobre una cuña apoyada en una balanza
Un bloque de masa m1 se desliza sin rozamiento sobre una cuña de masa m2 que forma un ángulo β con la horizontal. El conjunto está sobre una balanza de muelle. El plato de la balanza permanece en reposo durante toda la experiencia.
- Determina la aceleración de la masa m1 al desplazarse sobre la cuña.
- Calcula la aceleración del cento de masas del sistema cuña-masa.
- ¿Cuál es la lectura en la balanza mientras cae la masa?
1.3 Momento cinético de una barra
Una barra homogénea de masa m y longitud L gira en torno a un eje perpendicular a ella y que pasa
por su centro, con velocidad angular uniforme  .
.
- Calcula el momento angular de la barra respecto a su punto central.
- Ahora el eje de giro pasa por uno de sus extremos. Calcula el momento angular de la barra en este caso, respecto a un punto del eje de giro.
- En la situación anterior, la longitud de la barra se multiplica por dos, mientras que su masa permanece constante. ¿Cómo cambia la velocidad angular? ¿Y si se divide por dos?
1.4 Polea pesada con dos masas
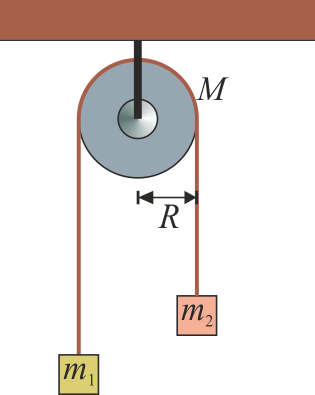
Una máquina de Atwood consiste en una polea de masa M y radio R de la que cuelgan dos masas m1 y m2, una a cada lado. El sistema está sometido a la acción de la gravedad.
- Suponiendo que las dos masas parten del reposo, determina sus aceleraciones, la velocidad angular con que rota la polea y la tensión de la cuerda a cada lado de la polea.
- Resuelve el mismo problema suponiendo que hay un momento de rozamiento sobre la polea constante e igual a Mr.
- Obtén los valores numéricos de las soluciones para los datos
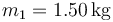 ,
, 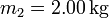 ,
, 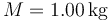 ,
, 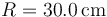
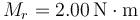 .
.
1.5 Volante de inercia
Un volante de inercia es un gran cilindro en rotación que puede usarse para almacenar energía. Estima la energía cinética que puede almacenar un volante de inercia de masa 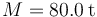 y radio
y radio 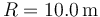 . Supón que el volante puede girar sin romperse a una velocidad angular de 100 rpm. ¿Cuánto tiempo podría funcionar un horno microondas de
. Supón que el volante puede girar sin romperse a una velocidad angular de 100 rpm. ¿Cuánto tiempo podría funcionar un horno microondas de 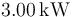 de potencia con la energía almacenada en el volante?
de potencia con la energía almacenada en el volante?
1.6 Colisiones de dos partículas
Una partícula de masa M se encuentra en reposo. Otra partícula de masa m impacta con ella con una velocidad v. Después del choque las dos partículas se mueven en la misma dirección en la que se movía la partÍcula m.
- Encuentra la expresión de la velocidad de cada una de las partículas en función de sus masas y de v si el choque es perfectamente elástico.
- Calcula la velocidad si el choque es completamente inelástico. ¿Cuánta energía cinética se pierde en el choque?
- ¿Qué ocurre si
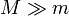 ? ¿Y si
? ¿Y si 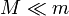 ?
?
1.7 Mono intentado alcanzar unos plátanos
Un mono de masa m cuelga de una cuerda ideal inextensible y sin masa, que está enrollada en una polea de radio R. En el otro extremo de la cuerda hay un racimo de plátanos que tienen la misma masa m del mono. Los plátanos están por encima del mono, como se indica en la figura. Éste los ve y comienza a trepar por la cuerda para intentar alcanzarlos.
- Supongamos que la masa de la polea es despreciable. ¿Consigue el mono atrapar los platanos antes de que estos alcancen la altura de la polea?
- Supongamos ahora que la polea es un aro con masa M. En el instante inicial los plátanos están a una distancia L de la altura de la polea y el mono a una distancia 2L. El mono sube la cuerda con velocidad v0 respecto a la polea. ¿Que condición debe cumplir M para que el mono pueda alcanzar los plátanos antes de que estos lleguen a la polea?
1.8 Partículas en colisión inelástica unidireccional
Una partícula de masa m y velocidad  colisiona con otra partícula de masa m que está en reposo. Después del choque las dos partículas se mueven en la dirección de
colisiona con otra partícula de masa m que está en reposo. Después del choque las dos partículas se mueven en la dirección de  . El coeficiente de restitución del choque es CR.
. El coeficiente de restitución del choque es CR.
- Determina la velocidad de las dos partículas después del choque.
- Calcula la pérdida de energía cinética en función del valor del coeficiente de restitución. ¿Cómo es la variación de energía cinética en los valores límites del coeficiente de restitución?
2 Otros problemas
2.1 Cuatro partículas en un cuadrado
Se tienen 4 masas que ocupan los vértices de un cuadrado de lado 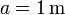 . Calcula la
posición del centro de masas del sistema en cada uno de los casos siguientes
. Calcula la
posición del centro de masas del sistema en cada uno de los casos siguientes
 .
.
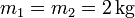 ,
, 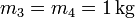 .
.
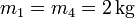 ,
, 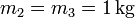 .
.
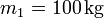 ,
,  .
.

2.2 Ejemplo de un sistema de partículas
Tres partículas puntuales se encuentran en un cierto instante en los vértices de un triángulo. Las masas, posiciones y velocidades de las partículas son, en el SI,
| i | mi | 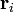
| 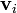
|
|---|---|---|---|
| 1 | 5 | 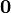
| 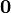
|
| 2 | 4 | 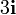
| 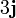
|
| 3 | 3 | 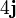
| 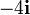
|
Las tres partículas están conectadas por resortes con la misma constante k = 30N / m y longitud natural nula. No hay más fuerzas actuando en el sistema. Para el instante indicado:
- Determina la aceleración de cada partícula.
- Calcula la posición, velocidad y aceleración del CM.
- Calcula el momento cinético del sistema respecto al origen y respecto al CM.
- Halla la energía cinética del sistema respecto al origen y respecto al CM.
- Calcula las derivadas respecto al tiempo de la cantidad de movimiento, del momento cinético y de la energía cinética.
2.3 Dos partículas unidas por un oscilador armónico
Supongamos dos partículas de la misma masa m unidas por un resorte de constante k y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; y se le comunica a la partícula 2 una velocidad v0 alejándola de la primera, mientras que la partícula 1 se encuentra inicialmente en reposo. ¿Cuál es el movimiento subsiguiente de ambas partículas?
2.4 Dos partículas unidas por una barra
Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial v0 perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?
2.5 Barra oscilando respecto a uno de sus extremos
Una barra homogénea de longitud L y masa M cuelga por uno de sus extremos de modo que se encuentra en equilibio en posición vertical. Analiza el movimiento de la barra si se separa de la vertical un ángulo θ0 pequeño.
2.6 Barra girando
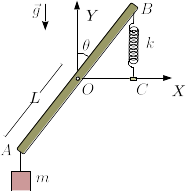
La barra de la figura puede girar sobre su extremo inferior O. La barra es homogénea, de lonigtud L y masa M. En el instante inicial se encuentra en posición vertical (θ(0) = π / 2). En ese instante empieza a moverse de modo que el extremo A tiene una velocidad instantánea 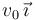 .
.
- Calcula la velocidad angular de la barra en el instante inicial.
- Si I es el momento de inercia de la barra respecto a un eje perpendicular al plano OXY y que pasa por el punto O, encuentra la ecuación diferencial que describe el movimiento de la barra.
- Encuentra la expresión que da la velocidad angular con la que gira la barra en función del ángulo θ.
2.7 Polea con masa colgando y freno
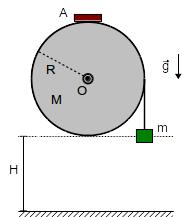
El disco de la figura, de radio R y masa M, puede rotar sin rozamiento alrededor de un eje perpendicular al plano del papel y que pasa por O. La masa m cuelga de una cuerda vertical, inextensible y sin masa, de modo que su altura respecto del suelo H coincide con la del borde inferior del disco. En el punto A, un freno ejerce una fuerza de rozamiento sobre el disco de módulo FR. Todo el sistema está sometido a la fuerza de la gravedad con la dirección que se indica en la figura. El momento de inercia de un disco respecto a un eje perpendicular a él que pasa por su centro es I = MR2 / 2.
- Dibuja el diagrama de cuerpo libre del disco y de la masa, cuando el sistema está en equilibrio estático.
- ¿Cuánto valen los módulos de todas las fuerzas que actúan sobre el disco en situación de equilibrio estático?
- Liberamos el freno y la masa m cae con velocidad siempre vertical. Calcula la aceleración angular del disco.
- Calcula el módulo de la velocidad de la masa cuando impacta en el suelo y la velocidad angular de rotación del disco en ese instante.
2.8 Cilindro desenrollándose en cuerda vertical
Un disco homogéneo de masa m y radio R se desenrolla bajo la acción de la gravedad sobre una cuerda vertical, como se indica en la figura, de forma que la velocidad del punto de contacto del disco con la cuerda es siempre nula. La cuerda se mantiene siempre vertical. El punto O al que está atada la cuerda es un punto fijo.
- Escribe el vector de posición, velocidad y aceleración del centro del disco. ¿Cuál es la relación entre la velocidad del centro del disco y su velocidad de rotación?
- En el instante inicial el disco está en reposo con x(0) = 0. Calcula la velocidad del centro del disco en función de su posición.
- Calcula la fuerza neta que actúa sobre el disco y la tensión de la cuerda.
2.9 Masa con cuerda desenrollándose de un disco
Una masa m desliza sobre una superficie horizontal lisa. Está conectada a un muelle de constante elástica k = mg / R y longitud natural l0 = R. Por el otro lado tira de ella una cuerda sin masa que puede enrollarse y desenrollarse en un disco de masa m y radio R. El disco puede rotar alrededor de un eje perpendicular a él que pasa por su centro. El sistema está sometido a la acción de la gravedad. En el instante inicial la masa se encuentra en el punto B. Tanto la masa como el disco están en reposo en ese instante inicial. Durante todo el movimiento la cuerda permanece tensa. El momento de inercia de un disco de masa M y radio R respecto a un eje perpendicular a él que pasa por su centro es I = MR2 / 2.
- Calcula la rapidez de la masa cuando llega al punto O
- ¿Qué trabajo ha hecho la cuerda sobre la masa durante su movimiento?
- Si el contacto entre la masa y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico μ, calcula la velocidad de la masa en el punto O
- ¿Qué condición debe cumplir μ para que la masa no llegue al punto O?
2.10 Disco con muelle enganchado en su centro
Un disco de masa m y radio R rueda sin deslizar sobre una superficie horizontal rugosa. El centro
del disco está conectado al punto A con un muelle de constante elástica k = mg / R y longitud natural nula.
Además, actúa sobre el disco un par de fuerzas 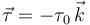 , con τ0 > 0. En el instante
inicial el disco estaba en reposo y su centro se encontraba sobre el eje Y.
, con τ0 > 0. En el instante
inicial el disco estaba en reposo y su centro se encontraba sobre el eje Y.
- Dibuja el diagrama de cuerpo libre del disco.
- Calcula la aceleración del centro del disco.
- Si τ0 = mgR, ¿para que valor de x el disco empieza a deslizar?
2.11 Disco con muelle: energía
El disco de la figura rueda sin deslizar sobre una superficie horizontal rugosa. El punto más alto del disco está conectado a un muelle de constante elástica k y longitud natural nula. El otro extremo del muelle está conectado al punto A del eje OY. El disco se suelta desde la posición de la figura con situación inicial de reposo. ¿Cuánto vale la velocidad del centro del disco en el instante en que está sobre el eje Y? El disco puede atravesar el eje vertical.
Nota: El momento de inercia del disco respecto a un eje perpendicular a él que pase por su centro es I = mR2 / 2.
2.12 Barra con muelle vertical y masa colgando
Una barra homogénea, de masa m y longitud 2L, está articulada en el origen de coordenadas en su punto medio, de modo que ese punto permanece fijo. De su extremo izquierda cuelga una masa m, conectada a la barra por un hilo inextensible y sin masa. El hilo se mantiene siempre vertical. El extremo derecho está conectado a un muelle ideal de constante elástica k y longitud natural nula. El otro extremo del muelle se ancla en un pasador C, de modo que el muelle siempre permanece vertical. La gravedad actúa hacia abajo, como se indica en la figura.
- Dibuja el diagrama de fuerzas que actúan sobre la barra.
- Determina las posiciones de equilibrio de la barra, así como la expresión de la fuerza vincular que actúa sobre ella en cada una de las posiciones.
- Supongamos que sustitiumos la masa en el extremo A por una tuerca apretada en O, que ejerce un momento de fuerzas sobre la barra
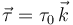 . ¿Cuánto vale θ en este caso en situación de equilibrio?
. ¿Cuánto vale θ en este caso en situación de equilibrio?
- Partiendo de la situación descrita en 3, con la barra en reposo y con θ = π / 4, aflojamos completa y rápidamente la tuerca. ¿Cuánto vale la energía cinética de la barra y la rapidez del punto B cuándo este está sobre el eje OX? (Dato: IO = mL2 / 3)
2.13 Propulsión a reacción
Un cohete a reacción se impulsa en el espacio emitiendo gases a cierta velocidad en el sentido opuesto a su propio movimiento. Sea un cohete que tiene una masa M0 y lleva una carga inicial de combustible m0. Este combustible es expulsado a ritmo constante 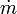 con una velocidad constante respecto a la nave, v0. Si la nave parte del reposo, ¿cuál será su velocidad cuando se le agote el combustible?
con una velocidad constante respecto a la nave, v0. Si la nave parte del reposo, ¿cuál será su velocidad cuando se le agote el combustible?
2.14 Colisión de dos péndulos
Se tienen dos péndulos ideales con barras rígidas de la misma longitud L y masa nula, que cuelgan del mismo punto O. Las masas sujetas a los extremos de los hilos son respectivamente m1 y m2. La masa m1 es elevada a una altura h1 y se suelta desde el reposo, colisionando con la masa m2 que se encuentra en el punto más bajo.
Suponiendo que la colisión es elástica, determina la altura a la que sube cada masa tras la colisión. Distingue los casos m1 > m2, m1 = m2 y m1 < m2.
¿Qué condiciones deben cumplirse para conseguir que la masa m2 gire y llegue hasta arriba del todo?
2.15 Granada en movimiento vertical
Una granada de masa M se lanza verticalmente desde el suelo con una velocidad de módulo v0. Se mueve sometida únicamente a la acción de la gravedad. En el punto más alto de la trayectoria la granada explota en dos trozos con la misma masa. Justo después de la explosión uno de los trozos se mueve verticalmente hacia arriba con una velocidad de módulo v1. Determina la velocidad en ese instante del otro trozo.
2.16 Intercambio de posiciones en una barca
Una barca de longitud 2L y masa mb = 3m0 está en reposo sobre el agua. En el extremo izquierdo de la barca se encuentra una persona de masa m1 = 2m0. En el extremo derecho hay otra persona de masa m2 = m0. Las dos personas intercambian sus posiciones caminando sobre la barca hacia el extremo opuesto. Si se desprecian las fuerzas que ejerce el agua sobre la barca, ¿cuanto se ha desplazado la barca y hacia donde?